Interference na planparalelní desce
Úloha číslo: 1562
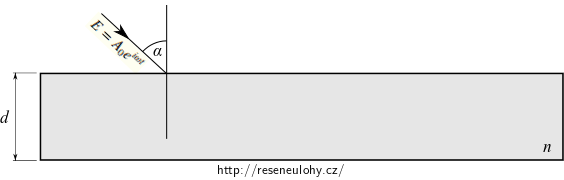
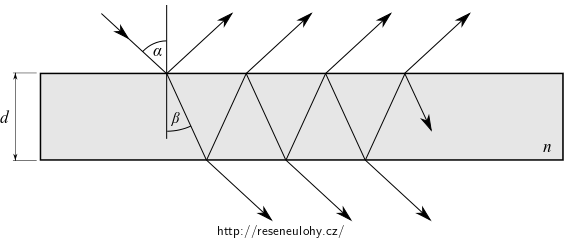
Na planparalelní desku tloušťky \(d\) o indexu lomu \(n\) dopadá ze vzduchu rovinná monochromatická vlna pod úhlem \(\alpha\). Vlna se částečně láme. Při mnohonásobném vnitřním odrazu vznikají lomem do vzduchu dvě soustavy koherentních vlnění, postupujících jednak ve směru původní dopadající vlny, jednak ve směru odraženého paprsku.
Určete, jaký podíl intenzity dopadnutého světla představuje intenzita světla
- odraženého od desky vzhůru,
- procházejícího na druhou stranu desky ve směru primární dopadající vlny.
Zkoumejte především závislost na vlnové délce \(\lambda\) dopadající vlny.
Pracujte s komplexními funkcemi. Uvažujte lineárně polarizovanou vlnu, jejíž kmitová rovina je buď totožná s rovinou dopadu nebo je k ní kolmá. Za místo superpozice volte bod dostatečně vzdálený od desky a desku uvažujte dostatečně rozlehlou.
Rozbor a teorie
Co se tu vlastně děje? Rovinná vlna se při dopadu na každé rozhraní vždy dělí na vlnu odraženou a lomenou. Výsledkem je vícenásobný odraz a lom uvnitř desky, který dává vzniku dvou systémů vln – vln deskou procházivších a vln postupujících zpět ve směru vlny odražené. Vlny v rámci systémů interferují a naším cílem je zjistit, na čem a jak výsledek interference závisí.
• Dopadne-li rovinná vlna s amplitudou elektrické intenzity \(E\) na rovinné rozhraní dvou prostředí, rozdělí se na dvě rovinné vlny – odraženou s amplitudou \(E^\mathcal{R}\) (reflexe) a lomenou s amplitudou \(E^\mathcal{T}\) (transmise) pro které platí
\[ \begin{eqnarray} E^\mathcal{R} &=& \sqrt{R} E,\\ E^\mathcal{T} &=& \sqrt{T} E, \end{eqnarray} \]kde \(\sqrt{R}\) je koeficient odrazivosti a \(\sqrt{T}\) koeficient propustnosti.
Tyto koeficienty závisejí na úhlu dopadu \(\alpha\) a indexech lomu obou prostředí. Složka elektrické intenzity dopadající vlny rovnoběžná s rovinou dopadu a složka k ní kolmá se chovají vzájemně nezávisle, vztahy pro amplitudy by bylo nutné obecně psát pro obě složky zvlášť. Tomu se vyhneme tím, že budeme uvažovat dopadající vlnu lineárně polarizovanou speciálně v jedné z těchto rovin.
• Veličiny \(R,T\) značí odrazivost a propustnost materiálu a mají význam poměrů intenzit světla odraženého (resp. lomeného) ku dopadajícímu. Jedná se tedy o podíl energetických veličin a platí
\[R+T=1.\]• Pro první odraz nutno přihlédnout ke změně fáze o \(\pi\), neboť jde o odraz od opticky hustšího prostředí.
• Projde-li světlo izotropním prostředím o indexu lomu \(n\) dráhu \(l\), změní se jeho fáze o
\[\delta = {\omega}{t} = \frac{2\pi}{T}\frac{l}{v} = \frac{2\pi}{T}\frac{nl}{c} = \frac{2\pi}{T}\frac{nlT}{\lambda} = \frac{2\pi}{\lambda}nl = knl.\]• Obecný tvar rovinné harmonické monochromatické vlny (komplexní formalismus) je
\[ \vec{E} = \vec{E_0} e^{i(\omega t - \vec{k}\cdot\vec{r} + \varphi )}, \] Pro naše účely postačí pracovat pouze s velikostí vektorů elektrické intenzity, navíc vynecháme prostorový člen \(\vec{k}\cdot\vec{r}\), zkrátka budeme interferenci sledovat v nějakém libovolném konkrétním místě \[ E = E_0 e^{i(\omega t + \varphi )}. \] Jednotlivé interferované vlny se budou lišit velikostí amplitudy (zmenšování koeficienty propustnosti a odrazivosti) a fází (odraz na opticky hustším prostředí + různé dráhy při různě násobných odrazech).• Za intenzitu světla budeme považovat střední hodnotu velikosti Poyntingova vektoru. Pro rovinnou vlnu lze vypočítat ze vztahu
\[ I = \frac{1}{2z_0} EE^\star, \] kde \(z_0\) je impedance vakua (vzduch z tohoto hlediska pokládejme za vakuum).a) Nápověda 1 – elektrická intenzita
Určete výrazy pro elektrickou intenzitu první, druhé až \(j\)-té z desky vzhůru vystupující rovinné vlny.
a) Nápověda 2 – výsledná elektrická intenzita
Nalezněte elektrickou intenzitu výsledné vlny, která vznikne interferencí \(E_1^\mathcal{R}, E_2^\mathcal{R},E_3^\mathcal{R},\dots\)
a) Nápověda 3 – intenzita světla
Určete intenzitu světla rovinné vlny vzniklé interferencí jednotlivých vzhůru odražených vln.
a) Nápověda 4 – podíl intenzit odraženého a dopadnutého světla
Vypočítejte intenzitu světla dopadající vlny a určete podíl intenzit světla odražené a dopadající vlny. Takto určenou relativní intenzitu vykreslete jako funkci vlnové délky \(\lambda\) použitého světla.
Odvození fázového zpoždění φ
Za pomoci trochy geometrie odvodíme vyjádření pro fázové zpoždění \(\varphi\) dvou po sobě vzniklých vln.
Na následujícím obrázku máme dva paprsky – paprsek vlny odražené ihned a vlny, která absolvovala uvnitř desky jeden odraz.
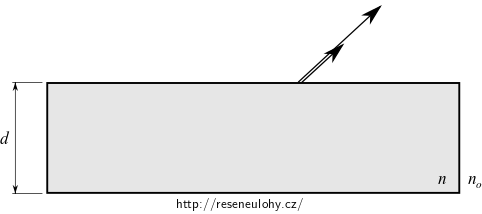
Dokresleme zpětně cestu těchto paprsků:
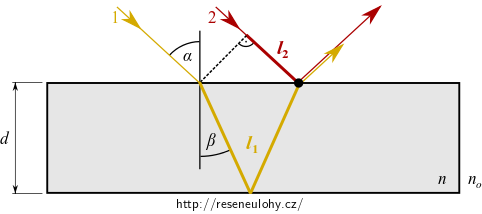
• Čárkovanou čarou jsme označili část vlnoplochy dopadající vlny – zde byly oba paprsky ještě ve fázi.
• Černý puntík je umístěn v bodě, od kterého se již rozdíl fází obou vln dále nemění.
Fázový rozdíl paprsků mezi těmito dvěma místy je
\[ \varphi = \varphi_1 - \varphi_2 = knl_1 - kn_0l_2, \tag{D.1}\]kde \(l_1, l_2\) jsou geometrické dráhy paprsků (vykresleny tučně), \(k\) velikost vlnového vektoru ve vakuu a \(n_\mathcal{o}\) index lomu okolního prostředí.
Dráhy \(l_1, l_2\) se nyní pokusíme vyjádřit pouze pomocí \(n, d, \beta\).
Paprsek 1 – vyjádření \(l_1\)
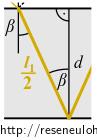
\[\hspace{-5em}\cos\beta = \frac{d}{\frac{l_1}{2}} \qquad \Rightarrow \qquad l_1 = \frac{2d}{\cos\beta}\tag{D.2}\] Paprsek 2 – vyjádření \(l_2\)
Dosadíme nalezená vyjádření (D.2), (D.3) do (D.1) \[ \varphi = k(nl_1 - n_\mathcal{o} l_2) = k \left( n\frac{2d}{\cos\beta} - n_\mathcal{o} 2d\mathrm{tg}\,\beta \sin\alpha \right) = \] za \(\sin\alpha\) dosadíme ze zákona lomu \(\frac{n}{n_\mathcal{o}}\sin\beta\) a upravíme \[ = k \left( n \frac{2d}{\cos\beta} - n_\mathcal{o} 2d \frac{\sin\beta}{\cos\beta} \frac{n}{n_\mathcal{o}} \sin\beta \right) = kn2d \left( \frac{1-\sin^2 \beta}{\cos \beta} \right) = kn2d\cos\beta. \]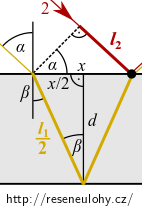
\[\hspace{-5em} \left. \begin{array}{ll} \sin\alpha = \frac{l_2}{x} & \quad\Rightarrow\quad & l_2 = x \sin\alpha \\ \mathrm{tg}\,\beta = \frac{x/2}{d} & \quad\Rightarrow\quad & x = 2d\,\mathrm{tg}\, \beta \end{array} \quad \right\} \quad l_2 = 2d\, \mathrm{tg}\,\beta \sin\alpha \tag{D.3}\] Vyjádřením velikosti vlnového vektoru \(k\) jako \(\frac{2\pi}{\lambda}\) dostáváme konečný vztah
\[ \varphi = \frac{4\pi}{\lambda}nd\cos\beta. \tag{D.4}\]• Reprezentuje-li paprsek 2 přímo odraženou vlnu a jde-li o odraz na opticky hustším prostředí, přičítá se navíc změna fáze o \(\pi\).
• Uvědomte si, že \(n\) odrazů uvnitř desky znamená fázové zpoždění vzhledem k první odražené vlně \(n\varphi\).
• Rozvažte, že právě vypočítané fázové zpoždění \(\varphi\) je stejné jako fázové zpoždění mezi vlnami systému vln vycházejících z desky směrem dolů (tj. úloha b).
b) Nápověda 1 – výpočet pro procházející světlo
Proveďte analogický výpočet jako v části a) pro světlo, které prochází deskou dolů.
CELKOVÉ ŘEŠENÍ
• Při dopadu rovinné vlny na rovinné rozhraní dvou prostředí se část vlny odrazí a část projde.
Pro odraženou vlnu platí \( \begin{eqnarray} E^\mathcal{R} &=& \sqrt{R} E,\end{eqnarray}\)
Pro lomenou vlnu platí \(\begin{eqnarray} E^\mathcal{T} &=& \sqrt{T} E,\end{eqnarray}\)
kde \(\sqrt{R}\) je koeficient odrazivosti a \(\sqrt{T}\) koeficient propustnosti.Veličiny \(R,T\) mají význam poměrů intenzit světla odraženého (resp. lomeného) ku dopadajícímu. Závisí na úhlu dopadu \(\alpha\) a indexech lomu obou prostředí. Zároveň pro ně platí \(R+T=1.\)
• Při prvním odrazu musíme počítat se změnou fáze o \(\pi\), neboť jde o odraz od opticky hustšího prostředí.
• Projde-li světlo izotropním prostředím o indexu lomu \(n\) dráhu \(l\), změní se jeho fáze o
\[\delta = {\omega}{t} = \frac{2\pi}{T}\frac{l}{v} = \frac{2\pi}{T}\frac{nl}{c} = \frac{2\pi}{T}\frac{nlT}{\lambda} = \frac{2\pi}{\lambda}nl = knl.\]• Pro jednoduchost budeme interferenci sledovat v nějakém libovolném konkrétním místě, a tak z obecného tvaru rovinné harmonické monochromatické vlny můžeme vynechat prostorový člen \(\vec{k}\cdot\vec{r}\). Tím dostáváme výraz pro rovinnou harmonickou monochromatickou vlnu ve tvaru
\[ E = E_0 e^{i(\omega t + \varphi )}. \]Jednotlivé interferované vlny se budou lišit velikostí amplitudy (zmenšování koeficienty propustnosti a odrazivosti) a fází (odraz na opticky hustším prostředí + různé dráhy při různě násobných odrazech).
• Za intenzitu světla budeme považovat střední hodnotu velikosti Poyntingova vektoru. Pro rovinnou vlnu lze vypočítat ze vztahu
\[ I = \frac{1}{2z_0} EE^\star, \]kde \(z_0\) je impedance vakua (vzduch z tohoto hlediska pokládejme za vakuum).
Nejprve určíme výrazy pro elektrickou intenzitu první až j-té z desky vzhůru vystupující rovinné vlny.
Nechť na desku dopadá rovinná vlna, která má ve zvoleném místě rozhraní průběh
\[E=A_0 e^{i\omega t}.\]Při dopadu na rozhraní vznikne odražená vlna s amplitudou \(\sqrt{R}A_0\) a s opačnou fází (odraz od opticky hustšího prostředí)
\[ E_1^\mathcal{R} = \sqrt{R}A_0 e^{i(\omega t + \pi)}. \]Dále bude pokračovat vlna lomená s amplitudou \(\sqrt{T}A_0\), směřující na spodní rozhraní.
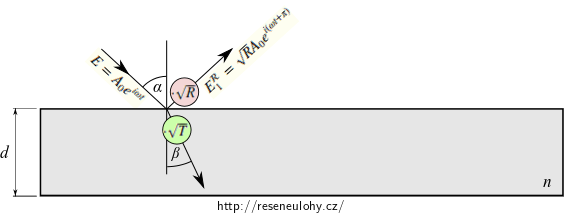
Po dopadu na dolní rozhraní se vlna současně lomí ven z desky a odráží se zpět.
Odražená vlna s amplitudou \(\sqrt{R}\sqrt{T}A_0\) směřuje k hornímu rozhraní, kde se znovu odráží a lomí, lomená vlna vystupuje z desky s amplitudou \(\sqrt{T} \sqrt{R} \sqrt{T} A_0\) a fázovým zpožděním \(\varphi = \frac{4\pi}{\lambda} n d\cos\beta\) vzhledem k předchozí odražené vlně těsně před odrazem (odvození fázového rozdílu zde). Tedy
\[ E_2^\mathcal{R} = \sqrt{T} \sqrt{R} \sqrt{T} A_0 e^{i(\omega t + \varphi)}. \]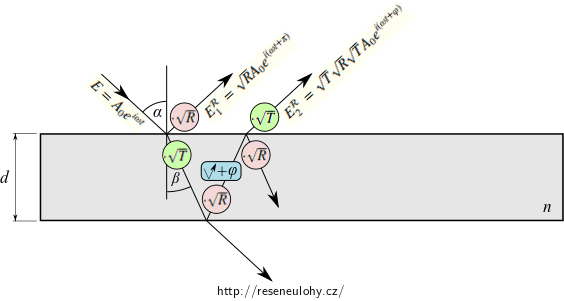
Každá následující z desky vzhůru vystupující vlna absolvuje oproti té předchozí o dva odrazy více a získá další fázové zpoždění o velikosti \(\varphi\), tj.
\[ E_3^\mathcal{R} = \sqrt{T} \sqrt{R} \sqrt{R} \sqrt{R} \sqrt{T} A_0 e^{i(\omega t + 2\varphi)}, \] \[ E_4^\mathcal{R} = \sqrt{T} \sqrt{R} \sqrt{R} \sqrt{R} \sqrt{R} \sqrt{R} \sqrt{T} A_0 e^{i(\omega t + 3\varphi)}. \]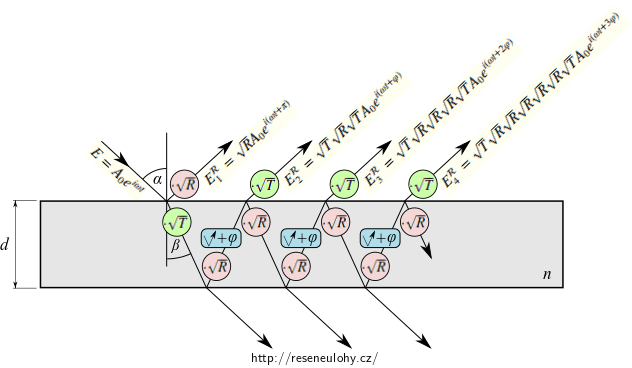
Tedy \(j\)-tá vlna
\[ E_j^\mathcal{R} = T R^{j-2} \sqrt{R} A_0 e^{i\left[\omega t + (j-1)\varphi\right]}, \quad \text{pro}\ j=2{,}3,\dots \]Nyní nalezneme elektrickou intenzitu výsledné vlny, která vznikne interferencí \(E_1^\mathcal{R}, E_2^\mathcal{R},E_3^\mathcal{R},\dots\)
K nalezení elektrické intenzity výsledné vlny šířící se zpět od desky je potřeba sečíst elektrické intenzity všech vzhůru vystupujících vln.
Tedy
\[ E^\mathcal{R} = \sum_{j=1}^{\infty} E_j^\mathcal{R} = \sqrt{R}A_0 e^{i(\omega t + \pi)} + \sum_{j=2}^{\infty} T R^{j-2} \sqrt{R} A_0 e^{i\left[\omega t + (j-1)\varphi\right]}= \] \[ = \sqrt{R}A_0 e^{i(\omega t + \pi)} + T \sqrt{R} A_0 e^{i\omega t} \sum_{j=2}^{\infty} R^{j-2}e^{i(j-1)\varphi}= \]Onu nekonečnou řadu umíme sečíst, jde o geometrickou řadu s prvním členem \(e^{i\varphi}\) a kvocientem \(Re^{i\varphi}\) (jistě je \(|Re^{i\varphi}|\lt 1\)), tedy
\[ \color{MidnightBlue}{ \sum_{j=2}^{\infty} R^{j-2}e^{i(j-1)\varphi} = e^{i\varphi} \frac{1}{1-Re^{i\varphi}}. } \]Dosadíme součet geometrické řady a upravíme (\(\small e^{i\pi} = \cos \pi + i\sin\pi = -1\)).
\[ = \sqrt{R}A_0 e^{i(\omega t + \pi)} + T \sqrt{R} A_0 e^{i\omega t} e^{i\varphi} \frac{1}{1-Re^{i\varphi}} = A_0 \sqrt{R} e^{i\omega t} \left( \underbrace{e^{i\pi}}_{-1} + \frac{T e^{i\varphi}}{1-Re^{i\varphi}} \right) = \] \[ = A_0 \sqrt{R} e^{i\omega t} \frac{T e^{i\varphi} -1 + Re^{i\varphi} }{1-Re^{i\varphi}} = A_0 \sqrt{R} e^{i\omega t} \frac{\overbrace{(T+R)}^{1}e^{i\varphi} -1 }{1-Re^{i\varphi}}, \] čímž dostáváme konečný výraz pro elektrickou intenzitu odražené vlny \[ E^\mathcal{R} = A_0 \sqrt{R} e^{i\omega t} \frac{e^{i\varphi} -1 }{1-Re^{i\varphi}}. \]Dále určíme intenzitu světla rovinné vlny vzniklé interferencí jednotlivých vzhůru odražených vln.
Do vztahu pro intenzitu světla rovinné vlny dosadíme již odvozený vztah pro elektrickou intenzitu rovinné vlny a upravíme
\[ I^\mathcal{R} = \frac{1}{2z_0} E^\mathcal{R} {{E}^\mathcal{R}}^\star = \frac{A_0^2 R}{2z_0}\underbrace{e^{i\omega t} e^{-i\omega t}}_{1} \frac{(e^{i\varphi}-1)(e^{-i\varphi}-1)}{(1-Re^{i\varphi})(1-Re^{-i\varphi})}= \frac{A_0^2 R}{2z_0} \frac{\overbrace{e^{i\varphi}e^{-i\varphi}}^{1} - e^{i\varphi} - e^{-i\varphi} + 1}{1 - Re^{-i\varphi} - Re^{i\varphi} + \underbrace{Re^{i\varphi}Re^{-i\varphi}}_{R^2}}= \]\[ =\frac{A_0^2 R}{2z_0} \frac{ 2 - \overbrace{(e^{i\varphi} + e^{-i\varphi}}^{2\cos\varphi})}{1 + R^2 - R\underbrace{(e^{i\varphi}+e^{-i\varphi})}_{2\cos\varphi}}= \frac{A_0^2 R}{2z_0} \frac{ 2 - 2\cos\varphi}{1 + R^2 - 2R\cos\varphi}= \] v čitateli využijeme vzorec výše a ve jmenovateli doplníme na čtverec a dostáváme \[ = \frac{A_0^2 R}{2z_0} \frac{2(1 - \cos\varphi)}{T^2 + 2R(1 - \cos\varphi)}. \]Dale v úpravách použijeme vzorec
\[ \small \color{MidnightBlue}{ e^{i\varphi} + e^{-i\varphi} = \cos \varphi + i\sin\varphi + \cos\varphi - i\sin\varphi = 2\cos\varphi. } \]Nakonec použijeme goniometrický vzorec \(\small \frac{1-\cos\alpha}{2} = \sin^2 \frac{\alpha}{2}\) a dostáváme hledanou intenzitu ve tvaru
\[ I^\mathcal{R} = \frac{A_0^2 R}{2z_0} \frac{4\sin^2 \frac{\varphi}{2}}{T^2 + 4R\sin^2 \frac{\varphi}{2} }. \]Vypočítáme intenzitu světla dopadající vlny a určíme podíl odražené a dopadající vlny.
Intenzita světla dopadající vlny \(E=A_0 e^{i\omega t}.\) je
\[ I_0 = \frac{A_0^2}{2z_0}. \]Hledaný podíl intenzit světla odražené a dopadající vlny je tedy
\[ \frac{I^\mathcal{R}}{I_0} = \frac{\frac{A_0^2}{2z_0} R \frac{4\sin^2 \frac{\varphi}{2}}{T^2 + 4R\sin^2 \frac{\varphi}{2}}}{\frac{A_0^2}{2z_0}}= \frac{4R\sin^2 \frac{\varphi}{2}}{T^2 + 4R\sin^2 \frac{\varphi}{2}}, \quad \text{kde } \varphi = \frac{4\pi n d}{\lambda}\cos \beta. \]Odvození fázového zpoždění \(\varphi\) je uvedeno v oddělené sekci výše.
♣ Tento podíl vyjadřuje, jaká část světla se z energetického hlediska odráží od desky zpět. Budeme jí proto říkat odrazivost planparalelní desky.
♣ Vidíme, že odrazivost desky závisí na odrazivosti \(R\) (a tedy i propustnosti \(T\)) daného materiálu, na indexu lomu \(n\) a tloušťce \(d\) vrstvy, na úhlu lomu \(\beta\) a vlnové délce \(\lambda\).
♣ Následující graf znázorňje závislost odrazivosti planparalelní desky \(\frac{I^\mathcal{R}}{I_0}\) na vlnové délce \(\lambda\), přičemž uvažujeme kolmý dopad (\(\beta=0^\mathrm{\circ}\)) na vrstvy s tloušťkou \(d=1\,\mathrm{\mu m}\) s různými odrazivostmi materiálu: \(R=0{,}98\) (chování zrcadla), \(R=0{,}5\) (přibližně germanium) a \(R=0{,}04\) (obyčejné sklo).
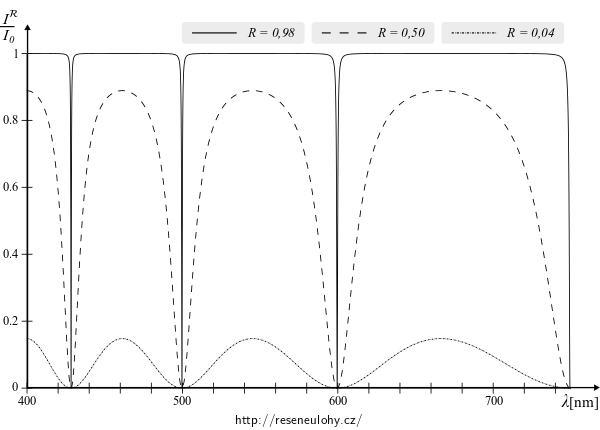
Vidíme, že zrcadlo odráží všechny vlnové délky téměř \(100\%\), zatímco skleněná destička odráží mnohem méně. V každém případě je však na určitých vlnových délkách odražená intenzita maximální. Právě tento jev stojí za duhovým zbarvením olejových skvrn na kalužích, mydlinkových bublin, ochranných vrstev brýlí a objektivů, jsou-li osvětleny bílým světlem.
Zajímavá je i závislost na tloušťce vrstvy. Vykresleme nyní graf pro desetkrát silnější vrstvu, tedy \(10\,\mathrm{\mu m}\).
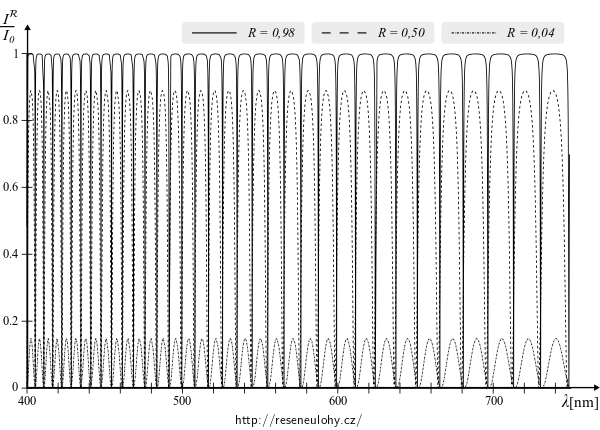
Pokud zvětšujeme tloušťku vrstvy, graf se zahušťuje – maxima intenzity dosahuje čím dál více vlnových délek blíže sobě, čímž vrstva postupně ztrácí na zajímavosti. Pro vrstvu silnou \(1\,\mathrm{mm}\) by nám graf elegantně „vyčernil“ obdelníček. Můžete si například dát několik tenkých sklíček na sebe a uvidíte, že čím víc jich budete mít na sobě tím víc se světlo bude odrážet.
Nyní budeme řešit část úloh b) pro procházející světlo.
Řešení bude analogické s řešení části a).
První z desky vystupující rovinná vlna má ve zvoleném místě rozhraní průběh
\[E^\mathcal{T}_1= \sqrt{T}\sqrt{T} A_0 e^{i\omega t}.\]Každá další vlna z desky vystupující absolvuje oproti předchozí vlně o dva odrazy více a získá fázový rozdíl \(\varphi\), tj.
\[ \begin{eqnarray} E^\mathcal{T}_1 &=& \sqrt{T}\sqrt{T} A_0 e^{i\omega t}\\ E_2^\mathcal{T} &=& \sqrt{T} \sqrt{R}\sqrt{R} \sqrt{T} A_0 e^{i(\omega t + \varphi)} \\ E_3^\mathcal{T} &=& \sqrt{T} \sqrt{R} \sqrt{R} \sqrt{R} \sqrt{R} \sqrt{T} A_0 e^{i(\omega t + 2\varphi)} \\ \vdots &\phantom{=}& \vdots \\ E_j^\mathcal{T} &=& T R^{j-1} A_0 e^{i\left[\omega t + (j-1)\varphi\right]}\\ \vdots &\phantom{=}& \vdots \end{eqnarray} \]Elektrická intenzita výsledné vlny je součtem příspěvků všech vzniklých vln, tedy
\[ E^\mathcal{T} = \sum_{j=1}^{\infty} E_j^\mathcal{T} = \sum_{j=1}^{\infty} T R^{j-1} A_0 e^{i\left[\omega t + (j-1)\varphi\right]} = T A_0 e^{i\omega t} \sum_{j=1}^{\infty} R^{j-1} e^{i(j-1)\varphi} = T A_0 e^{i\omega t} \frac{1}{1 - R\,e^{i\varphi}}. \]Určíme intenzitu světla
\[ I^\mathcal{T} = \frac{1}{2z_0} E^\mathcal{T} {E^\mathcal{T}}^\star = \frac{1}{2z_0} T^2 A_0^2\, \underbrace{e^{i\omega t}e^{-i\omega t}}_{1} \frac{1}{1 - R\,e^{i\varphi}} \frac{1}{1 - R\,e^{-i\varphi}} = \frac{1}{2z_0} A_0^2 \frac{T^2}{1 - R\,e^{i\varphi} - R\,e^{-i\varphi} + R^2} = \] \[ = \frac{1}{2z_0} A_0^2 \frac{T^2}{1 - 2R\cos\varphi + R^2} = \frac{1}{2z_0} A_0^2 \frac{T^2}{(1 - R)^2 + 2R - 2R\cos\varphi} = \] \[ = \frac{1}{2z_0} A_0^2 \frac{T^2}{T^2 + 2R(1 - \cos\varphi)} = \frac{1}{2z_0} A_0^2 \frac{T^2}{T^2 + 4R \sin^2 \frac{\varphi}{2}}. \]Hledaný podíl intenzit světla pošlé a dopadající vlny tedy je
\[ \frac{I^\mathcal{T}}{I_0} = \frac{\frac{1}{2z_0} A_0^2 \frac{T^2}{T^2 + 4R \sin^2 \frac{\varphi}{2}}}{\frac{1}{2z_0}A_0^2} = \frac{T^2}{T^2 + 4R \sin^2 \frac{\varphi}{2}}, \quad \text{kde } \varphi = \frac{4\pi n d}{\lambda}\cos \beta. \]♣ Tento podíl vyjadřuje, jaká část světla z energetického hlediska deskou prochází. Budeme jí proto říkat propustnost planparalelní desky.
Podíly intenzit celkového odraženého světla a celkového procházejícího světla ku intenzitě dopadající vlny by měly v součtu dát jedničku. Opravdu
\[ \frac{I^\mathcal{R}}{I_0} + \frac{I^\mathcal{T}}{I_0} = \frac{4R\sin^2\frac{\varphi}{2}}{T^2 + 4R \sin^2 \frac{\varphi}{2}} + \frac{T^2}{T^2 + 4R \sin^2 \frac{\varphi}{2}} = 1. \]To znamená, že propustnost je vidět přímo v grafu odrazivosti desky – je doplňkem funkčních hodnot do jedničky.

Odpověď
a) Podíl intenzit odraženého a dopadajícího světla je
\[\frac{I^\mathcal{R}}{I_0} = \frac{4R\sin^2 \frac{\varphi}{2}}{T^2 + 4R\sin^2 \frac{\varphi}{2}}, \quad \text{kde } \varphi = \frac{4\pi n d}{\lambda}\cos \beta.\]b) Podíl intenzit procházejícího a dopadajícího světla je
\[\frac{I^\mathcal{T}}{I_0} = \frac{T^2}{T^2 + 4R\sin^2 \frac{\varphi}{2}}, \quad \text{kde } \varphi = \frac{4\pi n d}{\lambda}\cos \beta.\]Závislost odrazivosti planparalelní desky \(\frac{I^\mathcal{R}}{I_0}\) o tloušťce \(d=1\,\mathrm{\mu m}\) na vlnové délce \(\lambda\) pro různé hodnoty odrazivosti \(R\) materiálu desky:

Hodnoty propustnosti planparalelní desky \(\frac{I^\mathcal{T}}{I_0}\) jsou doplňky vykreslených funkčních hodnot do jedničky.