Loděnka a dírková komora
Úloha číslo: 1914

V Tichém oceánu najdeme velmi zajímavé živočichy. Jedním z nich je loděnka. Jedná se o hlavonožce s ulitou, která se dá matematicky popsat jako logaritmická spirála.
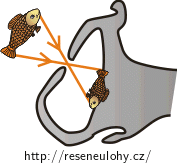
Víte jak funguje dírková komora (nazývaná také „camera obscura“)? Zkuste vyřešit následující problém.
Zapalená svíčka, jejíž plamen má výšku \(1 \mathrm{cm}\), se nachází ve vzdálenosti \(20 \mathrm{cm}\) od krabice, která funguje jako dírková komora.
a) Jakou výšku bude mít obraz plamene, který dírková komora vytvoří na zadní stěně krabice? Vzdálenost mezi přední stěnou krabice, ve které je malá dírka, a zadní stěnou krabice je \(40 \mathrm{cm}\).
Jak by se tato výška změnila, pokud by svíčka byla ve vzdálenosti b) \(10 \mathrm{cm}\) či c) \(30 \mathrm{cm}\) od krabice?
Zápis
\(h_{p}=1 \mathrm{cm}\) výška plamene svíčky \(x=40 \mathrm{cm}\) vzdálenost mezi přední a zadní stěnou krabice \(l_{a}=20 \mathrm{cm}\) vzdálenost mezi svíčkou a krabicí v případě a) \(h_{oa}= ?\) výška obrazu plamene svíčky v případě a) \(l_{b}=10 \mathrm{cm}\) vzdálenost mezi svíčkou a krabicí v případě b) \(h_{ob}= ?\) výška obrazu plamene svíčky v případě b) \(l_{c}=30 \mathrm{cm}\) vzdálenost mezi svíčkou a krabicí v případě c) \(h_{oc}= ?\) výška obrazu plamene svíčky v případě c) Nápověda 1
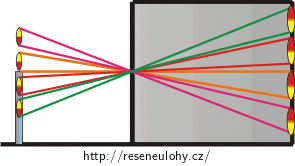
Zakreslete zobrazení plamene svíčky pomocí dírkové komory do obrázku. Vytvořený obrázek popište. Pokud nevíte, jakým způsobem zobrazuje dírková komora předměty, pečlivě si prohlédněte zadání, kde naleznete nápovědu. Předpokládejte, že dírka v dírkové komoře je velmi malá a můžeme ji proto považovat za bod.
Nápověda 2
V obrázku z předchozí nápovědy můžeme najít dva trojúhelníky.
Co mají společného?
Nápověda 3
Užitím podobnosti trojúhelníků určete výšku obrazu plamene.
Celkové řešení
Budeme předpokládat, že dírku můžeme považovat za bod.
Výška, v jaké se nachází plamen svíčky, ani výška, ve které je dírka dírkové komory, nemají na řešení úlohy žádný vliv a můžeme si je zvolit libovolně. Abychom si ulehčili práci při dalším postupu, umístíme plamen tak, aby jeden z paprsků, který dopadá z jeho počátku či vrcholu, byl vodorovný.
V tomto obrázku jsou pro nás užitečné dva trojúhelníky (jsou zvýrazněny modrou a žlutou barvou).
Z geometrie víme, že modrý a žlutý trojúhelník se shodují ve fialově vyznačeném úhlu (tzv. vrcholové úhly). Dále se v obou případech jedná o pravoúhlý trojúhelník.Když se dva trojúhelníky shodují ve dvou úhlech, pak jsou podobné.
Pro podobné trojúhelníky platí, že se shodují poměry odpovídajících si stran:
\[\frac{h_{oa}}{h_{p}}=\frac{x}{l_{a}}.\]
Obě strany rovnice vynásobíme \(h_{p}\) a tím získáme hledaný vztah pro výšku obrazu plamene:
\[h_{oa}=h_{p}\frac{x}{l_{a}}.\]
Číselné řešení
Ze zadání víme:
\(h_{p}=1 \mathrm{cm}\)
\(x=40 \mathrm{cm}\)
Dosadíme:
a) \(l_{a}=20 \mathrm{cm}\)
\(h_{oa}=h_{p}\frac{x}{l_{a}}=1\cdot \frac{40}{20} \mathrm{cm}=2 \mathrm{cm}.\)
Obraz plamene bude dvakrát vyšší než zobrazovaný plamen.
Nyní dopočítáme, jak se výška obrazu změní, pokud se změní vzdálenost plamene svíčky od dírkové komory.
Dosadíme:
b) \(l_{b}=10 \mathrm{cm},\)
\(h_{ob}=h_{p}\frac{x}{l_{b}}=1\cdot \frac{40}{10} \mathrm{cm}=4 \mathrm{cm}.\)
Obraz plamene bude čtyřikrát vyšší než zobrazovaný plamen.
c) \(l_{1c}=30 \mathrm{cm},\)
\(h_{oc}=h_{p}\frac{x}{l_{c}}=1\cdot \frac{40}{30} \mathrm{cm}=\frac{4}{3} \mathrm{cm} \dot= 1{,}3 \mathrm{cm}\).
Obraz plamene bude \(1{,}3\) krát vyšší než zobrazovaný plamen.
Z podobnosti trojúhelníků a ze získaných výsledků můžeme vypozorovat, že obraz plamene je stejně vysoký jako jeho vzor, pokud je vzdálenost plamene od krabice stejná jako vzdálenost přední a zadní stěny krabice. Navíc si můžeme všimnout, že když zvětšíme vzdálenost plamene od krabice n-krát, tak se obraz plamene n-krát zmenší. Když tuto vzdálenost naopak n-krát zmenšíme, tak se obraz plamene n-krát zvětší. Mezi výškou obrazu plamene a vzdáleností plamene od krabice platí nepřímá úměrnost.
Odpověď
Výška obrazu plamene bude \(h_{o}=2 \mathrm{cm}\).
Po změně vzdálenosti plamene od dírkové komory bude výška jeho obrazu:
a) \(h_{oa}=4 \mathrm{cm}\),
b) \(h_{ob}=\frac{4}{3} \mathrm{cm} \dot= 1{,}3 \mathrm{cm}\).
Vlastnosti dírkové komory
Obraz vytvořený dírkovou komorou má oproti běžné fotografii vytvořené fotoaparátem s objektivem určité výhody:
- zachovává perspektivu,
- blízké a daleké předměty jsou stejně ostré,
- její zobrazení pokryje velmi široký úhel.
Ale také nevýhody:
- nemožnost vyfotit pohybující se předměty,
- malá neostrost celého obrazu,
- fotografie je na okraji tmavší,
- je třeba zvolit vhodný průměr dírky. (Jak na to, se můžete dočíst zde: Výroba dírky)
Vysvětlení některých výše zmíněných bodů:
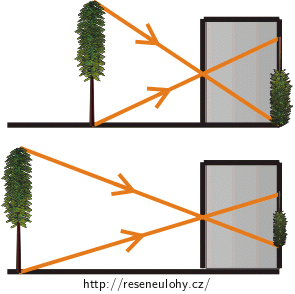
zachovává perspektivu:
Paprsky světla se přes dírkovou komoru šíří lineárně. Díky tomu bude např. pro stejně vysoké předměty postavené za sebou platit, že obraz předmětu který je blíže dírkové komoře, se bude jevit větší než obraz vzdálenějšího předmětu.
malá neostrost celého obrazu
Je způsobena tím, že bod je zobrazován jako kolečko.
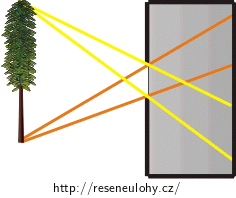
fotografie je na okraji tmavší:
To je způsobené tloušťkou materiálu kolem dírky. Prostředek fotografie je osvětlen více než okraje. Na obrázku můžeme vidět, kolik světla z jednotivých zobrazovaných bodů se dostane za štěrbinu. Čím bude materiál v okolí dírky tenčí, tím méně bude na okrajích fotografie docházet ke ztmavení.
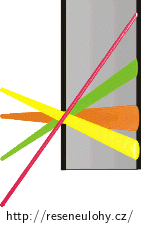
je třeba zvolit vhodný průměr dírky:
Obrázek ukazuje, že při použití velké dírky vzniká neostrost.
Obecně tedy platí, že čím menší dírka, tím je obraz ostřejší. Pokud je však dírka moc malá, začne docházet k ohybu světla, který způsobí, že ostrost bude menší.Zde jsme uvedli jen některé výhody a nevýhody dírkové komory. Podrobnější informace naleznete např. na Co je dírková komora .