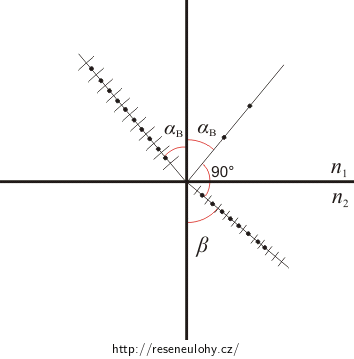Sbírka řešených úloh

Polarizace úplným odrazem

Úloha číslo: 1618

• Nápověda 1

  Jak funguje polarizace odrazem a jaký vztah platí pro tzv. Brewsterův úhel dopadu?

• Řešení nápovědy 1

  Pokud dopadá nepolarizované světlo na rozhraní dvou prostředí, dochází zde zároveň k odrazu a lomu. Pokud odražený a lomený paprsek svírají úhel 90°, je odražený paprsek úplně polarizován. Úhel dopadu, kdy je uvedená podmínka splněná, nazýváme Brewsterův úhel α_B, který závisí na indexu lomu prostředí.

  Poznámka: odražený paprsek je polarizován v rovině kolmé k rovině dopadu.

  

  Na obrázku je tečkami vyznačen směr kmitání v rovině kolmé k rovině dopadu a krátkými úsečkami je vyznačen směr kmitání v rovině dopadu.

  Jestliže odražený a lomený paprsek svírají úhel 90°, je možné získat z obrázku vztah:

  \[\alpha_\mathrm{B}+ 90° + \beta = 180°.\]

  Po úpravě dostaneme:

  \[\beta = 90° − \alpha_\mathrm{B}. \]

  Potom lze upravit Snellův zákon do tvaru:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\, \beta}=\frac{n_\mathrm{2}}{n_\mathrm{1}}.\]

  Po dosazení za β dostaneme:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\,(90° - \alpha_\mathrm{B})}=\frac{n_\mathrm{2}}{n_\mathrm{1}}.\]

  S využitím vlastností goniometrických funkcí sin(90° − α) = cos α lze předchozí vztah přepsat na:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\mathrm{tg}\,\, \alpha_\mathrm{B}=\frac{n_\mathrm{2}}{n_\mathrm{1}}\]

  a dostat vztah pro závislost Brewsterova úhlu α_B na indexech lomu obou prostředí.

• Řešení

  Odražené světlo je úplně polarizované jen při speciálním úhlu dopadu, tzv. Brewsterově úhlu α_B, při kterém odražený a lomený paprsek svírají úhel 90°. Je možné získat vztah:

  \[\alpha_\mathrm{B}+ 90° + \beta = 180°.\]

  Pro podrobné odvození se můžeme podívat do Řešení nápovědy 1.

  Po úpravě dostaneme:

  \[\beta = 90° − \alpha_\mathrm{B}. \]

  a upravíme Snellův zákon do tvaru:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\, \beta}=\frac{\sin\, \alpha_\mathrm{B}}{\sin\,(90° − \alpha_\mathrm{B})}=\frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\mathrm{tg}\,\, \alpha_\mathrm{B}= \frac{n_\mathrm{2}}{n_\mathrm{1}}.\]

  Protože nebylo v zadání řečeno jinak, předpokládejme, že vše se odehrává ve vakuu či vzduchu a můžeme dosadit n₁ = 1.

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}= \frac{n_\mathrm{2}}{1},\]

  tedy:

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}= n_\mathrm{2}.\]

  Ze zadání už můžeme dosadit Brewsterův úhel α_B = 58° a vypočítat index lomu emailu:

  \[n_\mathrm{2}=\mathrm{tg}\,\,58°\dot=\,1{,}6.\]

  Také už můžeme spočítat Brewsterův úhel pro diamant s indexem lomu n₂ = 2,42:

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}= n_\mathrm{2} = 2{,}42,\] \[\alpha_\mathrm{B} \dot=\,68°.\]

• Odpověď

  Index lomu emailu je n = 1,6 a polarizační úhel diamantu je α_B = 68°.