Vzdálenost knihy při čtení bez brýlí
Úloha číslo: 1906
Člověk používá brýle s čočkami o optické mohutnosti \(+2{,}75 \mathrm{D}\). V jaké vzdálenosti od očí by musel držet knihu, kdyby ji chtěl číst bez brýlí?
Zápis
\(φ= +2{,}75 \mathrm{D}\) optická mohutnost \(x= ?\) vzdálenost knihy od oka při čtení bez brýlí Nápověda 1
Jakou oční vadou náš člověk trpí? Jak se tato vada projeví, při čtení bez brýlí?
Co znamená pojem „konvenční zraková vzdálenost“?
Nápověda 2
Zamyslete se nad tím, jak dalekozrakému člověku pomohou brýle na čtení. Proč může s brýlemi číst text z kratší vzdálenosti?
Nápověda 3
Zobrazovací rovnice čočky nám říká, jaký je vztah mezi ohniskovou vzdáleností čočky a předmětovou a obrazovou vzdáleností. Předmětovou vzdálenost známe (\(a=d\)), obrazovou vzdálenost (\(a'=x\)) chceme vypočítat. Abychom úlohu mohli vyřešit, potřebujeme ještě zjistit, jaká je ohnisková vzdálenost brýlových čoček.
Napište zobrazovací rovnici a zamyslete se, jak spolu souvisí ohnisková vzdálenost \(f\) a optická mohutnost \(φ\). Následně určete hledanou vzdálenost \(x\).
Nápověda 4
Vyšlo nám, že \(x=−0{,}8 \mathrm{m}.\) Co nám říká znaménko „minus“?
Celkové řešení
Druh oční vady
Optická mohutnost čoček brýlí je kladná. To znamená, že čočky brýlí jsou spojky.
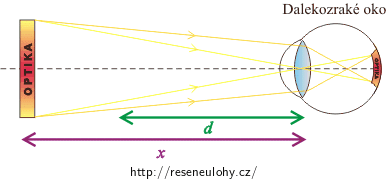
Z toho vyplývá, že náš člověk trpí dalekozrakostí. Dalekozraký člověk špatně vidí na blízko. Pokud chce číst bez brýlí, tak si musí knihu dát do větší vzdálenosti před sebe.
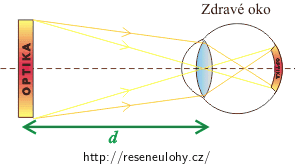
\(d\) značí konvenční zrakovou vzdálenost. Je to nejmenší vzdálenost, ze které člověk se zdravýma očima může číst delší dobu bez únavy (\(d=25 \mathrm{cm}\)).
Dalekozraký člověk s brýlemi
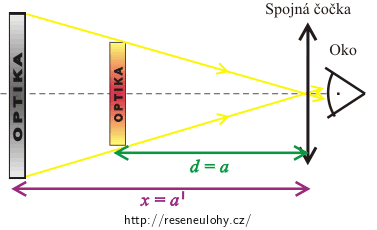
Člověk s brýlemi dobře uvidí i blízké předměty (předmět umístěný v konvenční zrakové vzdálenosti \(d\)). Brýlové čočky (spojné čočky) zobrazí blízké předměty do místa, odkud by je dobře viděl bez brýlí (pouhým okem). Tedy do vzdálenosti \(x\), kterou hledáme. Proto dalekozraký člověk, který nosí brýle, může číst text z kratší vzdálenosti.
\(a\) je předmětová vzdálenost a \(a'\) je obrazová vzdálenost.
Zobrazovací rovnice
Zobrazovací rovnice čočky nám říká, jaký je vztah mezi ohniskovou vzdáleností čočky a předmětovou a obrazovou vzdáleností. Předmětovou vzdálenost známe, obrazovou vzdálenost chceme určit. Abychom úlohu vyřešili, potřebujeme ještě zjistit, jaká je souvislost mezi ohniskovou vzdáleností brýlových čoček \(f\) a optickou mohutností \(φ\).
Napíšeme zobrazovací rovnici pro čočku: \[\frac{1}{f}=\frac{1}{a}+\frac{1}{a'}.\] Optická mohutnost odpovídá převrácené hodnotě ohniskové vzdálenosti: \[φ=\frac{1}{f}.\] Dosadíme do rovnice dle předchozího vztahu: \[φ=\frac{1}{a}+\frac{1}{a'}.\]
Protože z obrázku „Oko se spojnou čočkou“ víme, že platí \(a=d\) a \(a'=x\), můžeme tyto vztahy dosadit do rovnice: \[φ=\frac{1}{d}+\frac{1}{x}.\] Chceme vyjádřit \(x\). Obě strany rovnice vynásobíme výrazem \(dx\): \[φdx=x+d.\] Od obou stran rovnice odečteme \(x\): \[φdx−x=d.\] Vytkneme \(x\): \[x\left(φd−1\right)=d.\] Obě strany rovnice vydělíme výrazem \(φd−1\): \[x=\frac{d}{φd−1}.\]
Číselné řešení
Ze zadání víme:
\(φ= 2{,}75 \mathrm{D}\) (optická mohutnost)
V tabulkách dohledáme:
\(d= 0{,}25 \mathrm{m}\) (konvenční zraková vzdálenost)
Dosadíme:
\(x=\frac{d}{φd−1}=\frac{0{,}25}{2{,}75{\cdot}0{,}25−1} \mathrm{m}=−0{,}8 \mathrm{m}.\)
Znaménko „minus“
Vzdálenost \(x\) se rovná obrazové vzdálenosti \(a'\). Znaménko „minus“ před obrazovou vzdáleností nám říká, že obraz vzniká před čočkou brýlí. Knihu tedy musí člověk držet ve vzdálenosti \(0{,}8 \mathrm{m}\) před očima.
Poznámka: Při řešení úlohy jsme využili znaménkové konvence, která je uvedena v úloze Zobrazení netopýra kulovým zrcadlem a spojnou čočkou.
Odpověď
Při čtení bez brýlí by člověk musel držet knihu ve vzdálenosti \(0{,}8 \mathrm{m}\) před očima.
Odkaz na experiment
V Krátkozrakost a dalekozrakost naleznete experiment, který ukazuje, jak se dá korigovat krátkozrakost a dalekozrakost.