Sbírka řešených úloh

Ploskodutá čočka

Úloha číslo: 1918

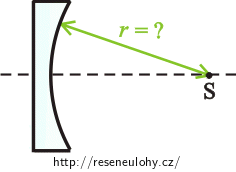
Ploskodutá čočka zhotovená ze skla o indexu lomu \(1{,}5\) je umístěna ve vzduchu. Její ohnisková vzdálenost je \(−10 \mathrm{cm}\). Určete její poloměr křivosti.

• Zápis

  \(n_{s}=1{,}5\)	index lomu skla
  \(f=10 \mathrm{cm}\)	ohnisková vzdálenost
  \(r= ?\)	poloměr křivosti

• Nápověda 1

  Každá čočka má dva poloměry křivosti. Proč v tomto případě hledáme hodnotu jen jednoho z nich?

• Řešení nápovědy 1

  Hodnotu poloměru křivosti ploské (první) plochy \(r_{1}\) známe, neboť se blíží k nekonečnu. To je důvod, proč hledáme pouze hodnotu poloměru křivosti duté (druhé) plochy \(r_{2}=r\).

• Nápověda 2

  Předpokládejme, že se jedná o tenkou čočku. Poloměry křivosti ovlivňují ohniskovou vzdálenost čočky. Dokážete tuto skutečnost popsat matematicky?

• Řešení nápovědy 2

  Změnu ohniskové vzdálenosti čočky \(f\) v závislosti na změně poloměrů křivosti optických ploch \(r_{1}\) a \(r_{2}\) popisuje zobrazovací rovnice. Napíšeme ji pro tenkou čočku. \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right),\] kde \(n_{s}\) je index lomu skla a \(n_{v}\) je index lomu vzduchu.

• Nápověda 3

  Jak upravíme zobrazovací rovnici, aby ohnisková vzdálenost byla závislá jen na jednom poloměru křivosti \(r_{2}=r\)? Následně tento poloměr vyjádřete a dopočítejte číselně.

• Řešení nápovědy 3

  Místo \(r_{2}\) budeme v zobrazovací rovnici psát \(r\): \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right),\] \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r}\right).\]

  Poloměr \(r_{1}\) se blíží k nekonečnu. Z toho plyne, že zlomek \(\frac{1}{r_{1}}\) se blíží k nule. Můžeme tedy psát:

  \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\left(0+\frac{1}{r}\right),\] \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\frac{1}{r}.\]

  Obě strany rovnice vynásobíme výrazem \(r\cdot f\): \[r=\left(\frac{n_{s}}{n_{v}}−1\right)f.\]

  Číselné řešení

  Ze zadání víme:

  \(n_{s}=1{,}5\) (index lomu skla)

  \(f=−10 \mathrm{cm}\) (ohnisková vzdálenost čočky)

  V tabulkách dohledáme hodnotu indexu lomu vzduchu:

  \(n_{v}=1{,}0\)

  Dosadíme:

  \(r=\left(\frac{n_{s}}{n_{v}}−1\right)f=\left(\frac{1{,}5}{1{,}0}−1\right)\cdot \left(−10\right) \mathrm{cm}=0{,}5\cdot \left(−10\right) \mathrm{cm}=−5 \mathrm{cm}.\)

• Poznámka

  Hodnota poloměru křivosti vyšla záporná, neboť se jedná o poloměr křivosti duté plochy (viz znaménková konvence uvedená v Zobrazení netopýra kulovým zrcadlem a spojnou čočkou, Poloměr křivosti a ohnisková vzdálenost).

• Celkové řešení

  Zobrazovací rovnice pro tenkou čočku

  Změnu ohniskové vzdálenosti čočky \(f\) v závislosti na změně poloměrů křivosti optických ploch \(r_{1}\) a \(r_{2}\), popisuje zobrazovací rovnice. Budeme přepokládat, že se jedná o tenkou čočku: \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\left(\frac{1}{r_{1}}+\frac{1}{r_{2}}\right),\] kde \(n_{s}\) je index lomu skla a \(n_{v}\) je index lomu vzduchu.

   

  Vyjádření poloměru křivosti

  Poloměr křivosti \(r_{1}\) se blíží k nekonečnu. Z toho plyne, že zlomek \(\frac{1}{r_{1}}\) se blíží k nule. A proto nám tento člen ze zobrazovací rovnice „zmizí“:

  \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\frac{1}{r_{2}}.\]

  Poloměr křivosti \(r_{2}\) si označíme jako \(r\) (\(r_{2}=r\)):

  \[\frac{1}{f}=\left(\frac{n_{s}}{n_{v}}−1\right)\frac{1}{r}.\]

  Obě strany rovnice vynásobíme výrazem \(r\cdot f\): \[r=\left(\frac{n_{s}}{n_{v}}−1\right)f.\]

  Číselné řešení

  Ze zadání víme:

  \(n_{s}=1{,}5\) (index lomu skla)

  \(f=−10 \mathrm{cm}\) (ohnisková vzdálenost čočky)

  V tabulkách dohledáme hodnotu indexu lomu vzduchu :

  \(n_{v}=1{,}0\)

  Dosadíme:

  \(r=\left(\frac{n_{s}}{n_{v}}−1\right)f=\left(\frac{1{,}5}{1{,}0}−1\right)\cdot \left(−10\right) \mathrm{cm}=0{,}5\cdot \left(−10\right) \mathrm{cm}=−5 \mathrm{cm}.\)

  Jedná se o poloměr křivosti duté plochy, z toho důvodu nám jeho hodnota vyšla záporná.

• Odpověď

  Hodnota poloměru křivosti ploskoduté čočky je \(−5 \mathrm{cm}\).