Sbírka řešených úloh

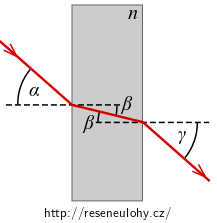
Průchod paprsku deskou

Úloha číslo: 1557

Skleněnou deskou tloušťky \(d\) s indexem lomu \(n\) prochází světelný paprsek, jak ukazuje následující obrázek.

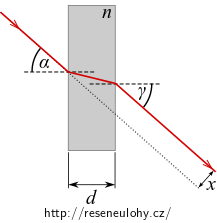
1) Ověřte, že vystupující paprsek je rovnoběžný s paprskem dopadajícím.

2) Ukažte, že posunutí paprsku je pro malé úhly \(\alpha \ll 1\) dáno vztahem

\[ x = d\,\frac{n-1}{n}\,\alpha. \]

• Teorie

  Při lomu paprsku na rozhraní dvou optických prostředí (označme je a a b) platí Snellův zákon lomu

  \[ \frac{\sin \alpha}{\sin \beta} = \frac{n_b}{n_a}, \]

  kde \(\alpha\) je úhel dopadu, \(\beta\) úhel lomu a \(n_a, n_b\) indexy lomu optických prostředí.

• 1) Nápověda – zachování směru paprsku

  Jaký vztah musí být mezi úhly \(\alpha\) a \(\gamma\), aby byl vystupující paprsek rovnoběžný s paprskem dopadajícím? Ukažte to ze zákonů lomu na rozhraních.

• 1) Řešení nápovědy – zachování směru paprsku

  Vystupující paprsek bude rovnoběžný s paprskem dopadajícím, jestliže bude platit rovnost \(\alpha=\gamma\).

  Zakresleme si do obrázku všechny úhly dopadu a lomu.

  

  Neboť je deska rovná, tj. její stěny jsou rovnoběžné, jsou rovnoběžné i naznačené kolmice. Vyznačené úhly \(\beta\) jsou shodné, neboť se jedná o úhly střídavé.

  Napíšeme zákony lomu pro obě rozhraní

  \[ \begin{eqnarray} \mathrm{1.\,rozhraní:}\qquad \frac{\sin{\alpha}}{\sin\beta} &=& \frac{n}{1} \qquad \Rightarrow \qquad \sin\alpha = n\sin\beta, \tag{1}\\ \mathrm{2.\,rozhraní:}\qquad \frac{\sin{\beta}}{\sin\gamma} &=& \frac{1}{n} \qquad \Rightarrow \qquad n\sin\beta = \sin\gamma. \tag{2} \end{eqnarray} \]

  Předpokládáme, že okolním prostředím je vakuum, případně vzduch, jehož index lomu je přibližně stejný jako vakuum \(n_\mathrm{vzduch} = 1{,}0003 \doteq 1 = n_\mathrm{vakuum}\).

  Porovnáním rovnic (1) a (2) získáme rovnost

  \[ \sin\alpha = \sin\gamma. \]

  Všechny úhly dopadu i lomu uvažujeme z intervalu \((0,\frac{\pi}{2}\rangle\). Funkce sinus je na tomto intervalu prostá, proto můžeme psát rovnost argumentů

  \[ \alpha = \gamma. \]

  Tím je rovnoběžnost vystupujícího a dopadajícího paprsku dokázána.

• 2) Nápověda – vztah pro posunutí

  Nalezněte v zadání představenou závislost \(x(d,\alpha)\) platnou pro \(\alpha \ll 1\).

  Úhly \(\alpha\) a \(\beta\) jsou vázány, jak jsme zjistili v předchozí části, vztahem

  \[ \frac{\sin\alpha}{\sin\beta} = n. \]

  Při úpravách se budou hodit přibližné vztahy pro \(\alpha \ll 1\)

  \[ \begin{eqnarray} \sin x &\doteq& x,\\ \cos x &\doteq& 1.\\ \end{eqnarray} \]

• 2) Řešení nápovědy – vztah pro posunutí

  Délku paprsku v desce označme \(a\).

  

  Našim cílem je určit \(x\). V pravoúhlém trojúhelníku s odvěsnou \(x\) platí

  \[ \sin (\alpha-\beta) = \frac{x}{a} \qquad \Rightarrow \qquad x = a\sin(\alpha-\beta). \tag{3}\]

  Délku \(a\) můžeme vyjádřit z dalšího pravoúhlého trojúhelníka

  \[ \cos \beta = \frac{d}{a} \qquad \Rightarrow \qquad a = \frac{d}{\cos\beta}. \tag{4}\]

  Vyloučením \(a\) z rovnic (3) a (4) dostáváme vztah

  \[ x = d\frac{\sin(\alpha-\beta)}{\cos\beta}. \]

  Je-li \(\alpha \ll 1\), pak i \(\beta \ll 1\), neboť při lomu ke kolmici je \(\beta \lt \alpha\).
  Tudíž je \(\alpha - \beta \ll 1\) a platí \(\sin(\alpha - \beta) \approx \alpha-\beta\). Současně je i \(\cos\beta \approx 1\). Dosazením dostáváme

  \[x = d\frac{\alpha-\beta}{1} \qquad\mathrm{pro\,}\alpha \ll 1.\tag{5}\]

  Pro \(\alpha,\beta \ll 1\) přejde vazba

  \[ \frac{\sin\alpha}{\sin\beta} = n\quad \mathrm{na} \quad \frac{\alpha}{\beta} = n. \tag{6}\]

  Dosazením \(\frac{\alpha}{n}\) za \(\beta\) v (5) z rovnice (6) máme

  \[x = d\left(\alpha - \frac{\alpha}{n}\right) =d\,\frac{n-1}{n}\,\alpha \qquad\mathrm{pro\,}\alpha \ll 1,\]

  což je hledaný vztah.

• CELKOVÉ ŘEŠENÍ

  K řešení použijeme výsledek úlohy Lom na soustavě rovnoběžných vrstev

  Z této úlohy vyplývá, že v našem případě platí

  \[ \sin\alpha = \sin\gamma. \] \[\alpha = \gamma\]

  Tímto jsme dokázali rovnoběžnost dopadjícího a vystupujícího paprsku.

  Chceme určit posunutí \(x\) vycházejícího paprsku.

  

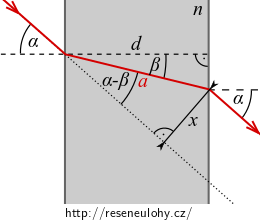
  Délku paprsku v desce označme \(a\).

  V pravoúhlém trojúhelníku s odvěsnou \(x\) platí

  \[ \sin (\alpha-\beta) = \frac{x}{a} \qquad \Rightarrow \qquad x = a\sin(\alpha-\beta). \]

  Délku \(a\) můžeme vyjádřit z dalšího pravoúhlého trojúhelníka

  \[ \cos \beta = \frac{d}{a} \qquad \Rightarrow \qquad a = \frac{d}{\cos\beta}. \]

  Vyloučením \(a\) z předchozích dvou rovnic dostáváme vztah

  \[ x = d\frac{\sin(\alpha-\beta)}{\cos\beta}. \]

  Je-li \(\alpha \ll 1\), pak i \(\beta \ll 1\), neboť při lomu ke kolmici je \(\beta \lt \alpha\).
  Tudíž je \(\alpha - \beta \ll 1\) a platí \(\sin(\alpha - \beta) \approx \alpha-\beta\). Současně je i \(\cos\beta \approx 1\). Dosazením dostáváme

  \[x = d\frac{\alpha-\beta}{1} \qquad\mathrm{pro\,}\alpha \ll 1.\]

  Pro \(\alpha,\beta \ll 1\) přejde vazba

  \[ \frac{\sin\alpha}{\sin\beta} = n\quad \mathrm{na} \quad \frac{\alpha}{\beta} = n. \]

  Dosazením \(\frac{\alpha}{n}\) za \(\beta\) máme

  \[x = d\left(\alpha - \frac{\alpha}{n}\right) =d\,\frac{n-1}{n}\,\alpha \qquad\mathrm{pro\,}\alpha \ll 1,\]

  což je hledaný vztah.

• Odpověď

  Jsou-li stěny desky rovnoběžné, pak je vystupující paprsek rovnoběžný se směrem dopadajícího paprsku.

  Pro malé úhly dopadu \(\alpha \ll 1\) platí pro posunutí paprsku přibližný vztah

  \[x =d\,\frac{n-1}{n}\,\alpha.\]