Difrakce na mřížce
Úloha číslo: 1503
Mřížka s mřížkovou konstantou \(b\) a \(n\) podélnými vrypy je osvětlena světlem o vlnové délce \(\lambda\). Ve vzdálenosti \(L\) od mřížky je rovnoběžně umístěno stínítko.
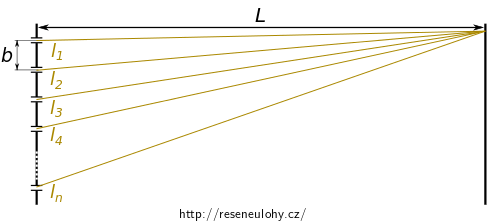
Stanovte průběh intenzity světla na stínítku za předpokladu, že štěrbiny sloužící jako koherentní zdroje světla jsou velmi úzké ve srovnání s jejich vzájemnou vzdáleností. Určete také vzdálenost hlavních maxim.
- Na štěrbiny dopadá kolmo rovinná harmonická vlna, lineárně polarizovaná ve směru štěrbin.
- Štěrbiny považujte za velmi úzké (aby první minimum ohybového jevu na jedné štěrbině bylo daleko mimo stínítko). Jinak řečeno předpokládejte, že při osvětlení jen jedné štěrbiny by díky ohybu na ní bylo osvětlení stínítka rovnoměrné.
- Řešte v aproximaci Fraunhoferova ohybu, \(L\gg nb\).
Úloha je rozšířením úlohy Youngův pokus, kde počítáme pouze se dvěma štěrbinami. Pro \(n=2\) by měl výsledek této úlohy dávat totéž.
Teorie
• Při výpočtu budeme používat komplexní formalismus, s nímž jsme se seznámili zde a pracovali jsme s ním v této úloze.
• Úlohu máme řešit v aproximaci tzv. Fraunhoferova ohybu, tj. interferenční obrazec budeme zkoumat na velmi vzdáleném stínítku. Právě díky této podmínce lze při výpočtu přistoupit k řadě zjednodušení.
• Štěrbiny jsou velmi úzké, budeme tedy předpokládat, že při osvětlení jen jedné štěrbiny by díky ohybu na ní bylo osvětlení stínítka rovnoměrné. Na štěrbiny proto budeme nahlížet jako na přímkové zdroje válcových vln. Elektrická intenzita vlny v místě vzdáleném \(\rho\) od zvolené štěrbiny je tedy
\[E_\mathrm{valc}(t,\rho) = \frac{\mathcal{E}_0}{\sqrt{r}} e^{i(\omega t - k\rho )},\]kde \(\mathcal{E}_0\) je veličina, jejíž velikost souvisí s intenzitou na štěrbiny dopadající rovinné vlny a šířkou štěrbiny.
• Intenzitu světla ve velké vzdálenosti, kde lze lokálně části válcových vln považovat za rovinné, vypočítáme pomocí vztahu
\[ I = \frac{1}{2z_0} EE^\star, \]kde hvězdička značí komplexní sdružení a \(z_0 = \sqrt{\frac{\mu_0}{\varepsilon_0}}\) je impedance vakua.
• Pro malé úhly \(\delta \ll 1\) je
\[ \sin\delta \,\approx\, \tan \delta . \]Nápověda 1 – superpozice elektrických intenzit
Nakreslete si obrázek situace v těsné blízkosti mřížky a naznačte dráhové rozdíly jednotlivých paprsků. Určete velikost elektrické intenzity vlny vzniklé součtem vln s průvodiči \(l_1,l_2\) až \(l_n\).
Poté si připravte komplexně sdruženou výslednou elektrickou intenzitu \(E^\star\).
Nápověda 2 – průběh intenzity na stínítku
Vypočítejte závislost intenzity světla na úhu \(\alpha\) podle vztahu
\[ I = \frac{1}{2z_0} EE^\star, \]dosazením právě vypočítané elektrické intenzity a jejího komplexního sdružení.
Nápověda 3 – vzdálenost hlavních maxim
Pro malé úhly \(\alpha\) určete šířku proužku interferenčního obrazce.
Jak závisí šířka obrazce na \(L,\lambda\) a \(b\)?
CELKOVÉ ŘEŠENÍ
Neboť stínítko bude od mřížky dostatečně daleko, budeme faktory \(\sqrt{l_i}\) úbytku amplitudy elektrické intenzity aproximovat konstantní hodnotou \(\sqrt{L}\).
Velikost elektrické intenzity vlny z první, druhé resp. \(n\)-té štěrbiny v daném místě stínítka, vzdáleném \(l_1,l_2\) resp. \(l_n\) od těchto štěrbin je
\[ \begin{eqnarray} E_1 &=& \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)},\\ E_2 &=& \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_2)},\\ &\vdots& \\ E_n &=& \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_n)}. \end{eqnarray} \]Výsledná intenzita v daném místě na stínítku je přímo součtem velikostí těchto intenzit, neboť kmitají stejným směrem. Postupnými úpravami dostaneme
\[ E = E_1 + E_2 + \ldots + E_n = \frac{\mathcal{E}_0}{\sqrt{L}} \left( e^{i(\omega t - kl_1)} + e^{i(\omega t - kl_2)} + \ldots + e^{i(\omega t - kl_n)} \right) = \] \[ =\frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \big(e^{-ik(\overbrace{l_1-l_1}^{\mathrm{ozn.\,}\Delta l_1})} + e^{-ik(\overbrace{l_2-l_1}^{\mathrm{ozn.\,}\Delta l_2})} + \ldots + e^{-ik(\overbrace{l_n-l_1}^{\mathrm{ozn.\,}\Delta l_n})} \big)= \] \[ = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \big(e^{-ik \Delta l_1} + e^{-ik \Delta l_2} + \ldots + e^{-ik \Delta l_n} \big)= \] \[ = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \sum_{j=1}^{n} e^{-ik \Delta l_j}. \tag{1}\]Budeme muset určit výsledek sčítání. Dráhový rozdíl \(j\)-tého paprsku oproti prvnímu paprsku vyjádříme pomocí násobku mřížkového parametru \(b\) a úhlu \(\alpha\).
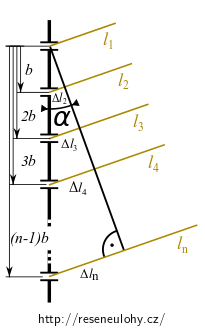
Je-li stínítko dostatečně daleko, můžeme paprsky ze štěrbin vycházející považovat za rovnoběžné a naznačený trojúhelník za pravoúhlý.
Proto platí
\[ \sin \alpha = \frac{\Delta l_j}{(j-1)b}. \] A odtud \(j\)-tý dráhový rozdíl \[ \Delta l_j = (j-1)b\sin\alpha. \]Dosazením tohoto vyjádření za \(\Delta l_j\) ve vztahu (1) dostaneme
\[ E = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \sum_{j=1}^{n} e^{-ik (j-1)b\sin\alpha}= \]Nyní vidíme, že suma představuje součet \(n\) členů geometrické posloupnosti s prvním členem \(1\) a kvocientem \(e^{-ikb\sin\alpha}\). Provedeme součet
\[ = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \sum_{j=1}^{n} \big(\underbrace{e^{-ik b\sin\alpha}}_{\mathrm{kvocient}}\big)^{j-1} = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \frac{\left(e^{-ikb\sin\alpha}\right)^n - 1 }{e^{-ikb\sin\alpha} - 1}. \]Po jednoduché úpravě máme velikost výsledné elektrické intenzity
\[ E = \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \frac{e^{-inkb\sin\alpha} - 1 }{e^{-ikb\sin\alpha} - 1}. \]Komplexně sdružená velikost výsledné elektrické intenzity je tak
\[ E^\star = \frac{\mathcal{E}_0}{\sqrt{L}} e^{-i(\omega t - kl_1)} \frac{e^{inkb\sin\alpha} - 1 }{e^{ikb\sin\alpha} - 1}. \]Vypočítané elektrické intenzity dosadíme do vztahu pro intenzitu světla
\[ I = \frac{1}{2z_0}EE^\star = \frac{\mathcal{E}_0^2}{2z_0 L} \underbrace{e^{i(\omega t - kl_1)}e^{-i(\omega t - kl_1)}}_{1} \frac{\big(e^{-inkb\sin\alpha} - 1\big)\big(e^{inkb\sin\alpha} - 1\big)}{\big(e^{-ikb\sin\alpha} - 1\big)\big(e^{ikb\sin\alpha} - 1\big)}. \]V čitateli i jmenovateli máme podobné výrazy.
Upravme nejprve zobecněný výraz
\[ \color{MidnightBlue}{ (e^{-i\xi} - 1)(e^{i\xi} - 1) = \underbrace{e^{-i\xi}e^{i\xi}}_{1} - e^{-i\xi} - e^{i\xi} + 1= 2 -(e^{-i\xi} + e^{i\xi})=} \] \[ \color{MidnightBlue}{=2-(\cos \xi - i \sin \xi + \cos \xi + i \sin \xi) = 4\frac{1-\cos \xi}{2} = 4 \sin^2 \frac{\xi}{2}.} \]Užitím zobecněného vyjádření v čitateli i jmenovateli pak máme
\[ I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\big(e^{-inkb\sin\alpha} - 1\big)\big(e^{inkb\sin\alpha} - 1\big)}{\big(e^{-ikb\sin\alpha} - 1\big)\big(e^{ikb\sin\alpha} - 1\big)} = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}}. \]Vykreslíme graf této závislosti \(I=I(\sin\alpha)\)
\[ I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}}. \tag{2}\]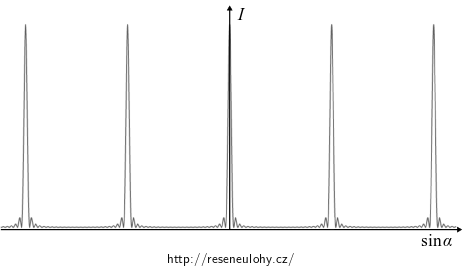
Na stínítku bychom pozorovali sérii ostrých maxim.
Pro malé úhly \(\alpha \ll 1\) je
\[\sin\alpha \,\approx\,\tan \alpha = \frac{x}{L},\]kde úhel \(\alpha\) je odchylka směru paprsků od normály stínítka.
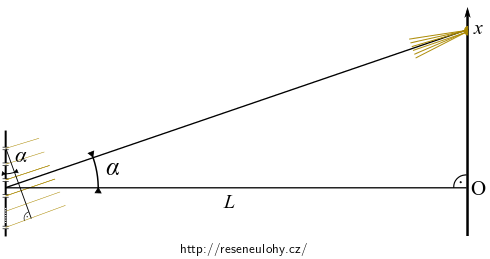
Dosazením \(\frac{x}{L}\) za \(\sin \alpha\) ve vztahu (2) máme
\[ I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkbx}{2L}}{\sin^2 \frac{kbx}{2L}}. \tag{3}\]Určíme vzdálenost sousedních hlavních maxim interferenčního obrazce.
Funkce ve jmenovateli průběhu (3) je modulována „rychlou“ funkcí v čitateli, která vytváří velké množství vedlejších maxim.
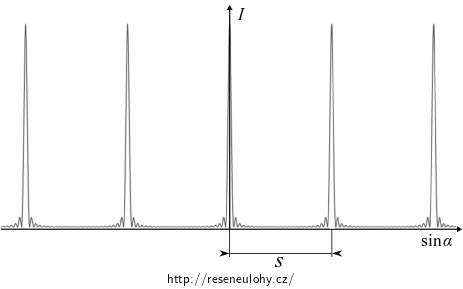
První hlavní maximum intenzity nastane, jestliže funkce ve jmenovateli jde poprvé limitně k nule, tj. pro takovou souřadnici \(x=s\), kdy
\[ \frac{kbs}{2L} = \pi \qquad \Rightarrow \qquad s=\frac{2L\pi}{kb}=\frac{\lambda L}{ b}, \]kde jsme použili vztah \(k=\frac{2\pi}{\lambda}\).
Vzdálenost sousedních hlavních maxim je tedy
\[ s=\frac{\lambda L}{b}. \]Se zvětšující se vzdáleností \(L\) stínítka od mřížky a s rostoucí vlnovou délkou \(\lambda\) se bude interferenční obrazec rozšiřovat, se zvětšováním mřížkového parametru \(b\) se bude naopak zhušťovat.
Odpověď
Při aproximaci na vzdálené stínítko jsme dostali následující průběh intenzity
\[ I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}}, \]kde \(\alpha\) je úhel, který svírá normála stínítka se směrem interferujících paprsků.
Graf \(I=I(\sin\alpha)\).

Námi vypočítaný průběh intenzity, jak jej vidíme na grafu, bude dobře popisovat oblast v blízkosti středu stínítka. Ve vzdálenějších oblastech od středu se již bude projevovat pokles intenzit hlavních maxim, související s ohybem na jednotlivých štěrbinách.
Určili jsme souvislost vzdálenosti hlavních maxim a ostatních parametrů
\[ s \,\approx\, \frac{\lambda L}{b}. \]Se zvětšující se vzdáleností \(L\) stínítka od mřížky a s rostoucí vlnovou délkou \(\lambda\) se bude interferenční obrazec rozšiřovat, se zvětšováním mřížkového parametru \(b\) se bude naopak zhušťovat.
Komentář – konečnost intenzity v maximech
Možná se zdá zvláštní, že obrazec intenzity určený funkcí
\[ I = \frac{\mathcal{E}_0^2}{2z_0 L} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}}. \]je všude konečný.

Výraz ve jmenovateli jde přeci pro \(\sin\alpha \to 0\) také k nule, takže maximum \(I\) by zde mělo jít k nekonečnu. Kde je chyba?
Nelze zkoumat chování jmenovatele bez přihlédnutí k funkci v čitateli. Musíme hledat limitní hodnotu zlomku jako celku. Matematicky
\[\small \lim_{\xi \to 0} {\frac{\sin^2{n\xi}}{\sin^2 \xi}} = \lim_{\xi \to 0} \left({\frac{\sin {n\xi}}{n\xi}} \frac{n\xi}{\sin \xi}\right)^2 = n^2 \left(\underbrace{\lim_{\xi \to 0}\frac{\sin {n\xi}}{n\xi}}_{1} \cdot \underbrace{\lim_{\xi \to 0}\frac{\xi}{\sin {\xi}}}_{1}\right)^2 = n^2. \]V našem konkrétním případě
\[ I_0 = \lim_{\sin\alpha\to 0} I = \frac{\mathcal{E}_0^2}{2z_0 L} \lim_{\sin\alpha\to 0} \frac{\sin^2 \frac{nkb\sin\alpha}{2}}{\sin^2 \frac{kb\sin\alpha}{2}} = \frac{\mathcal{E}_0^2}{2z_0 L}n^2 \]Intenzita v maximech je opravdu konečná. Roste se zvětšující se amplitudou dopadající vlny a s počtem osvětlených štěrbin, naopak klesá s rostoucí vzdáleností stínítka.


