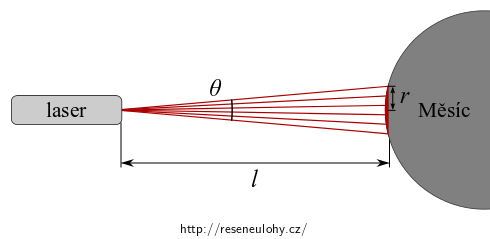
Divergence laserového svazku
Úloha číslo: 1553
Helium-neonový laser vyzařující na vlnové délce \(632{,}8~\mathrm{nm}\) vysílá záření, které se šíří ve tvaru kruhového kužele. Divergence svazku tohoto laseru je \(\theta = 1{,}4~\mathrm{mrad}\). Namíříme-li laser na Měsíc, budeme na jeho povrchu pozorovat ozářený kruh. Určete jeho obsah.
Rozbor
Divergence svazku udává velikost vrcholového úhlu kužele, ve kterém se záření vyslané laserem šíří.

Tato divergence není záměrná, při konstrukci laseru je obvykle snaha hodnotu \(\theta\) minimalizovat. Pro přesná měření, kde je požadován svazek konstantní tloušťky, je nutno sbíhavost či rozbíhavost svazku korigovat zařazením speciálních optických prvků (soustava čoček) na výstupu laseru.
Velikost laserem ozářené plochy Měsíce je úměrná vzdálenosti laser-Měsíc. Vzdálenost Země-Měsíc nalezneme v tabulkách.
Nápověda 1 – nakreslení situace
Nakreslete situaci, kdy na Zemi je umístěn laser, který vysílá světelné paprsky ve formě úzkého kuželu a osvětluje část Měsíce. Vyznačte úhel \(\theta\), vzdálenost od Měsíce \(l\) a poloměr hranice ozářené oblasti \(r\).
Nápověda 2 – výpočet
V tabulkách vyhledejte vzdálenost \(l\) Měsíce od Země. Ze vzdálenosti \(l\) a znalosti úhlu \(\theta\) určete poloměr \(r\) a následně obsah ozářené plochy.
CELKOVÉ ŘEŠENÍ
Nejdříve si nakreslíme situaci, kdy na Zemi je umístěn laser, který vysílá světelné paprsky ve formě úzkého kuželu a osvětluje část Měsíce.
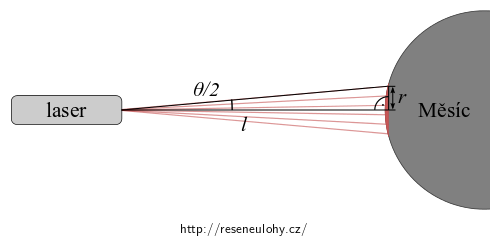
Za vzdálenost \(l\) považujeme vzdálenost Měsíce od Země, kterou nalezneme v tabulkách:
\[ l = 384\,400~\mathrm{km}. \]V naznačeném pravoúhlém trojúhelníku platí
\[ \mathrm{tg}\, \frac{\theta}{2} = \frac{r}{l}. \]Odtud snadno vyjádříme poloměr
\[ r = l \,\mathrm{tg}\, \frac{\theta}{2}. \]Kolmý průmět osvětleného kulového vrchlíku budeme kruh o obsahu
\[ S = \pi r^2 = \pi l^2 \mathrm{tg}\,^2 \frac{\theta}{2}= \pi\, 384400^2 \mathrm{tg}\,^2 \frac{1{,}4{\cdot} 10^{-3}}{2}~\mathrm{km^2} \doteq 227{\cdot} 10^{3}~\mathrm{km^2}. \]Diskuze - poměr poloměrů osvětleného kruhu a Měsíce
Porovnejme vypočítaný obsah osvětleného průmětu s průřezem celého měsíce. Rovníkový průměr Měsíce je \(D_\mathrm{M} = 3476~\mathrm{km}\), obsah jeho průřezu je tedy
\[ S_\mathrm{M} = \frac{\pi D_\mathrm{M}^2}{4} = \frac{\pi\,3476^2}{4}\, \mathrm{km}^2~\doteq~ 9{,}5{\cdot} 10^6~\mathrm{km^2}. \]Poměr laserem osvětlené části a obsahu celého průřezu Měsíce je
\[ \frac{S}{S_\mathrm{M}} = \frac{227{\cdot} 10^{3}}{9{,}5{\cdot} 10^6} ~\doteq~ 24{\cdot} 10^{-3}. \]Poloměry obou kruhů budou v poměru \(\sqrt{24{\cdot} 10^{-3}}\).
Pro názornost obrázek v měřítku:

Poloměry kruhů jsou voleny tak, aby byl splněn právě vypočítaný poměr.
Odpověď
Pozorujeme kruhový průmět osvětleného kulového vrchlíku o obsahu \(227{\cdot} 10^{3}~\mathrm{km^2}\).
Na první pohled malé číslo divergence \(\theta\) způsobí na velké vzdálenosti Země-Měsíc obrovské rozšíření svazku. Vzhledem k rozměrům Měsíce však tvoří osvětlená část stále „pouze“ asi \(\frac{1}{167}\) obsahu jeho průřezu.