Difrakce na kruhovém otvoru
Úloha číslo: 1670
Kruhová spojná čočka o průměru 32 mm a s ohniskovou vzdáleností 24 cm vytváří ve své ohniskové rovině obrazy vzdálených bodových objektů. Používá se světlo o vlnové délce 550 nm.
a) Bereme v úvahu difrakci na aparatuře čočky. Jakou úhlovou vzdálenost musejí mít dva bodové objekty, aby splňovaly Rayleighovo kritérium rozlišení?
b) Jaká je vzdálenost Δx středů obrazů v ohniskové rovině?
Obrázek situace
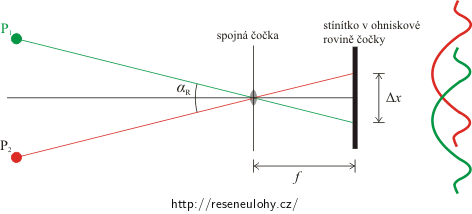
Na obrázku jsme si označili: P1 a P2 jsou bodové zdroje, f je ohnisková vzdálenost čočky, Δx je vzdálenost difrakčních obrazů na stínítku, αR je rozlišovací úhlová vzdálenost bodových zdrojů.
Křivky vpravo znázorňují intenzitu světla na stínítku od jednotlivých zdrojů.
Nápověda 1
Tato úloha se zabývá difrakcí na kruhovém otvoru, jaký tvoří například kruhová čočka, jíž prochází světlo. Jestliže máme bodový zdroj, potom jeho difrakčním obrazcem je kruhový disk obklopený několika sekundárními kroužky, jejichž intenzita postupně slábne, viz obrázek (obrázek je převzat z http://www.goldastro.com/goldfocus/resolving_power.php). Analýza takových obrazců je složitá.

Platí ovšem, že první minimum difrakčního obrazce (první tmavý kroužek) na kruhovém otvoru o průměru d nastává, když
\[\sin \alpha=\, 1{,}22\,\frac{\lambda}{d},\]kde úhel α je úhel mezi osou kruhového otvoru a směrem k některému z bodů prvního (kruhového) minima.
Jestliže chceme rozlišit difrakční obrazce dvou bodových zdrojů, potřebujeme, aby jejich úhlová vzdálenost byla taková, že centrální maximum difrakčního obrazce jednoho zdroje je alespoň v místě prvního minima difrakčního obrazce druhého zdroje. Této podmínce se říká Rayleighovo kritérium rozlišení.
Jaká tuto podmínku vyjádřit matematicky?
Nápověda 2
Jak můžeme vypočítat vzdálenost středů difrakčních obrazů pomocí ohniskové vzdálenosti? Využijte obrázek výše.
Zápis
d = 32 mm = 32·10−3 m průměr čočky λ = 550 nm = 5,5·10−7 m vlnová délka použitého světla f = 24 cm = 0,24 m ohnisková vzdálenost čočky αR = ? (rad) úhlová vzdálenost dvou bodových objektů Δx = ? (µm) vzdálenost středů obrazů Řešení

Na obrázku jsme si označili: P1 a P2 jsou bodové zdroje, f je ohnisková vzdálenost čočky, Δx je vzdálenost difrakčních obrazů na stínítku, αR je rozlišovací úhlová vzdálenost bodových zdrojů.
Při difrakci na kruhovém otvoru, například kruhové čočce platí, že první minimum difrakčního obrazce na kruhovém otvoru o průměru d nastává, když
\[\sin \alpha=\, 1{,}22\,\frac{\lambda}{d},\]kde úhel α je úhel mezi osou kruhového otvoru a směrem k některému z bodů prvního (kruhového) minima.
Pokud chceme rozlišit difrakční obrazce dvou bodových zdrojů, potřebujeme, aby jejich úhlová vzdálenost byla taková, že centrální maximum difrakčního obrazce jednoho zdroje je v místě prvního minima difrakčního obrazce druhého zdroje. Takové podmínce říkáme Rayleighovo kritérium. Dva bodové zdroje musejí mít úhlovou vzdálenost:
\[\alpha_\mathrm{R}=\,\arcsin\,\frac{1{,}22\lambda}{d}\]Poněvadž jde o malé úhly, můžeme nahradit sin αR úhlem αR vyjádřeným v radiánech. Získáme:
\[\alpha_\mathrm{R}=\,1{,}22\cdot\frac{\lambda}{d}.\]Do výsledného vztahu dosadíme číselně:
\[\alpha_\mathrm{R}=\,1{,}22\cdot\frac{\lambda}{d}=\,1{,}22\cdot\frac{5{,}5{\cdot}10^{−7}}{32{\cdot}10^{−3}}\,\dot=\,2{,}1{\cdot}10^{−5}\, \mathrm{rad}.\]Na obrázku využijeme trojúhelníku mezi čočkou a stínítkem a dostaneme vztah:
\[\mathrm{tg}\,\,\frac{\alpha_\mathrm{R}}{2}=\,\frac{\mathrm{Δ}x}{2f}.\]Vyjádříme Δx a využijeme, že jde o malé úhly, a tedy můžeme tg αR nahradit úhlem αR v radiánech.
\[\mathrm{Δ}x=\,f\alpha_\mathrm{R}.\]Dosadíme číselné hodnoty.
\[\mathrm{Δ}x=\,f\alpha_\mathrm{R}=\,1{,}22f\frac{\lambda}{d}=\,1{,}22\,\cdot\,0{,}24\cdot\frac{5{,}5{\cdot}10^{−7}}{32{\cdot}10^{−3}}\,\mathrm{m}\,\dot=\,\,5{\cdot}10^{−6}\,\mathrm{m}=\, 5\,\mathrm{\mu m}.\]Odpověď
Dva bodové objekty musí mít úhlovou vzdálenost 2,1·10−5 rad a vzdálenost středů obrazů je 5 µm.

