Sbírka řešených úloh

Lom na soustavě rovnoběžných vrstev

Úloha číslo: 1554

Uvažujme následující soustavu optických prostředí tvořenou systémem \(m+1\) rovinných vrstev s indexy lomu \(n_1,n_2,\ldots,n_{m+1}\).

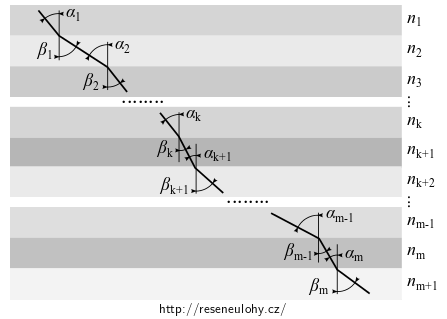
Nechť na první rozhraní dopadá paprsek pod takovým úhlem \(\alpha_1\), že na žádném rozhraní nedochází k totálnímu odrazu.

Určete směr paprsku \(\beta_m\) vystupujícího z \(m\)-tého rozhraní.

• Teorie

  Při lomu paprsku na rozhraní dvou optických prostředí (a a b) platí Snellův zákon lomu

  \[ \frac{\sin \alpha}{\sin \beta} = \frac{n_b}{n_a}, \]

  kde \(\alpha\) je úhel dopadu, \(\beta\) úhel lomu a \(n_a, n_b\) po řadě indexy lomu těchto prostředí.

• Nápověda 1 – zákony lomu na jednotlivých rozhraních

  Napište zákony lomu pro první až \(m\)-té rozhraní.

• Řešení nápovědy 1 – zákony lomu na jednotlivých rozhraních

  Napíšeme zákony lomu pro každé z rozhraní.

  

  Pro každé rozhraní platí, že poměr sinů úhlu dopadu a lomu je roven opačnému poměru indexu lomu obou prostředí.

  Tedy

  \[ \begin{eqnarray} \frac{\sin\alpha_1}{\sin\beta_1} &=& \frac{n_2}{n_1},\\ \frac{\sin\alpha_2}{\sin\beta_2} &=& \frac{n_3}{n_2},\\ \vdots &\phantom{=}& \vdots\\ \frac{\sin\alpha_k}{\sin\beta_k} &=& \frac{n_{k+1}}{n_k},\\ \frac{\sin\alpha_{k+1}}{\sin\beta_{k+1}} &=& \frac{n_{k+2}}{n_{k+1}},\\ \vdots &\phantom{=}& \vdots\\ \frac{\sin\alpha_{m-1}}{\sin\beta_{m-1}} &=& \frac{n_m}{n_{m-1}},\\ \frac{\sin\alpha_m}{\sin\beta_m} &=& \frac{n_{m+1}}{n_m}.\\ \end{eqnarray} \]

  Přitom předpokládáme, že úhel \(\alpha_1\) vstupujícího paprsku, je takový, že nedochází k totálnímu odrazu na žádném z rozhraní.

• Nápověda 2 – uvážení geometrie systému

  Na základě geometrie systému rozvažte, jak spolu souvisí úhly

  \[ \beta_1~\mathrm{a}~\alpha_2,\quad \beta_2~\mathrm{a}~\alpha_3,\quad\ldots\quad \beta_i~\mathrm{a}~\alpha_{i+1},\quad\ldots\quad \beta_{m-1}~\mathrm{a}~\alpha_m. \]

  

• Řešení nápovědy 2 – uvážení geometrie systému

  Neboť jsou rozhraní rovnoběžná, jsou zmíněné úhly souhlasné a platí rovnost

  \[ \beta_i = \alpha_{i+1}, \qquad i = 1,\ldots,m-1. \]

• Nápověda 3 – řešení soustavy rovnic

  Rovnost souhlasných úhlů využijte při řešení soustavy zákonů lomu. Cílem řešení soustavy je určit směr vystupujícího paprsku \(\beta_m\).

• Řešení nápovědy 3 – řešení soustavy rovnic

  Z rovnosti souhlasných úhlů vyplývá, že výrazy stejné barvy

  \[ \begin{eqnarray} \frac{\sin\alpha_1}{\color{blue}{\sin\beta_1}} &=& \frac{n_2}{n_1},\\ \frac{\color{blue}{\sin\alpha_2}}{\sin\beta_2} &=& \frac{n_3}{n_2},\\ \vdots &\phantom{=}& \vdots\\ \frac{\sin\alpha_k}{\color{magenta}{\sin\beta_k}} &=& \frac{n_{k+1}}{n_k},\\ \frac{\color{magenta}{\sin\alpha_{k+1}}}{\sin\beta_{k+1}} &=& \frac{n_{k+2}}{n_{k+1}},\\ \vdots &\phantom{=}& \vdots\\ \frac{\sin\alpha_{m-1}}{\color{green}{\sin\beta_{m-1}}} &=& \frac{n_m}{n_{m-1}},\\ \frac{\color{green}{\sin\alpha_m}}{\sin\beta_m} &=& \frac{n_{m+1}}{n_m},\\ \end{eqnarray} \]

  se v této soustavě rovnic rovnají.

  Před řešením této soustavy všechny rovnice „křížově“ pronásobíme

  \[ \begin{eqnarray} n_1 \sin\alpha_1 &=& n_2 \color{blue}{\sin\beta_1},\\ n_2 \color{blue}{\sin\alpha_2} &=& n_3 \sin\beta_2,\\ \vdots &\phantom{=}& \vdots\\ n_k \sin\alpha_k &=& n_{k+1} \color{magenta}{\sin\beta_k},\\ n_{k+1} \color{magenta}{\sin\alpha_{k+1}} &=& n_{k+2} \sin\beta_{k+1},\\ \vdots &\phantom{=}& \vdots\\ n_{m-1} \sin\alpha_{m-1} &=& n_m \color{green}{\sin\beta_{m-1}},\\ n_m \color{green}{\sin\alpha_m} &=& n_{m+1} \sin\beta_m. \end{eqnarray} \]

  Díky rovnosti stejnobarevných výrazů se rovná vždy pravá strana rovnice s levou stranou rovnice následující. Proto se rovná i první a poslední člen

  \[ n_1 \sin\alpha_1 = n_{m+1} \sin\beta_m. \] Tedy \[ \sin\beta_m = \frac{n_1}{n_{m+1}}\sin\alpha_1. \]

  Úhel \(\beta_m\) vystupujícího paprsku závisí pouze na počátečním úhlu dopadu \(\alpha_1\) a na indexech lomu prvního a posledního prostředí.

• CELKOVÉ ŘEŠENÍ

  Při lomu paprsku na rozhraní dvou optických prostředí (a a b) platí Snellův zákon lomu

  \[ \frac{\sin \alpha}{\sin \beta} = \frac{n_b}{n_a}, \]

  kde \(\alpha\) je úhel dopadu, \(\beta\) úhel lomu a \(n_a, n_b\) po řadě indexy lomu těchto prostředí.

  Rozepíšeme si zákony lomu pro všechna rozhraní.

  

  Tím dostáváme soustavu m rovnic.

  \[ \begin{eqnarray} \frac{\sin\alpha_1}{\sin\beta_1} &=& \frac{n_2}{n_1},\\ \frac{\sin\alpha_2}{\sin\beta_2} &=& \frac{n_3}{n_2},\\ \vdots &\phantom{=}& \vdots\\ \frac{\sin\alpha_{m-1}}{\sin\beta_{m-1}} &=& \frac{n_m}{n_{m-1}},\\ \frac{\sin\alpha_m}{\sin\beta_m} &=& \frac{n_{m+1}}{n_m}.\\ \end{eqnarray} \]

  Vzhledem k rovnoběžnosti rozhraní plátí následující rovnost

  \[ \beta_i = \alpha_{i+1}, \qquad i = 1,\ldots,m-1. \]

  Tuto rovnost použijeme při řešení soustavy rovnic. Výrazy stejné barvy se v této soustavě rovnic rovnají.

  \[ \begin{eqnarray} \frac{\sin\alpha_1}{\color{blue}{\sin\beta_1}} &=& \frac{n_2}{n_1},\\ \frac{\color{blue}{\sin\alpha_2}}{\sin\beta_2} &=& \frac{n_3}{n_2},\\ \vdots &\phantom{=}& \vdots\\ \frac{\sin\alpha_{m-1}}{\color{green}{\sin\beta_{m-1}}} &=& \frac{n_m}{n_{m-1}},\\ \frac{\color{green}{\sin\alpha_m}}{\sin\beta_m} &=& \frac{n_{m+1}}{n_m},\\ \end{eqnarray} \]

  Po pronásobení rovnic dostáváme

  \[ \begin{eqnarray} n_1 \sin\alpha_1 &=& n_2 \color{blue}{\sin\beta_1},\\ n_2 \color{blue}{\sin\alpha_2} &=& n_3 \sin\beta_2,\\ \vdots &\phantom{=}& \vdots\\ n_{m-1} \sin\alpha_{m-1} &=& n_m \color{green}{\sin\beta_{m-1}},\\ n_m \color{green}{\sin\alpha_m} &=& n_{m+1} \sin\beta_m. \end{eqnarray} \]

  Ze soustavy rovnic vidíme, že pravá strana rovnice se vždy rovná levé straně následující rovnice. Z tohoto pozorování získáváme jednu rovnici pro celou soustavu.

  \[ n_1 \sin\alpha_1 = n_{m+1} \sin\beta_m. \]

  Řešením této rovnice získáváme

  \[ \sin\beta_m = \frac{n_1}{n_{m+1}}\sin\alpha_1. \]

  Vidíme, že úhel \(\beta_m\) závisí pouze na počátečním úhlu dopadu \(\alpha_1\) a na indexech lomu prvního a posledního prostředí.

• Odpověď

  Úhel \(\beta_m\) vystupujícího paprsku závisí pouze na počátečním úhlu dopadu \(\alpha_1\) a na indexech lomu prvního a posledního prostředí, a to vztahem

  \[ \sin\beta_m = \frac{n_1}{n_{m+1}}\sin\alpha_1. \]

  Na indexech lomu vnitřních prostředí nezáleží!