Index lomu hranolu

Úloha číslo: 1558

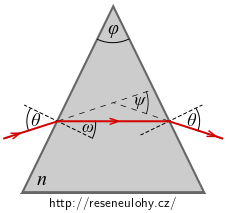
K určení indexu lomu \(n\) skla trojbokého hranolu jsme provedli měření, jak naznačuje obrázek vpravo.

Úzký svazek světla jsme nechali dopadat na první rozhraní pod takovým úhlem \(\theta\), aby pod stejným úhlem \(\theta\) vystupoval z rozhraní druhého.

Zjistili jsme, že deviační úhel, což je celkový úhel, o který se paprsek při průchodu hranolem odchýlí, je \(\psi\).

Nalezněte vztah, podle kterého lze z naměřených hodnot \(\varphi,\psi\) určit neznámý index lomu \(n\) hranolu.

Teorie
Při lomu paprsku na rozhraní dvou optických prostředí (a a b) platí Snellův zákon lomu
\[ \frac{\sin \alpha}{\sin \beta} = \frac{n_b}{n_a}, \]
kde \(\alpha\) je úhel dopadu, \(\beta\) úhel lomu a \(n_a, n_b\) indexy lomu optických prostředí.
Nápověda 1 – zákon lomu
Cílem úlohy je určit závislost indexu lomu \(n\) na úhlech \(\varphi\) a \(\psi\). Souvislost mezi indexem lomu a úhly lze získat ze zákona lomu na rozhraní. Napište jej.
Řešení nápovědy 1 – zákon lomu
Ze symetrie problému je lhostejné, které rozhraní si vybereme.

Pro první rozhraní, kterým paprsek prochází, platí
\[ \frac{\sin\theta}{\sin\omega} = \frac{n}{1} \tag{1}\]
kde jsme úhel lomu označili \(\omega\) a index lomu okolního prostředí uvážili \(1\).
Nápověda 2 – vyjádření ω
Rovnice (1) dává závislost hledaného indexu lomu na úhlech \(\theta, \omega\). Našim cílem je ale najít závislost na měřených hodnotách \(\varphi, \psi\).

Vyjádřete úhel \(\omega\) pomocí naměřených úhlů \(\varphi, \psi\).
Řešení nápovědy 2 – vyjádření ω
Vyjádříme úhel \(\omega\) pomocí naměřených úhlů.

Velikost vrcholového úhlu \(\varphi\) hranolu má i vnější úhel při vrcholu B.

Vezmeme čtyřúhelník ABCD, u kterého víme, že součet vnitřních úhlů musí být 360°. Úhly u vrcholů A i C jsou pravé. Úhel u vrcholu B je \(180° - \varphi\). Díky tomu je vedlejší úhel u vrcholu B roven \(\varphi\).

Pro rovnoramenný \(\Delta ABC\) platí
\[ \varphi = \omega + \omega, \]
a odtud snadno
\[ \omega = \frac{\varphi}{2}. \tag{2}\]
Nápověda 3 – vyjádření θ
Rovnice (1) dává závislost hledaného indexu lomu na úhlech \(\theta, \omega\). Našim cílem je ale najít závislost na měřených hodnotách \(\varphi, \psi\).

Vyjádřete úhel \(\theta\) pomocí naměřených úhlů \(\varphi, \psi\).
Řešení nápovědy 3 – vyjádření θ
Vyjádříme úhel \(\theta\) pomocí naměřených úhlů.

Pro úhly \(\theta, \nu, \omega\) s vrcholem v bodě \(\mathrm{A}\) platí
\[ \theta = \nu + \omega. \tag{3}\]
Úhel \(\omega\) máme vyjádřený pomocí \(\varphi\) vztahem (2), zbývá vyjádřit \(\nu\) pomocí \(\psi\).

Vnější úhel \(\psi\) při vrcholu \(D\) v \(\Delta ACD\) je roven součtu vnitřních úhlů u zbývajících vrcholů. Neboť je trojúhelník rovnoramenný, platí
\[ \psi = \nu + \nu. \]
Odtud snadno
\[\nu = \frac{\psi}{2}.\tag{4}\]
Dosazením (2) a (4) do (3) máme
\[ \theta = \nu + \omega = \frac{\psi+\varphi}{2}. \tag{5}\]
Nápověda 4 – výsledný vztah
Dosaďte nalezená vyjádření (2) a (5) do zákona lomu (1).
Řešení nápovědy 4 – výsledný vztah
V předchozích částech jsme našli následující vyjádření úhlů \(\omega\) a \(\theta\)
\[ \omega = \frac{\varphi}{2}, \] \[ \theta = \frac{\psi + \varphi}{2}. \]
Dosazením do zákona lomu
\[ n=\frac{\sin\theta}{\sin\omega}, \]
dostáváme hledaný vztah
\[ n=\frac{\sin \frac{\psi + \varphi}{2} }{\sin\frac{\varphi}{2}}. \]
CELKOVÉ ŘEŠENÍ
Při lomu paprsku na rozhraní dvou optických prostředí platí Snellův zákon lomu
\[ \frac{\sin \alpha}{\sin \beta} = \frac{n_b}{n_a}, \]
kde \(\alpha\) je úhel dopadu, \(\beta\) úhel lomu a \(n_a, n_b\) indexy lomu optických prostředí.

V našem případě platí
\[ \frac{\sin\theta}{\sin\omega} = \frac{n}{1} \]
Ze zadání víme, že chceme vyjádřit index lomu n pomocí \(\varphi\) a \(\psi\).

Vyjádříme si úhel \(\omega\) pomocí \(\varphi\) a \(\psi\).

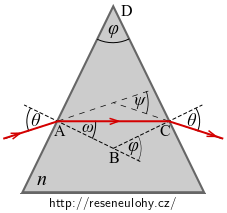
Velikost vrcholového úhlu \(\varphi\) hranolu má i vnější úhel při vrcholu B.

Vezmeme čtyřúhelník ABCD, u kterého víme, že součet vnitřních úhlů musí být 360°. Úhly u vrcholů A i C jsou pravé. Úhel u vrcholu B je \(180° - \varphi\). Díky tomu je vedlejší úhel u vrcholu B roven \(\varphi\).

Pro rovnoramenný \(\Delta ABC\) platí
\[ \varphi = \omega + \omega, \]
a odtud snadno
\[ \omega = \frac{\varphi}{2}. \]
Vyjádříme úhel \(\theta\) pomocí naměřených úhlů.

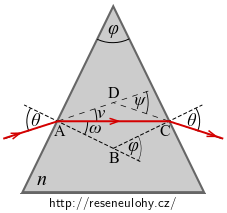
Pro úhly \(\theta, \nu, \omega\) s vrcholem v bodě \(\mathrm{A}\) platí
\[ \theta = \nu + \omega. \]
Vnější úhel \(\psi\) při vrcholu \(D\) v \(\Delta ACD\) je roven součtu vnitřních úhlů u zbývajících vrcholů. Neboť je trojúhelník rovnoramenný, platí
\[ \psi = \nu + \nu. \]
Odtud snadno
\[\nu = \frac{\psi}{2}.\]
Dosazením dostáváme
\[ \theta = \nu + \omega = \frac{\psi+\varphi}{2}. \]
Dosazením vztahů pro \(\varphi\) a \(\psi\) do vzorce pro výpočet indexu lomu \(n\) dostáváme hledaný vztah
\[ n=\frac{\sin \frac{\psi + \varphi}{2} }{\sin\frac{\varphi}{2}}. \]
Odpověď
Hledaný vztah pro výpočet indexu lomu z naměřených úhlů je
\[ n=\frac{\sin \frac{\psi + \varphi}{2} }{\sin\frac{\varphi}{2}}. \]
Odkaz na pokus
Co je to deviační úhel a kdy je tento úhel minimální? Nejen odpovědi na tyto otázky získáte provedením experimentu Lom monochromatického světla optickým hranolem ze sbírky fyzikálních pokusů!