Sbírka řešených úloh

Newtonova skla

Úloha číslo: 1632

• Nápověda 1

  Co jsou to Newtonova skla? Jaké interferenční obrazce ukazují?

• Řešení nápovědy 1

  Newtonova skla jsou jednoduchá zařízení, kterými lze pozorovat interferenci. Jsou tvořena skleněnou deskou (tzv. planparalelní deska), k níž je přiložena ploskovypuklá čočka (tj. čočka, jejíž jedna plocha je rovinná, druhá kulová), viz obrázek. Kulová plocha čočky má velký poloměr křivosti, který označíme R. V okolí místa dotyku čočky s deskou vzniká tenká vzduchová vrstvička o tloušťce d, jež se mění se vzdáleností od středu čočky. Interferenční obrazec pro monofrekvenční světlo dává střídající se světlé a tmavé kroužky, kterým se říká Newtonovy kroužky. Při použití bílého světla vznikají Newtonovy kroužky duhových barev.

  

  Na obrázku je schématický nákres, kde R je poloměr křivosti kulové části čočky, d je tloušťka vzduchové vrstvy, r_k je poloměr interferenčního kroužku, kde k je pořadové číslo kroužku – např. řád maxima. Písmena T, O, P jsou body na kružnici o poloměru R.

• Nápověda 2

  Nalezněte vztah mezi průměrem interferenčního kroužku r_k a poloměrem křivosti R a tloušťkou vzduchové vrstvy d.

• Řešení nápovědy 2

  

  Trojúhelník TOP je pravoúhlý podle Thaletovy věty, můžeme tedy použít Euklidovu větu o výšce v trojúhelníku TOP:

  \[r^\mathrm{2}_\mathrm{k}=\,d(\mathrm{2}R − d)=\,\mathrm{2}Rd − d^\mathrm{2}.\]

  Vzhledem k tomu, že d je mnohem menší než R, můžeme člen d² zanedbat a předchozí rovnici upravit na:

  \[r^\mathrm{2}_\mathrm{k}=\,\mathrm{2}Rd.\]

• Nápověda 3

  Které paprsky interferují? Jak se mění jejich fáze při odrazech? Jaký je vztah pro výpočet interferenčních maxim?

• Řešení nápovědy 3

  Při kolmém dopadu světla dochází k interferenci světla odraženého od obou rozhraní vzduchové vrstvy o tloušťce d. První paprsek se odráží na rozhraní sklo – vzduch, a tedy nemění zde svoji fázi. Druhý paprsek prochází do vzduchové vrstvy, musí tedy urazit delší optickou dráhu a navíc při odrazu od skla změní fázi, tomu odpovídá celkový dráhový rozdíl Δl:

  \[\mathrm{\Delta}l = \,\frac{\lambda}{2} + \mathrm{2}nd,\]

  kde n je index lomu vzduchové vrstvy a d je tloušťka vzduchové vrstvy.

  Detailní vysvětlení interference na tenké vrstvě najdete v úloze Vrstva oleje na vodě.

• Nápověda 4

  Co musí platit pro dráhový rozdíl, aby nastalo interferenční maximum?

• Řešení nápovědy 4

  Protože v úloze chceme spočítat, kolik světlých kroužků vznikne, potřebujeme, aby vzniklo maximum, tj. aby se paprsky potkaly s dráhovým rozdílem rovným násobku vlnové délky Δl = kλ:

  \[k\lambda=\,\mathrm{2}nd + \,\frac{\lambda}{2}.\]

  Vyjádříme si k:

  \[k=\,\frac{\mathrm{2}nd+\frac{\lambda}{2}}{\lambda},\]

  kde ovšem neznáme tloušťku vrstvy d. V předchozí nápovědě jsme si odvodili vztah pro poloměr interferenčního kroužku r_k² = 2Rd, ze kterého si vyjádříme d.

  Teď už nám zbývá jen zjistit, co dosadit za r_k. Jelikož počítáme, kolik světlých kroužků dohromady vznikne, dosadíme za r_k polovinu průměru \(\frac{p}{\mathrm{2}}\) použité čočky, jako bychom chtěli počítat poslední světlý kroužek, který vznikne na úplném konci čočky.

• Zápis

  λ = 589 nm = 5,89·10−7 m	vlnová délka světla
  nv = 1	relativní index lomu vzduchu
  nvo = 1,33	relativní index lomu vody
  p = 20 mm = 2·10−2 m	průměr čočky
  R = 5 m	poloměr křivosti čočky
  kv = ?	počet kroužků ve vzduchu
  kvo = ?	počet kroužků ve vodě

• Řešení

  Při interferenci světla na ploskovypuklé čočce položené na rovné skleněné desce vznikají pro monofrekvenční světlo světlé a tmavé kroužky, kterým se říká Newtonovy kroužky.

  

   

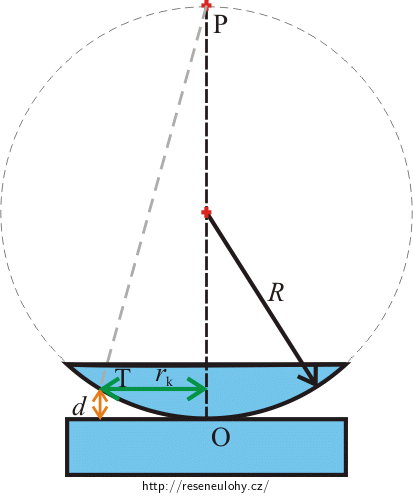
  Nejprve si vyjádříme poloměr světlého kroužku r_k pomocí poloměru křivosti čočky R a tloušťky vzduchové vrstvy d.

  

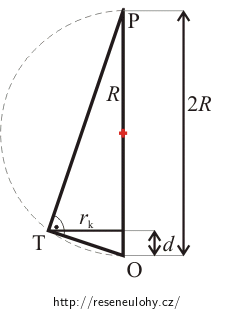
  Trojúhelníku TOP je pravoúhlý a pomocí Euklidovy věty můžeme vypočítat výšku tohoto trojúhelníku r_k, která odpovídá poloměru světlého kroužku k-tého řádu:

  \[r^\mathrm{2}_\mathrm{k}=\,d(\mathrm{2}R − d)=\,\mathrm{2}Rd − d^\mathrm{2}\dot=\,\mathrm{2}Rd.\]

  Protože d << R, můžeme člen d² zanedbat.

   

  Při kolmém dopadu světla dochází k interferenci světla odraženého od obou rozhraní vzduchové vrstvy o šířce d, tomu odpovídá celkový dráhový rozdíl Δl:

  \[\mathrm{\Delta}l = \,\frac{\lambda}{\mathrm{2}} + \mathrm{2}nd,\]

  kde n je index lomu vzduchové vrstvy a d je tloušťka vzduchové vrstvy (jeden z paprsků mění svoji fázi, detailněji viz nápověda 4).

  V úloze chceme spočítat, kolik světlých kroužků vznikne, tedy budeme počítat interferenční maxima, pro která platí vztah: Δl = kλ. Dosadíme do předchozí rovnice za Δl a vyjádříme si k:

  \[k=\,\frac{nr_\mathrm{k}^\mathrm{2}}{\lambda R}+\frac{1}{2},\]

  kde n je index lomu látky mezi čočkou a skleněnou deskou, tj. pro část a) vzduchové vrstvy n = 1 a b) vody n = 1,33, r_k je poloměr k-tého světlého kroužku a R je poloměr křivosti čočky.

  Jelikož potřebujeme vědět, kolik světlých kroužků dohromady vznikne, pokud máme čočku o průměru p, tak za r_k dosadíme polovinu průměru, jako bychom chtěli počítat poslední světlý kroužek.

  Upravíme předchozí rovnici

  \[k_\mathrm{v}=\,\frac{n\frac{p^\mathrm{2}}{\mathrm{4}}}{\lambda R}+\frac{1}{2}=\,\frac{np^\mathrm{2}}{\mathrm{4}\lambda R}+\frac{1}{2}\]

  a můžeme dosazovat hodnoty ze zadání.

   

  Část a) vzduchová vrstva n = 1:

  \[k_\mathrm{v}=\,\frac{np^\mathrm{2}}{\mathrm{4}\lambda R}+\frac{1}{2}=\,\frac{1\,\cdot\,0{,}02^\mathrm{2}}{4\,\cdot\,5{,}89{\cdot}10^{−7}\,\cdot\,5}+\frac{1}{2}\,\dot =\,\, 34.\]

  Hodnota k nám říká, kolikátý poslední vznikne kroužek, jinak řečeno, kolik kroužků vzniklo celkem.

   

  Část b) vodní vrstva n = 1,33:

  \[k_\mathrm{vo}=\,\frac{np^\mathrm{2}}{\mathrm{4}\lambda R}+\frac{1}{2}=\,\frac{1{,}33\,\cdot\,0{,}02^\mathrm{2}}{\mathrm{4}\,\cdot\, 5{,}89{\cdot}10^{−7}\,\cdot\,5}+\frac{1}{2}\,\dot=\,\,45.\]

• Odpověď

  Pokud máme Newtonova skla ve vzduchu, vznikne 34 světlých kroužků. Pokud je ponoříme do vody, vnikne 45 světlých kroužků.