Výpočet vzájemné vzdálenosti maxim
Úloha číslo: 1651
Na ohybovou mřížku, která má 100 vrypů na 1 mm, dopadá kolmo červené světlo o vlnové délce 700 nm. Určete, v jaké vzájemné vzdálenosti budou první, druhý a třetí světlý pás na stínítku ve vzdálenosti 100 cm od mřížky.
Obrázek
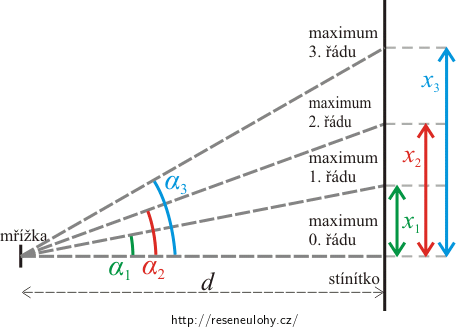
Označení na obrázku: d je vzdálenost mřížky od stínítka,
- α1 je úhel odchýlení maxima 1. řádu, α2 je úhel odchýlení maxima 2. řádu a α3 je úhel odchýlení maxima 3. řádu,
- x1 je vzdálenost maxima 1. řádu od maxima 0. řádu, x2 je vzdálenost maxima 2. řádu od maxima 0. řádu, x3 je vzdálenost maxima 3. řádu od maxima 0. řádu,
Nápověda 1
Připoměňte si, jaký vztah platí pro výpočet mřížkové konstanty pomocí počtu vrypů N.
Pokud si nejste jistí, podívejte se nejprve na úlohu Výpočet vrypů na 1 mm.
Nápověda 2
Jaký vztah platí pro úhel odchýlení αk, kde k je řád maxima, pokud si je vyjádříme pomocí dráhového rozdílu Δl a mřížkové konstanty b?
Nápověda 3
Pomocí již vypočítaného úhlů odchýlení αk vypočítejte vzdálenosti k-tého maxima xk od maxima 0. řádu.
Zápis
d = 100 cm = 1 m vzdálenost mřížky od stínítka λ = 700 nm = 7,0·10−7 m vlnová délka dopadajícího světla Δxk = ? (cm) vzájemná vzdálenost maxima k-tého řádu a maxima řádu k-1 N = 100 počet vrypů na 1 mm Řešení
V úloze chceme spočítat vzájemné vzdálenosti prvního, druhého a třetího světlého pásu, tedy Δx1, Δx2, Δx3, na stínítku.
Nakreslíme si obrázek, kde si označíme:
- d je vzdálenost mřížky od stínítka,
- α1 je úhel odchýlení maxima 1. řádu, α2 je úhel odchýlení maxima 2. řádu a α3 je úhel odchýlení maxima 3. řádu,
- x1 je vzdálenost maxima 1. řádu od maxima 0. řádu, x2 je vzdálenost maxima 2. řádu od maxima 0. řádu, x3 je vzdálenost maxima 3. řádu od maxima 0. řádu,

Pro přehlednost řešení si všechny vztahy odvodíme pro obecné k-té maximum a nakonec jen dosadíme požadované hodnoty.
Pro úhly odchýlení platí:
\[\sin\,α_\mathrm{k} = \, \frac{\mathrm{Δ}l_\mathrm{k}}{b},\]kde Δlk je dráhový rozdíl vždy dvou sousedních paprsků k-tého maxima, b je mřížková konstanta a αk je úhel, který paprsky svírají s centrální osou.
Protože se jedná o maxima, platí pro dráhový rozdíl Δl vztah Δl = kλ:
\[\sin\,α_\mathrm{k} = \, \frac{kλ}{b}.\]Z obrázku vidíme, že pro vzdálenost k-tého maxima xk od maxima 0. řádu platí vztah:
\[\mathrm{tg}\,\,α_\mathrm{k}=\,\frac{x_\mathrm{k}}{d},\]kde d je vzdálenost mřížky od stínítka.
Ze vztahu si vyjádříme vzdálenost maxim xk.
\[x_\mathrm{k}=\,d\,\mathrm{tg}\,\,α_\mathrm{k}.\]Protože se jedná o velmi malé úhly, tak pro ně platí
\[\sin\,α\ \dot{=}\ \, α\ \dot{=}\ \mathrm{tg}\,\,α,\]kde úhel je vyjádřen v radiánech.
Vypočítáme si obecně vzdálenost dvou sousedních maxim
\[\mathrm{Δ}x_\mathrm{k}=\,d\,\mathrm{tg}\,\,α_\mathrm{k} − d\,\mathrm{tg}\,\,α_\mathrm{(k − 1)}=\,\frac{d}{b}\left(kλ − (k − 1) λ\right)=\,\frac{d}{b}λ. \]Z tohoto obecného vztahu je vidět, že nám vzdálenost mezi dvěma sousedními maximy vyjde vždy stejná.
Při dosazování číselných hodnot použijeme vztah pro mřížkovou konstantu b:
\[b=\,\frac{10^\mathrm{−3}\,\mathrm{m}}{N}=\,\,\frac{10^\mathrm{−3}}{100}\,\mathrm{m}.\]Výpočet vzdálenosti dvou sousedních maxim:
\[\mathrm{Δ}x = \,d\frac{λ}{b} =\,1\,\cdot\frac{7{,}0{\cdot}10^{−7}\,\mathrm{m}}{\frac{10^\mathrm{−3}\,\mathrm{m}}{100}}=\,0{,}070\,\mathrm{m}=\,7{,}0\,\mathrm{cm}. \]Odpověď
Vzájemná vzdálenost dvou sousedních maxim je 7 cm.Komentář
Vzájemné vzdálenosti sousedních maxim nám vyšly stejné. Je to proto, že jsme použili přibližnou rovnost mezi sinem a tangentou velmi malých úhlů. Pokud bychom počítali s přesnými hodnotami, zjistili bychom, že se námi spočtené přibližné hodnoty liší jen nepatrně.
Provedeme celý výpočet bez použítí zanedbání.
Máme vztahy:
\[\sin\,α_\mathrm{k} = \, \frac{kλ}{b} \quad\Rightarrow\quad α_\mathrm{k}=\,\arcsin\, \frac{kλ}{b}.\]Pomocí funkce tangens dostaneme vztah:
\[\mathrm{tg}\,\,α_\mathrm{k}=\,\frac{x_\mathrm{k}}{d},\]ze kterého si vyjádříme xk a za α si dosadíme z předchozí rovnice:
\[x_\mathrm{k}=\,d\,\mathrm{tg}\,\,\arcsin\, \frac{kλ}{b}.\]Získali jsme vztah pro polohu maxim. Teď si vypočítáme jejich vzájemnou vzdálenost.
Využijeme obecný vztah, do kterého si postupně budeme dosazovat.
\[\mathrm{Δ}x_\mathrm{k}=\,d\,\mathrm{tg}\,\,α_\mathrm{k} − d\,\mathrm{tg}\,\,α_\mathrm{(k − 1)}.\]Vztah pro výpočet b je:
\[b=\,\frac{10^\mathrm{-3}\,\mathrm{m}}{N}=\,\frac{10^\mathrm{-3}}{100}\,\mathrm{m}.\]Výpočet vzdálenosti maxima 1. řádu od maxima 0. řádu:
\[\mathrm{Δ}x_\mathrm{1}=\,d\,\mathrm{tg}\,\,α_\mathrm{1}=\,d\,\mathrm{tg}\,\,\arcsin \,\frac{1λ}{b}=\] \[=\,1\cdot\,\mathrm{tg}\,\,\arcsin \,\frac{1{\cdot}7{,}0{\cdot}10^{-7}}{\frac{10^\mathrm{-3}}{100}}\mathrm{m}\,\dot=\,0{,}07\,\mathrm{m}\,=\,7{,}0\,\mathrm{cm}.\]Výpočet vzájemné vzdálenosti maxima 1. řádu a 2. řádu:
\[\mathrm{Δ}x_\mathrm{2}=\,d\left(\mathrm{tg}\,\,α_\mathrm{2} − \mathrm{tg}\,\,α_\mathrm{1}\right)=\,d\left(\mathrm{tg}\,\,\arcsin \,\frac{2λ}{b} − \mathrm{tg}\,\,\arcsin \,\frac{1λ}{b}\right)=\] \[=\,1\cdot\left(\mathrm{tg}\,\,\arcsin \,\frac{2{\cdot}7{,}0{\cdot}10^{-7}}{\frac{10^\mathrm{-3}}{100}} − \mathrm{tg}\,\,\arcsin \,\frac{1{\cdot}7{,}0{\cdot}10^{-7}}{\frac{10^\mathrm{-3}}{100}}\right)\,\mathrm{m}\,\dot=\,0{,}071\,\mathrm{m}\,=\] \[=\,7{,}1\,\mathrm{cm}.\]Výpočet vzájemné vzdálenosti maxima 2. řádu a 3. řádu:
\[\mathrm{Δ}x_\mathrm{3}=\,d\left(\mathrm{tg}\,\,α_\mathrm{3} − \mathrm{tg}\,\,α_\mathrm{2}\right)=\,d\left(\mathrm{tg}\,\,\arcsin \,\frac{3λ}{b} − \mathrm{tg}\,\,\arcsin \,\frac{2λ}{b}\right)=\] \[=\,1\cdot\left(\mathrm{tg}\,\,\arcsin \,\frac{3{\cdot}7{,}0{\cdot}10^{-7}}{\frac{10^\mathrm{-3}}{100}} − \mathrm{tg}\,\,\arcsin \,\frac{2{\cdot}7{,}0{\cdot}10^{-7}}{\frac{10^\mathrm{-3}}{100}}\right)\,\mathrm{m}\,\dot=\,0{,}073\,\mathrm{m}\,=\] \[=\,7{,}3\,\mathrm{cm}.\]


