Drozd a žížala
Úloha číslo: 1907
Drozd vytahuje žížalu svisle vzhůru z jamky zalité vodou. Zdá se mu, že už zbývá vytáhnout jen kousek žížaly, reálně však musí vytáhnout její polovinu. Celková délka žížaly je \(d\), zdánlivá délka části žížaly, kterou drozd vidí pod vodou, je \(z\). Určete poměr \(\frac{z}{d}\).
Zápis
\(d\) délka žížaly \(d_{v}=\frac{1}{2}d\) délka žížaly, která je ještě pod vodou (neboli vzdálenost od hladiny vody ke konci žížaly pod vodou)
\(z\) vzdálenost od hladiny vody ke zdánlivému konci žížaly pod vodou (zdánlivá délka části žížaly, kterou drozd vidí pod vodou) \(\frac{z}{d}= ?\) poměr zdánlivé délky části žížaly, která je pod vodou a délky žížaly Nápověda 1
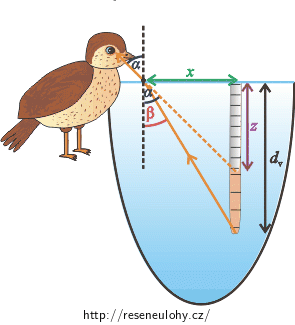
Nakreslete obrázek ukazující, jak paprsek dopadá od konce žížaly do oka drozda. Znázorněte, jak se paprsek na rozhraní voda-vzduch láme. Pro lepší názornost zakreslete obrázek tak, že se drozd nebude na žížalu dívat přímo shora. Do obrázku vyznačte, kde drozd uvidí zdánlivý konec žížaly. Obrázek popište.
Nápověda 2
Napište Snellův zákon lomu.
Nápověda 3
Uvědomte si nebo vyhledejte, co je to tzv. paraxiální aproximace.
Nápověda 4
Vraťte se k obrázku z nápovědy 1. Uvědomte si, že \(z\) svírá s protaženým paprsek také úhel \(α\).
V předchozí nápovědě jsme zjistili, že v zákonu lomu můžeme v našem případě psát tangens místo sinus. To se nám hodí, protože \(\mathrm{tg}\,{α}\) a \(\mathrm{tg}\,{β}\) se nám budou z obrázku lépe vyjadřovat.
V obrázku najděte a vyznačte dva pravoúhlé trojúhelníky s jejichž pomocí můžete vyjádřit \(\mathrm{tg}\,{α}\) a \(\mathrm{tg}\,{β}\).
Nápověda 5
Užitím odvozených vztahů určete, čemu odpovídá zdánlivá délka ponořené části žížaly \(z\).
Celkové řešení
Nakreslíme obrázek ukazující, jak paprsek dopadá od konce žížaly do oka drozda. Pro lepší názornost zakreslíme obrázek tak, že se drozd nebude na žížalu dívat přímo shora.
Paprsek dopadá od žížaly na hladinu vody pod úhlem \(β\), kde se láme a dopadá do oka drozda pod úhlem \(α\). Tento paprsek se řídí zákonem lomu: \[n_{1}\sin α=n_{2}\sin β,\tag{1}\] kde \( n_{1}\) je index lomu vzduchu a \(n_{2}\) je index lomu vody.
Protažením paprsku, který dopadá do oka drozda, můžeme zakreslit zdánlivý obraz konce žížaly.
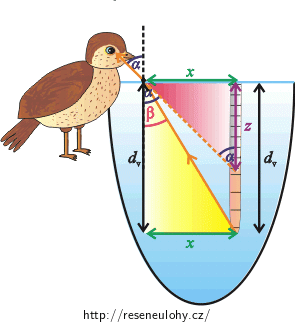
\(d_{v}\) je vzdálenost od hladiny vody ke konci žížaly pod vodou, \(z\) je vzdálenost od hladiny vody ke zdánlivému konci žížaly pod vodou a \(x\) je vzdálenost mezi místem, kde se paprsek láme na hladině a kolmým průmětem žížaly na hladinu.
Využijeme paraxiální aproximace (viz nápověda 3): \[\sin {α} = \mathrm{tg}\, {α},\tag{2}\] \[\sin {β}= \mathrm{tg}\, {β}.\tag{3}\]
Z červeného trojúhelníku určíme: \[\mathrm{tg}\, {α}=\frac{x}{z}. \tag{4}\] Ze žlutého trojúhelníku můžeme odvodit: \[\mathrm{tg}\, {β}=\frac{x}{d_{v}}. \tag{5}\]
Vztahy (2) a (3) dosadíme do rovnice pro zákon lomu (1): \[n_{1}\mathrm{tg}\,α=n_{2}\mathrm{tg}\, β.\] Do rovnice dosadíme vztahy (4) a (5): \[n_{1}\frac{x}{z}=n_{2}\frac{x}{d_{v}}.\] Vyjádříme \(z\): \[n_{1}\frac{1}{z}=n_{2}\frac{1}{d_{v}},\] \[n_{1}d_{v}=n_{2}z,\] \[z=\frac{n_{1}}{n_{2}}d_{v}.\] Dosadíme za \(d_{v}\) dle zápisu \(d_{v}=\frac{1}{2}d\): \[z=\frac{n_{1}}{n_{2}}\frac{1}{2}d,\] \[z=\frac{n_{1}}{2n_{2}}d.\]
V tabulkách dohledáme hodnotu indexu lomu vzduchu \(n_{1}\) a vody \(n_{2}\):
\(n_{1}\) \(=\) \(1{,}00\)
\(n_{2}\) \(=\) \(1{,}33\)
Dosadíme:
\(z=\frac{n_{1}}{2n_{2}}d=\frac{1}{2{\cdot}1{,}33}d \dot= 0{,}4d.\)
Odtud \(\frac{z}{d} \dot= 0{,}4.\)
Drozd už vytáhnul polovinu žížaly a pod vodou vidí část žížaly o délce \(z\), proto se mu zdá, že žížala má délku: \(0{,}5d+0{,}4d = 0{,}9d\). Reálně však má žížala délku \(d\). Drozdovi se tedy zdá, že žížala je přibližně o desetinu kratší než ve skutečnosti.
Odpověď
Pro zdánlivou délku potopené části žížaly platí \(z \dot= 0{,}4d\). (Tedy \(\frac{z}{d}\dot= 0{,}4\).)
To znamená, že se drozdovi zdá, že žížala je přibližně o desetinu kratší než ve skutečnosti.