Zvětšení mikroskopu
Úloha číslo: 1901
Mikroskop má příčné zvětšení objektivu \(30\), úhlové zvětšení okuláru \(5\) a optický interval mikroskopu je \(15 \mathrm{cm}\). Určete zvětšení mikroskopu, jestliže předmět pozorujeme okem bez akomodace. Dále určete ohniskové vzdálenosti objektivu a okuláru.
Zápis
\(Z_{1}= 30\) příčné zvětšení objektivu \(γ_{2}=5\) úhlové zvětšení okuláru \(Δ=15 \mathrm{cm}= 0{,}15 \mathrm{m}\) optický interval mikroskopu \(γ= ?\) zvětšení mikroskopu \(f_{1}= ?\) ohnisková vzdálenost objektivu \(f_{2}= ?\) ohnisková vzdálenost okuláru Nápověda 1
Z čeho se mikroskop skládá a jak funguje?
Nápověda 2
Jaký je vztah mezi celkovým zvětšením mikroskopu \(γ\), příčným zvětšením objektivu \(Z_{1}\) a úhlovým zvětšením okuláru \(γ_{2}\)?
Nápověda 3
Co je optický interval \( Δ\)?
Nápověda 4
Odvoďte vztah pro příčné zvětšení objektivu. Následně určete ohniskovou vzdálenost objektivu.
Nápověda 5
Co je úhlové zvětšení okuláru? Jak ho vypočítáme? Určete ohniskovou vzdálenost okuláru.
Celkové řešení
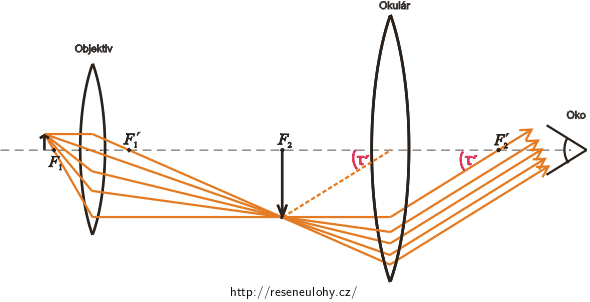
Obrázek mikroskopu
Mikroskop se skládá ze dvou spojných čoček (objektiv a okulár).
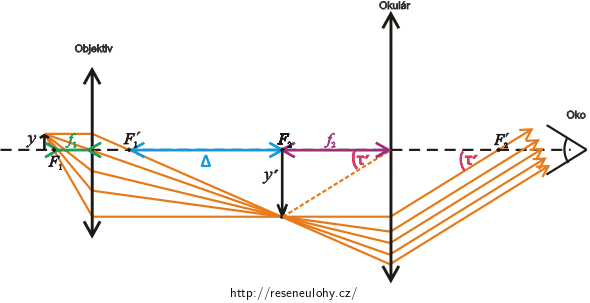
Popis obrázku
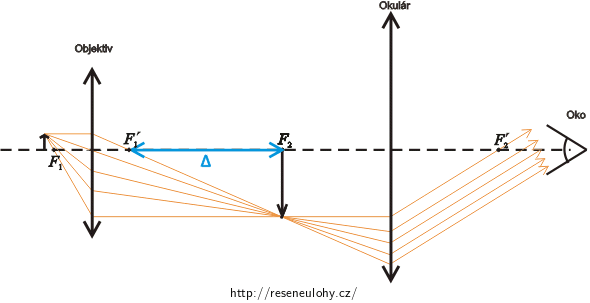
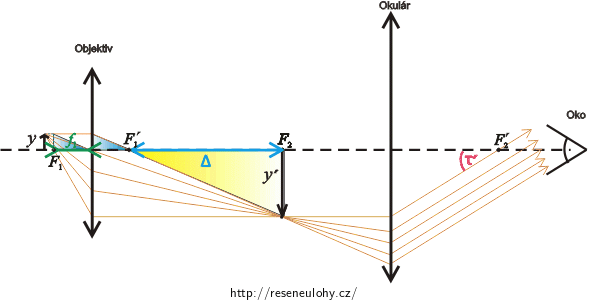
\(F_{1}\) předmětové ohnisko objektivu\(y\)výška předmětu\(F'_{1}\) obrazové ohnisko objektivu\(y'\)výška obrazu vytvořeného objektivem\(F_{2}\) předmětové ohnisko okuláru\(f_{1}\)ohnisková vzdálenost objektivu\(F'_{2}\) obrazové ohnisko okuláru\(f_{2}\)ohnisková vzdálenost okuláru\(τ'\) zvětšený zorný úhel\(Δ\)optický intervalCelkové zvětšení mikroskopu
Celkové zvětšení mikroskopu získáme jako součin příčného zvětšení objektivu a úhlového zvětšení okuláru. Tedy: \[γ=Z_{1}\cdot γ_{2}\tag{1}\]
Příčné zvětšení objektivu a jeho ohnisková vzdálenost
Příčné zvětšení objektivu \( Z_{1}\) popisuje, kolikrát je obraz vytvořený objektivem větší než zobrazovaný předmět, proto platí vztah: \[Z_{1}=\frac{y'}{y},\tag{2}\] kde \(y'\) je výška obrazu a \(y\) je výška předmětu.
Určíme, čemu odpovídá poměr výšky obrazu a předmětu.
Žlutý trojúhelník je podobný modrému trojúhelníku. Z této podobnosti vyplývá: \[\frac{y'}{Δ}=\frac{y}{f_{1}},\] kde \(f_{1}\) je ohnisková vzdálenost objektivu. Vyjádříme poměr výšky předmětu a obrazu: \[\frac{y'}{y}= \frac{Δ}{f_{1}}.\] A dle (2): \[Z_{1}= \frac{Δ}{f_{1}}.\] Odtud vyjádříme ohniskovou vzdálenost objektivu: \[f_{1}= \frac{Δ}{Z_{1}}.\tag{3}\]
Úhlové zvětšení okuláru a jeho ohnisková vzdálenost
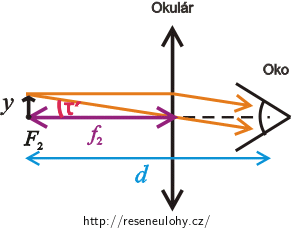
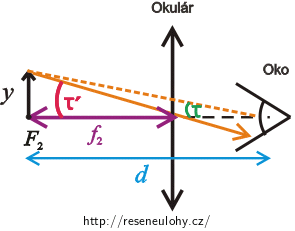
Okulár mikroskopu funguje jako lupa. Platí vztah: \[γ_{2}=\frac{τ'}{τ}.\tag{4}\]
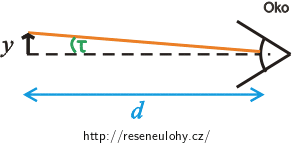
Nakreslíme obrázek, ze kterého určíme velikost zorného úhlu \(τ\), pod kterým pozorujeme pouhým okem předmět o výšce \(y\) z konvenční zrakové vzdálenosti \(d\) .
Nyní mezi předmět a oko vložíme okulár tak, že předmět bude umístěn v předmětovém ohnisku okuláru. Úhel, pod kterým budeme pozorovat předmět, se zvětší (zvětšený zorný úhel \(τ'\)).
Z obrázku odvodíme, že pokud budeme pozorovat předmět pouhým okem, pak bude platit: \[\mathrm{tg}\,{τ}=\frac{y}{d}.\] Protože úhel \(τ\) je velmi malý, můžeme říci, že \(\mathrm{tg}\,{τ} \dot= τ\) a proto můžeme psát: \[τ=\frac{y}{d}.\tag{5}\]
Pozorujeme-li předmět skrz okulár, můžeme odvodiv vztah pro zvětšený zorný úhel \(τ'\): \[\mathrm{tg}\,{τ'}=\frac{y}{f_{2}}.\] Zvětšený zorný úhel je malý a proto můžeme psát: \[τ'=\frac{y}{f_{2}}.\tag{6}\]
Dosadíme vztah (5) a (6) do vztahu pro úhlové zvětšení okuláru (4) a upravíme:
\[γ_{2}=\frac{τ'}{τ}=\frac{\frac{y}{f_{2}}}{\frac{y}{d}},\] \[γ_{2}=\frac{d}{f_{2}}.\]
Vyjádříme ohniskovou vzdálenost okuláru: \[f_{2}=\frac{d}{γ_{2}}.\tag{7}\]
Číselné řešení
Ze zadání víme:
\(Z_{1}=30\)
\(γ_{2}=5\)
\(Δ=0{,}15 \mathrm{m}\)
V tabulkách dohledáme konvenční zrakovou vzdálenost:
\(d= 0{,}25 \mathrm{m}\)
Dosazujeme do vztahů:
pro celkové zvětšení mikroskopu (1):
\(γ=Z_{1} \cdot γ_{2} = 30 {\cdot} 5=150.\)
pro ohniskovou vzdálenost objektivu (3):
\(f_{1}= \frac{Δ}{Z_{1}}=\frac{0{,}15}{30} \mathrm{m}=5{\cdot}10^{−3} \mathrm{m}=5 \mathrm{mm}.\)
pro ohniskovou vzdálenost okuláru (7):
\(f_{2}=\frac{d}{γ_{2}}=\frac{0{,}25}{5} \mathrm{m}=5{\cdot}10^{−2} \mathrm{m}=50 \mathrm{mm}.\)
Odpověď
Zvětšení mikroskopu je \(150\). Ohnisková vzdálenost objektivu je \(5 \mathrm{mm}\) a okuláru \(50 \mathrm{mm}\).