Ohyb na dvojité štěrbině

Úloha číslo: 1505

Stanovte průběh intenzity světla na stínítku při Youngově interferenčním pokusu. Vzdálenost obou štěrbin šířky \(d\) je \(b\). Stínítko je umístěno ve vzdálenosti \(l\), přičemž \(l\gg b+d\).

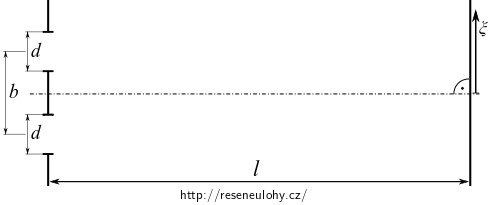
Do výpočtu zahrňte vliv ohybového jevu na štěrbině nezanedbatelné šířky.
Na štěrbiny dopadá kolmo rovinná harmonická vlna, lineárně polarizovaná ve směru štěrbin.
Řešte v aproximaci Fraunhoferova obybu.

Elektrickou intenzitu v daném místě stínítka určete integrací příspěvků od zdrojů přes průřez štěrbin. Použijte vyjdáření v komplexním formalismu.

Odkazy na související úlohy
Před řešením této úlohy doporučujeme prostudovat úlohu Ohyb na štěrbině, která je jednodušší variantou této úlohy.

Youngův interferenční pokus bez uvažování ohybu na štěrbinách naleznete v úloze Youngův pokus.

Tato úloha lze řešit bez integrace superpozicí vln ze dvou samostatných štěrbin, viz Ohyb na dvojité štěrbině alternativně. Tento přístup ovšem přebírá výsledky z úlohy Ohyb na štěrbině.
Teorie a vztahy potřebné pro řešení úlohy
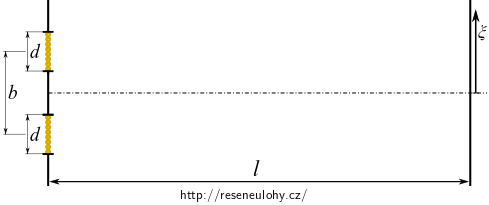
Obě štěrbiny nezanedbatelné šířky lze modelovat jako spojité pásy přímkových zdrojů válcových vln.

Pás přímkových zdrojů je na obrázku znázorněn úsečkou kolmých žlutých průmětů.

Elektrickou intenzitu válcové vlny lze popsat funkcí
\[ E(\rho) = \frac{\mathcal{E}_0}{\sqrt{\rho}}e^{i(\omega t - k\rho)}. \]
Do dané linie stínítka přicházejí válcové vlny z různých částí štěrbin s různými souřadnicemi \(\rho\) a superponují. Výslednou elektrickou intenzitu nalezneme integrací přímkových zdrojů přes průřezy štěrbin.

Je-li stínítko dostatečně daleko, lze části válcových vlnoploch považovat za téměř rovinné a pro výpočet intenzity světla užít vztah platný pro rovinnou vlnu
\[ I = \frac{1}{2z_0} EE^\star, \]
kde \(z_0 = \sqrt{\frac{\mu_0}{\varepsilon_0}}\) značí charakteristickou impedanci vakua.
Integrál potřebný k výpočtu
Při řešení se bude hodit integrál exponenciální funkce s multiplikativní konstantou v argumentu
\[ \int e^{\varphi x}\,\mathrm{d}x = \frac{e^{\varphi x}}{\varphi} + C. \]
Nápověda 1 – superpozice elektrických intenzit
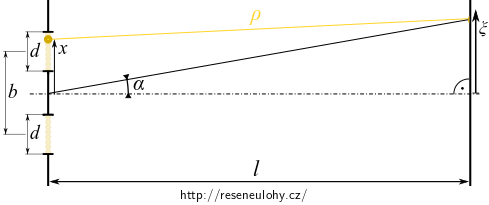
Napište vyjádření válcové vlny dílčího přímkového zdroje na souřadnici \(x\).

Vyjádřete souřadnici \(\rho\) pomocí vzdálenosti \(l\), souřadnice \(x\) myšleného přímkového zdroje a souřadnice místa na stínítku \(\xi\). Výraz upravte s uvážením \(x \lt d\ll l\).

Výsledná elektrická intenzita je dána součtem dílčích příspěvků od všech přímkových zdrojů štěrbiny. Ty ji pokrývají spojitě, sestavte tedy příslušný integrál.
Řešení nápovědy 1 – superpozice elektrických intenzit
Příspěvek k elektrické intenzitě na stínítku v místě o souřadnici \(\xi\), příslušící elementárnímu zdroji šířky \(\mathrm{d}x\) na souřadnici \(x\) štěrbiny, je
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{\rho}} e^{i(\omega t - k\rho)} \mathrm{d}x, \tag{1}\]
kde \(E_0\) je konstanta (\([E_0]=\mathrm{V}\cdot\mathrm{m^{-\frac{3}{2}}}\)) a \(\rho\) je vzdálenost linie na stínítku od přímkového zdroje a lze vyjádřit pomocí \(l,\xi, x\) jako
\[ \rho = \sqrt{l^2 + (\xi-x)^2}. \tag{2}\]
Nyní provedeme dvě aproximace:
1. Zanedbání změny úbytku amplitudy v rámci stínítka.
  
  Ve vztahu (1) klesá amplituda elektrické intenzity s \(\sqrt\rho\). Je-li stínítko dostatečně daleko, jsou rozdíly \(\rho\) a tedy i rozdíly globální amplitudy zanedbatelné a proměnný výraz \(\frac{1}{\sqrt\rho}\) můžeme aproximovat konstantou \(\frac{1}{\sqrt{l}}\) To nám umožní v budoucnu snadno integrovat.
2. Úpravu \(\rho\) s přihlédnutím k \(|x| \lt d \ll l\).
  
  Upravme výraz pro \(\rho\)
  \[ \rho = \sqrt{l^2 + (\xi-x)^2} = \sqrt{l^2 + \xi^2 - 2\xi x + x^2} = \] \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{grey}{\frac{x^2}{l^2 + \xi^2}}}= \]
  Šedý člen vypustíme, je pro velká \(l\) řádově zanedbatelný a místo něj vřadíme zanedbatelně malý člen (modře) k úpravě na čtverec.
  \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{blue}{\frac{\xi^2 x^2}{\left(l^2 + \xi^2\right)^2}}}= \] \[ = \sqrt{l^2 + \xi^2}\bigg(1-\frac{\xi x}{l^2 + \xi^2} \bigg)= \] \[ = \sqrt{l^2 + \xi^2}-x\overbrace{\frac{\xi}{\sqrt{l^2 + \xi^2}}}^{\sin \alpha} =\sqrt{l^2 + \xi^2} - x\sin \alpha. \]
Předchozí aproximace nám dávají následující tvar elektrické intenzity
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{l}} e^{i(\omega t - k\rho)}\mathrm{d}x, \qquad \mathrm{kde\,} \rho = \sqrt{l^2 + \xi^2} - x\sin \alpha. \]
Celková elektrická intenzita na souřadnici \(\xi\) stínítka je dána součtem příspěvků intenzit ode všech přímkových zdrojů štěrbin. Tedy
\[ E(\xi) = \int\limits_{\mathrm{1.\,štěr.}}\! \mathrm{d}E_x(\xi) + \int\limits_{\mathrm{2.\,štěr.}}\! \mathrm{d}E_x(\xi)= \] \[ =\int\limits_{\frac{b}{2}-\frac{d}{2}}^{\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x + \int\limits_{-\frac{b}{2}-\frac{d}{2}}^{-\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]
Nápověda 2 – výpočet integrálu
Určete oba integrály, dávající v součtu průběh \(E(\xi)\)
\[ \underbrace{ \int\limits_{\frac{b}{2}-\frac{d}{2}}^{\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x }_{\mathrm{ozn.\,}\iota_1} + \underbrace{ \int\limits_{-\frac{b}{2}-\frac{d}{2}}^{-\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. }_{\mathrm{ozn.\,}\iota_2} \]
Oba integrály mají stejný integrand, liší se pouze známenky v mezích. Vypočítejte tedy integrály \(\iota_1,\iota_2\) současně a nakonec výsledky sečtěte.

Exponenciálu rozepište v součin exponenciálních funkcí, členy nezávisející na integrační proměnné \(x\) „vytkněte“ před integrál. Exponenciálu pak snadno vyintegrujete, neboť se integruje „pěkně“, tj. \(\int e^{\varphi x}\,\mathrm{d}x = \frac{e^{\varphi x}}{\varphi}+C\). Dosaďte meze a výsledek upravte.

K nalezené funkci \(E(\xi)\) určete její komplexní sdružení \(E^\star(\xi)\).
Řešení nápovědy 2 – výpočet integrálu
Oba integrály \(\iota_1, \iota_2\) vypočítáme současně
\[ \iota_{1{,}2} = \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x = \] \[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! e^{ikx\sin \alpha}\,\mathrm{d}x = \]
Konstantu jsme vytkli před integrál. Nyní nalezneme primitivní funkci.
\[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left[ \frac{e^{ikx\sin \alpha}}{ik\sin\alpha} \right]_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{\pm ik\frac{b}{2}\sin \alpha}e^{ik\frac{d}{2}\sin \alpha} - e^{\pm ik\frac{b}{2}\sin \alpha}e^{-ik\frac{d}{2}\sin \alpha} \right)= \]
V předchozím kroku jsme dosadili meze. Nyní vytkněme společnou exponenciálu.
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{ik\frac{d}{2}\sin \alpha} - e^{-ik\frac{d}{2}\sin \alpha} \right) e^{\pm ik\frac{b}{2}\sin \alpha} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) e^{\pm i\phi}, \]
kde jsme označili \(\psi = k\frac{d}{2}\sin \alpha\) a \(\phi=k\frac{b}{2}\sin \alpha\).

Průběh elektrické intenzity je součtem integrálu \( \iota_1, \iota_2\), tj.
\[ E(\xi) = \iota_1 + \iota_2 = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) \left(e^{i\phi} + e^{-i\phi}\right). \]

Samostatně upravíme obě závorky s komplexními exponenciálami. Převedeme je do goniometrického tvaru (\(e^{i\varphi} = \cos \varphi + i \sin \varphi\)).
\[ \small e^{i\psi} - e^{-i\psi} = \cos \psi + i\sin \psi - \cos( -\psi) - i\sin (-\psi) = 2i\sin\psi, \] \[ \small e^{i\phi} + e^{-i\phi} = \cos \phi + i\sin \phi + \cos( -\phi) + i\sin (-\phi) = 2\cos\phi. \]

Máme tedy
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} 2i\sin\psi \, 2\cos\phi = \] \[ = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi. \]
kde jsme za \(\sin\alpha\) dosadili ze substitučního vztahu \(\psi = k\frac{d}{2}\sin \alpha\) výraz \(\frac{2\psi}{kd}\).

K právě určené elektrické intenzitě
\[ E(\xi) = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi, \tag{3}\]
napíšeme její komplexní sdružení
\[ E^\star(\xi)= \frac{2 E_0 d}{\sqrt{l}} e^{-i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi. \tag{4}\]
Nápověda 3 – průběh intenzity na stínítku
Ve velké vzdálenosti od štěrbiny lze části válcových vln považovat za rovinné a intenzitu světla tak lze vypočítat pomocí vztahu
\[ I = \frac{1}{2z_0} EE^\star. \]
Řešení nápovědy 3 – průběh intenzity na stínítku
Průběh intenzity světla získáme dosazením (3) a (4) do vztahu pro intenzitu
\[ I = \frac{1}{2z_0} EE^\star= \overbrace{\frac{2E_0^2 d^2}{z_0l}}^{\mathrm{ozn.\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi. \]
Průběh intenzity je tedy
\[ \begin{array}{cl} I = I_0 \color{green}{\frac{\sin^2 \psi}{\psi^2}}\color{blue}{\cos^2 \phi}, \qquad \mathrm{kde}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha. \end{array} \]
Vidíme, že průběh je součinem dvou funkcí:
- \(\color{green}{\frac{\sin^2 \psi}{\psi^2}}\), kterou jsme vypočítali v příkladě pro ohyb na štěrbině,
- \(\color{blue}{\cos^2 \phi}\), kterou jsme vypočítali v příkladě s interferencí na dvojštěrbině.
Součinem obou zakreslených funkcí dostáváme průběh intenzity na následujícím obrázku.
CELKOVÉ ŘEŠENÍ
Příspěvek k elektrické intenzitě na stínítku v místě o souřadnici \(\xi\), příslušící elementárnímu zdroji šířky \(\mathrm{d}x\) na souřadnici \(x\) štěrbiny, je
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{\rho}} e^{i(\omega t - k\rho)} \mathrm{d}x, \tag{1}\]
kde \(E_0\) je konstanta (\([E_0]=\mathrm{V}\cdot\mathrm{m^{-\frac{3}{2}}}\)) a \(\rho\) je vzdálenost linie na stínítku od přímkového zdroje a lze vyjádřit pomocí \(l,\xi, x\) jako
\[ \rho = \sqrt{l^2 + (\xi-x)^2}. \tag{2}\]
Nyní provedeme dvě aproximace:
1. Zanedbání změny úbytku amplitudy v rámci stínítka.
  
  Ve vztahu (1) klesá amplituda elektrické intenzity s \(\sqrt\rho\). Je-li stínítko dostatečně daleko, jsou rozdíly \(\rho\) a tedy i rozdíly globální amplitudy zanedbatelné a proměnný výraz \(\frac{1}{\sqrt\rho}\) můžeme aproximovat konstantou \(\frac{1}{\sqrt{l}}\) To nám umožní v budoucnu snadno integrovat.
2. Úpravu \(\rho\) s přihlédnutím k \(|x| \lt d \ll l\).
  
  Upravme výraz pro \(\rho\)
  \[ \rho = \sqrt{l^2 + (\xi-x)^2} = \sqrt{l^2 + \xi^2 - 2\xi x + x^2} = \] \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{grey}{\frac{x^2}{l^2 + \xi^2}}}= \]
  Šedý člen vypustíme, je pro velká \(l\) řádově zanedbatelný a místo něj vřadíme zanedbatelně malý člen (modře) k úpravě na čtverec.
  \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{blue}{\frac{\xi^2 x^2}{\left(l^2 + \xi^2\right)^2}}}= \] \[ = \sqrt{l^2 + \xi^2}\bigg(1-\frac{\xi x}{l^2 + \xi^2} \bigg)= \] \[ = \sqrt{l^2 + \xi^2}-x\overbrace{\frac{\xi}{\sqrt{l^2 + \xi^2}}}^{\sin \alpha} =\sqrt{l^2 + \xi^2} - x\sin \alpha. \]
Předchozí aproximace nám dávají následující tvar elektrické intenzity
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{l}} e^{i(\omega t - k\rho)}\mathrm{d}x, \qquad \mathrm{kde\,} \rho = \sqrt{l^2 + \xi^2} - x\sin \alpha. \]
Celková elektrická intenzita na souřadnici \(\xi\) stínítka je dána součtem příspěvků intenzit ode všech přímkových zdrojů štěrbin. Tedy
\[ E(\xi) = \int\limits_{\mathrm{1.\,štěr.}}\! \mathrm{d}E_x(\xi) + \int\limits_{\mathrm{2.\,štěr.}}\! \mathrm{d}E_x(\xi)= \] \[ =\int\limits_{\frac{b}{2}-\frac{d}{2}}^{\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x + \int\limits_{-\frac{b}{2}-\frac{d}{2}}^{-\frac{b}{2}+\frac{d}{2}} \!\frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]
Oba integrály \(\iota_1, \iota_2\) vypočítáme současně
\[ \iota_{1{,}2} = \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x = \] \[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \int\limits_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} \! e^{ikx\sin \alpha}\,\mathrm{d}x = \]
Konstantu jsme vytkli před integrál. Nyní nalezneme primitivní funkci.
\[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left[ \frac{e^{ikx\sin \alpha}}{ik\sin\alpha} \right]_{\pm\frac{b}{2}-\frac{d}{2}}^{\pm\frac{b}{2}+\frac{d}{2}} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{\pm ik\frac{b}{2}\sin \alpha}e^{ik\frac{d}{2}\sin \alpha} - e^{\pm ik\frac{b}{2}\sin \alpha}e^{-ik\frac{d}{2}\sin \alpha} \right)= \]
V předchozím kroku jsme dosadili meze. Nyní vytkněme společnou exponenciálu.
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{ik\frac{d}{2}\sin \alpha} - e^{-ik\frac{d}{2}\sin \alpha} \right) e^{\pm ik\frac{b}{2}\sin \alpha} = \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) e^{\pm i\phi}, \]
kde jsme označili \(\psi = k\frac{d}{2}\sin \alpha\) a \(\phi=k\frac{b}{2}\sin \alpha\).

Průběh elektrické intenzity je součtem integrálu \( \iota_1, \iota_2\), tj.
\[ E(\xi) = \iota_1 + \iota_2 = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{i\psi} - e^{-i\psi} \right) \left(e^{i\phi} + e^{-i\phi}\right). \]

Samostatně upravíme obě závorky s komplexními exponenciálami. Převedeme je do goniometrického tvaru (\(e^{i\varphi} = \cos \varphi + i \sin \varphi\)).
\[ \small e^{i\psi} - e^{-i\psi} = \cos \psi + i\sin \psi - \cos( -\psi) - i\sin (-\psi) = 2i\sin\psi, \] \[ \small e^{i\phi} + e^{-i\phi} = \cos \phi + i\sin \phi + \cos( -\phi) + i\sin (-\phi) = 2\cos\phi. \]

Máme tedy
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} 2i\sin\psi \, 2\cos\phi = \] \[ = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi. \]
kde jsme za \(\sin\alpha\) dosadili ze substitučního vztahu \(\psi = k\frac{d}{2}\sin \alpha\) výraz \(\frac{2\psi}{kd}\).

K právě určené elektrické intenzitě
\[ E(\xi) = \frac{2 E_0 d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi, \tag{3}\]
napíšeme její komplexní sdružení
\[ E^\star(\xi)= \frac{2 E_0 d}{\sqrt{l}} e^{-i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin \psi}{\psi} \cos \phi. \tag{4}\]
Průběh intenzity světla získáme dosazením (3) a (4) do vztahu pro intenzitu
\[ I = \frac{1}{2z_0} EE^\star= \overbrace{\frac{2E_0^2 d^2}{z_0l}}^{\mathrm{ozn.\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi. \]
Průběh intenzity je tedy
\[ \begin{array}{cl} I = I_0 \color{green}{\frac{\sin^2 \psi}{\psi^2}}\color{blue}{\cos^2 \phi}, \qquad \mathrm{kde}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha. \end{array} \]
Vidíme, že průběh je součinem dvou funkcí:
- \(\color{green}{\frac{\sin^2 \psi}{\psi^2}}\), kterou jsme vypočítali v příkladě pro ohyb na štěrbině,
- \(\color{blue}{\cos^2 \phi}\), kterou jsme vypočítali v příkladě s interferencí na dvojštěrbině.
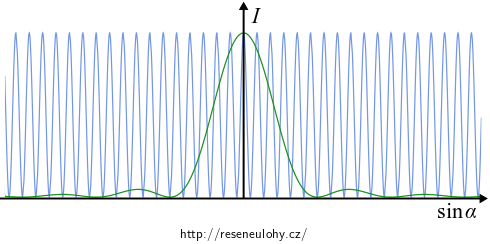
Součinem obou zakreslených funkcí dostáváme průběh intenzity na následujícím obrázku.
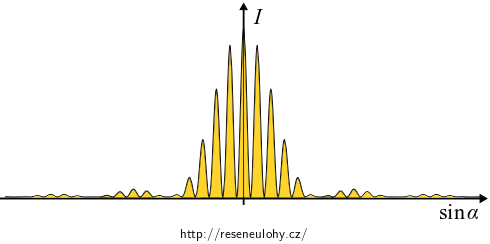
Odpověď
Průběh intenzity na stínítku je
\[ \begin{array}{cl} I = I_0 \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi, \qquad \mathrm{kde}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha, \\ & I_0 = \frac{2E_0^2 d^2}{z_0l}. \end{array} \]
Odkaz na pokus
Pokud vás zajímá, jak vypadá interferenční obrazec na stínítku ve skutečnosti, podívejte se na Dvojštěrbinový pokus.