Tučňák pozorující rybu, která plave pod ledem
Úloha číslo: 1909
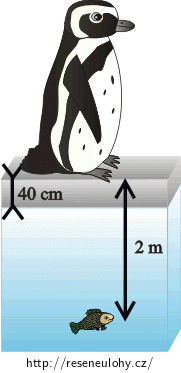
Tučňák pozoruje malou rybku, která plave v hloubce \(2 \mathrm{m}\) pod hladinou. V jaké hloubce vidí tučňák rybu, pokud je hladina vody zamrzlá do hloubky \(40 \mathrm{cm}\)?
Poznámka: Budeme předpokládat, že se tučňák dívá na rybu shora.
Zápis
\(h=2 \mathrm{m}\) hloubka, ve které plave ryba \(d=40 \mathrm{cm}=0{,}4 \mathrm{m}\) tloušťka zamrzlé hladiny \(x= ?\) hloubka, ve které tučňák uvidí rybu Nápověda 1
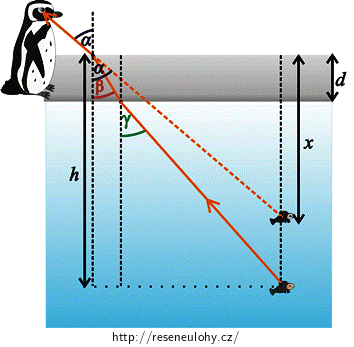
Nakreslete obrázek ukazující, jak paprsek dopadá od ryby do oka tučňáka. V obrázku se tučňák na rybu nebude dívat přímo shora, abychom si na rozhraní voda-led a voda-vzduch mohli znázornit, jak se paprsek světla láme. Do obrázku vyznačte, kde tučňák rybu uvidí (její zdánlivý obraz).
Formulujte Snellův zákon lomu pro obě rozhraní.
Nápověda 2
Zdánlivou hloubku, ve které se ryba nachází, určíme z vhodných pravoúhlých trojúhelníků, které si do obrázku dokreslíme. Podobně jsme postupovali i v úloze Drozd a žížala, Řešení nápovědy 4, nyní máme ale situaci ztíženou tím, že nám do úlohy přibylo třetí optické rozhraní - led.
Nejprve si z obrázku vyjádřete \(\mathrm{tg}\,{α}\), \(\mathrm{tg}\,{β}\) a \(\mathrm{tg}\,{γ}\). Vztah pro \(\mathrm{tg}\,{α}\) zapište dvěma způsoby.
Nápověda 3
Využijeme paraxiální aproximace.
Nápověda 4
Nyní jsme si již odvodili všechny potřebné vztahy. Určete z těchto vztahů hloubku \(x\), ve které tučňák uvidí rybu.
Celkové řešení
Zákon lomu
Nakreslíme obrázek ukazující, jak paprsek dopadá od ryby do oka tučňáka. V obrázku se tučňák na rybu nebude dívat přímo shora, abychom si na rozhraní voda-led a voda-vzduch mohli znázornit, jak se paprsek světla láme.Paprsek dopadá od ryby na vrstvu ledu pod úhlem \(γ\), kde se láme a dopadá na hladinu vody pod úhlem \(β\), zde se opět láme a dopadá do oka tučňáka pod úhlem \(α\). Tento paprsek se řídí zákonem lomu. Protažením paprsku, který dopadá do oka tučňáka, můžeme zakreslit zdánlivý obraz ryby nacházející se v hloubce \(x\).
Napíšeme Snellův zákon lomu pro rozhraní vzduch-led: \[n_{1}\sin α=n_{2}\sin β,\tag{1}\] kde \( n_{1}\) je index lomu vzduchu a \(n_{2}\) je index lomu ledu.
Analogicky pro rozhraní led-voda bude platit: \[n_{2}\sin β=n_{3}\sin γ,\tag{2}\] kde \(n_{3}\) je index lomu vody.
Porovnáním předchozích dvou vztahů dostáváme: \[n_{1}\sin α=n_{3}\sin γ.\tag{3}\]
Díky paraxiální aproximaci (viz nápověda 3) můžeme v našem případě Snellův zákon lomu vyjádřit pomocí funkce tangens. To pro nás bude velmi užitečné, neboť tangenty úhlů \(α\), \(β\), \(γ\) si můžeme lépe vyjádřit z obrázku.
Přepíšeme si vztahy (1) a (3) dle paraxiální aproximace: \[n_{1}\mathrm{tg}\, α=n_{2}\mathrm{tg}\, β,\tag{11}\] \[n_{1}\mathrm{tg}\, α=n_{3}\mathrm{tg}\, γ.\tag{12}\] (Vztah (2) jsme nepřepisovali, protože ho v následujícím výpočtu nevyužijeme.)
Vyjádření \(\mathrm{tg}\,{α}\), \(\mathrm{tg}\,{β}\) a \(\mathrm{tg}\,{γ}\)
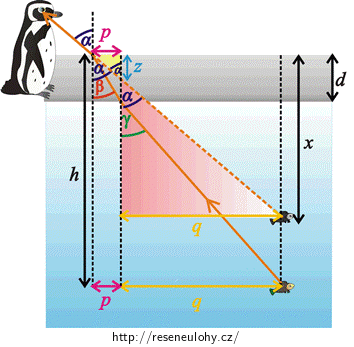
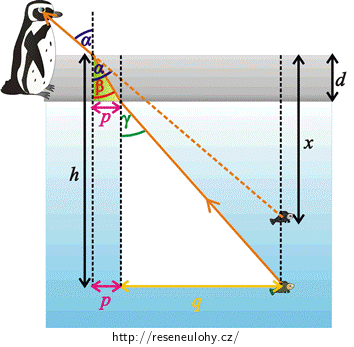
Do obrázku „Pozorování ryby“ si dokreslíme vhodné pravoúhlé trojúhelníky.
V obrázcích si zavedeme následující pomocné značení:
\(p\) je vzdálenost mezi kolmicí dopadu pro rozhraní vzduch-led a kolmicí dopadu pro rozhraní led-voda.
\(q\) je vzdálenost mezi kolmicí dopadu pro rozhraní led-voda a kolmým průmětem ryby na hladinu.
\(z\) je vzdálenost od hladiny k průsečíku kolmice dopadu pro rozhraní led-voda a pomyslného paprsku, který vede ke zdánlivému obrazu ryby.
Ze žlutého trojúhelníku vidíme, že: \[\mathrm{tg}\, {α}=\frac{p}{z}. \tag{4}\] Z červeného trojúhelníku můžeme odvodit: \[\mathrm{tg}\, {α}=\frac{q}{x−z}. \tag{5}\] Ze zeleného trojúhelníku vidíme, že bude platit: \[\mathrm{tg}\, {β}=\frac{p}{d}. \tag{6}\] Dle bílého trojúhelníku můžeme napsat: \[\mathrm{tg}\, {γ}=\frac{q}{h−d}. \tag{7}\] Vyjádření hledané hloubky \(x\)
Nejprve využijeme vztahu (11). Podíváme-li se na naše vztahy, vidíme, že když do vztahu (11) dosadíme vztahy (4) a (6), tak po úpravě ze vztahu zmizí \(p\) a můžeme vyjádřit \(z\): \[n_{1}\mathrm{tg}\, α=n_{2}\mathrm{tg}\, β,\] \[n_{1}\frac{p}{z}=n_{2}\frac{p}{d}.\] Obě strany rovnice vydělíme \(p\): \[n_{1}\frac{1}{z}=n_{2}\frac{1}{d}.\] Obě strany rovnice vynásobíme výrazem \(\frac{z}{n_{2}}d\): \[\frac{n_{1}}{n_{2}}d=z.\] Prohodíme levou a pravou stranu rovnice: \[z=d\frac{n_{1}}{n_{2}}.\tag{13}\]
Můžeme si všimnout, že teď by bylo užitečné použít vztah (12) a dosadit do něj (5) a (7): \[n_{1}\mathrm{tg}\, α=n_{3}\mathrm{tg}\, γ,\] \[n_{1}\frac{q}{x−z}=n_{3}\frac{q}{h−d}.\] \(q\) je na obou stranách, takže se vykrátí a v rovnici nám zbydou jen dvě neznámé (hledané \(x\) a \(z\), které už máme vyjádřené): \[n_{1}\frac{1}{x−z}=n_{3}\frac{1}{h−d}.\] Nyní chceme vyjádřit hloubku \(x\). Obě strany rovnice vynásobíme výrazem \(\left(x−z\right)\left(h−d\right)\): \[n_{1}\left(h−d\right)=n_{3}\left(x−z\right).\] Roznásobíme závorku na pravé straně rovnice: \[n_{1}\left(h−d\right)=n_{3}x−n_{3}z.\] K oběma stranám rovnice přičteme výraz \(n_{3}z\): \[n_{1}\left(h−d\right)+n_{3}z=n_{3}x.\] Obě strany rovnice vydělíme \(n_{3}\): \[\frac{n_{1}}{n_{3}}\left(h−d\right)+z=x.\] Prohodíme pravou a levou stranu rovnice a dosadíme za \(z\) dle (13): \[x=\frac{n_{1}}{n_{3}}\left(h−d\right)+\frac{n_{1}}{n_{2}}d.\]
Číselné řešení
Ze zadání víme:
\(h=2 \mathrm{m}\)
\(d=0{,}4 \mathrm{m}\)
V tabulkách dohledáme hodnotu indexu lomu vzduchu \(n_{1}\), ledu \(n_{2}\) a vody \(n_{3}\) :
\(n_{1}\) \(=\) \(1{,}00\)
\(n_{2}\) \(=\) \(1{,}31\)
\(n_{3}\) \(=\) \(1{,}33\)
Dosadíme:
\(x=\frac{n_{1}}{n_{3}}\left(h−d\right)+\frac{n_{1}}{n_{2}}d=\frac{1{,}00}{1{,}33}\left(2−0{,}4\right)+\frac{1{,}00}{1{,}31}\cdot 0{,}4 \mathrm{m} \dot= 1{,}51 \mathrm{m}.\)
Odpověď
Tučňák uvidí rybu v hloubce \(1{,}51 \mathrm{m}\).