Pozorování ryby přes spojnou čočku
Úloha číslo: 1857
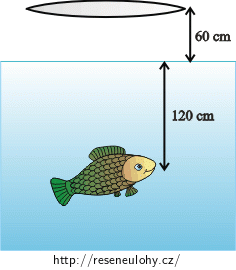
Malá rybka pluje \(120 \mathrm{cm}\) pod hladinou vody. Pozorujeme ji shora skrz tenkou spojnou čočku, která se nachází \(60 \mathrm{cm}\) nad hladinou vody. Ohnisková vzdálenost čočky je \(9 \mathrm{m}\) . V jaké hloubce uvidíme rybu?
Zápis
\(h=120 \mathrm{cm}= 1{,}2 \mathrm{m}\) hloubka, ve které plave ryba \(v=60 \mathrm{cm}= 0{,}6 \mathrm{m}\) výška nad hladinou, ve které se nachází spojná čočka \(f= 9 \mathrm{m}\) ohnisková vzdálenost čočky \(x= ?\) hloubka, ve které pozorovatel uvidí rybu skrz spojnou čočku Rozbor
V této úloze je naším cílem najít obraz, který vznikne po zobrazení ryby čočkou. Protože je čočka umístěna v jiném optickém prostředí než ryba, nebude předmětem pro zobrazování čočkou samotná ryba, ale její obraz, který bychom viděli pouhým okem. Z toho důvodu nejprve pomocí zákona lomu zjistíme, v jaké hloubce bychom viděli rybu bez použití čočky. Následně využijeme znalost zobrazovací rovnice čočky a určíme hloubku, ve které pozorujeme rybu přes tenkou spojnou čočku.
Nápověda 1
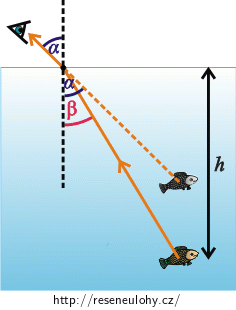
Nejprve určíme, v jaké hloubce bychom viděli rybu pouhým okem (bez spojky). Nakreslete obrázek ukazující, jak paprsek dopadá od ryby do oka pozorovatele. Na rybu se nebudeme dívat přímo shora, abychom si na rozhraní voda-vzduch mohli znázornit, jak se paprsek světla láme. Do obrázku vyznačte, kde pozorovatel rybu uvidí (její zdánlivý obraz). Formulujte Snellův zákon lomu.
Nápověda 2
Uvědomte si nebo vyhledejte, co je to tzv. paraxiální aproximace.
Nápověda 3
Nyní si do obrázku vyznačíme hloubku, ve které pozorovatel uvidí rybu pouhým okem. Užitím pravoúhlých trojúhelníků v obrázku a goniometrických funkcí tuto hloubku vypočítáme.
Nápověda 4
Už víme, jak polohu obrazu ryby zkresluje samotná voda. Proto se nyní můžeme podívat na rybu skrz čočku. Rozmyslete si, co budeme považovat za předmět, který bude čočka zobrazovat.
Nápověda 5
Využitím zobrazovací rovnice zjistěte, jaká je vzdálenost výsledného obrazu od středu čočky.
Nápověda 6
Zjistili jsme, že obrazová vzdálenost \(a'= −1{,}8 \mathrm{m}\). Co nám říká znaménko minus?
Určete, v jaké hloubce \(x\) uvidí pozorovatel rybu skrz spojku.
Celkové řešení
Hloubka, ve které pozorovatel uvidí rybu pouhým okem (bez spojky)
Nakreslíme si obrázek, ze kterého bude zřejmé, v jakém místě uvidí pozorovatel rybu pouhým okem. Na rybu se nebudeme dívat přímo shora, abychom si na rozhraní voda-vzduch mohli znázornit, jak se paprsek světla láme. Paprsek dopadá od ryby na hladinu vody pod úhlem \(β\), kde se láme a dopadá do oka pozorovatele pod úhlem \(α\). Tento paprsek se řídí zákonem lomu: \[n_{1}\sin α=n_{2}\sin β,\tag{1}\] kde \( n_{1}\) je index lomu vzduchu a \(n_{2}\) je index lomu vody.
Protažením paprsku, který dopadá do oka pozorovatele, můžeme zakreslit zdánlivý obraz ryby.
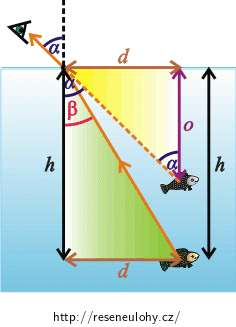
\(h\) je skutečná hloubka, ve které se ryba nachází; \(o\) značí hloubku, ve které pozorovatel uvidí rybu pouhým okem a \(d\) je vzdálenost mezi místem, kde se paprsek láme na hladině a kolmým průmětem ryby na hladinu.
Ze žlutého trojúhelníku určíme: \[\mathrm{tg}\, {α}=\frac{d}{o}. \tag{2}\] Ze zeleného trojúhelníku vidíme, že bude platit: \[\mathrm{tg}\, {β}=\frac{d}{h}. \tag{3}\]
Protože úhly \(α\), \(β\) jsou ve skutečnosti malé, bude platit (viz nápověda 2): \[\sin {α}=\mathrm{tg}\, {α},\tag{4}\] \[\sin {β}=\mathrm{tg}\, {β}.\tag{5}\]
Dosazením vztahu (2) do (4) a vztahu (3) do (5) dostáváme: \[\sin {α}=\frac{d}{o},\tag{6}\] \[\sin {β}=\frac{d}{h}.\tag{7}\] Vztahy (6), (7) dosadíme do rovnice pro zákon lomu (1): \[n_{1}\sin α=n_{2}\sin β,\tag{1}\] \[n_{1}\frac{d}{o}=n_{2}\frac{d}{h}.\] A vyjádříme si hloubku \(o\), ve které uvidíme obraz ryby: \[n_{1}\frac{1}{o}=n_{2}\frac{1}{h},\] \[\frac{1}{o}=\frac{n_{2}}{n_{1}h},\] \[o= h \frac{n_{1}}{n_{2}}.\tag{8}\]
Hloubka, ve které pozorovatel uvidí rybu skrz spojnou čočku
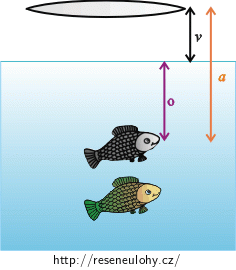
Pokud se na rybu budeme dívat přes spojnou čočku, musíme za předmět, který bude čočka zobrazovat, uvažovat obraz ryby, jehož polohu jsme si vyjádřili v předchozí části řešení. Předmětová vzdálenost \(a\) je vzdálenost od středu čočky k zobrazovanému předmětu. Zobrazovaným předmětem je obraz ryby v hloubce \(o\). \(v\) je vzdálenost spojky od hladiny vody.
Z obrázku vidíme, že platí: \[a=o+v.\tag{9}\]Napíšeme si zobrazovací rovnici: \[\frac{1}{f}=\frac{1}{a}+\frac{1}{a'},\] kde \(f\) je ohnisková vzdálenost čočky; \(a\), \(a'\) jsou předmětová a obrazová vzdálenost. Dosadíme za \(a\) dle (9): \[\frac{1}{f}=\frac{1}{o+v}+\frac{1}{a'}.\] A vyjádříme obrazovou vzdálenost \(a'\): \[\frac{1}{f}−\frac{1}{o+v}=\frac{1}{a'},\] \[\frac{o+v−f}{f\left(o+v\right)}=\frac{1}{a'},\] \[a'=\frac{f\left(o+v\right)}{o+v−f}.\tag{10}\]
Číselné řešení
Ze zadání víme:
\(v= 0{,}6 \mathrm{m}\)
\(f= 9 \mathrm{m}\)
\(h= 1{,}2 \mathrm{m}\)
V tabulkách dohledáme hodnotu indexu lomu vzduchu \(n_{1}\) a vody \(n_{2}\):
\(n_{1}\) \(=\) \(1{,}00\)
\(n_{2}\) \(=\) \(1{,}33\)
Dosazením do vztahu (8) určíme, v jaké hloubce \(o\) se nachází obraz ryby, pokud se na ni díváme bez čočky:
\(o=h \frac{n_{1}}{n_{2}}= 1{,}2 \frac{1{,}00}{1{,}33} \mathrm{m}= 0{,}9 \mathrm{m}.\)
Dosadíme do vztahu (10) a určíme vzdálenost výsledného obrazu ryby od čočky:
\(a'=\frac{f\left(o+v\right)}{o+v−f}= \frac{9\cdot\left(0{,}9+0{,}6\right)}{0{,}9+0{,}6−9} \mathrm{m}= \frac{13{,}5} {−7{,}5} \mathrm{m}= −1{,}8 \mathrm{m}.\)
Znaménko minus nám říká, že spojka vytvoří obraz na stejné straně čočky, na které je umístěn i zobrazovaný předmět.
Z pohledu pozorovatele bude tedy výsledný obraz ryby \(1{,}8 \mathrm{m} \) pod čočkou. Čočka se nachází ve výšce \(v= 0{,}6 \mathrm{m}\) nad hladinou vody. Z toho vyplývá, že pro hledanou hloubku platí \(x= 1{,}8 \mathrm{m} −0{,}6 \mathrm{m} = 1{,}2 \mathrm{m}= 120 \mathrm{cm}. \)
Odpověď
Rybu uvidíme \( 120 \mathrm{cm}\) pod hladinou, tedy v místě, kde se skutečně nachází.