Skleněná čočka s antireflexní vrstvou
Úloha číslo: 1616
Povrch skleněné čočky zhotovené ze skla o indexu lomu 1,8 je pokryt tenkou antireflexní vrstvou o indexu lomu 1,34. Na čočku dopadá kolmo bílé světlo. Určete nejmenší tloušťku tenké vrstvy pokrývající čočku, při které se maximálně zeslabí odražené světlo o vlnové délce 590 nm.
Nápověda 1
Připomeňte si, jak probíhá interference na tenké vrstvě. Pokud si nevíte rady, vyřešte si nejprve úlohu Vrstva oleje na vodě, kde je podrobné vysvětlení.
Nápověda 2
Jaké paprsky se spolu budou skládat a jaký bude celkový dráhový rozdíl těchto paprsků?
Zápis
ns = 1,8 relativní index lomu skla n = 1,34 relativní index lomu antireflexní vrstvy λ = 590 nm = 5,9·10−7 m vlnová délka dopadajícího světla d = ? (µm) tloušťka antireflexní vrstvy Řešení
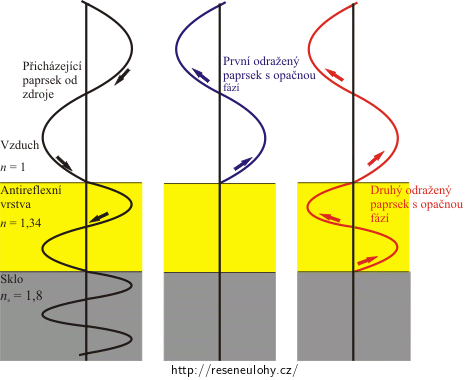
Paprsek přicházející od zdroje se částečně odrazí na rozhraní s antireflexní vrstvou a částečně projde do vrstvy. Při interferenci se složí paprsek, který se odrazil od antireflexní vrstvy, s paprskem, který prošel touto vrstvou a odrazil se na rozhraní se sklem. V obou případech se paprsky odráží na opticky hustším prostředí a oba se odrazí s opačnou fází. Protože ke změně fáze dojde u obou paprsků, neprojeví se v jejich vzájemném dráhovém rozdílu a nemusíme je nadále uvažovat. Pro nás je důležité, že druhý paprsek musí urazit kus dráhy navíc v porovnání s prvním, a to:
\[\mathrm{\Delta}l =\, \mathrm{2}nd,\]kde n je index lomu antireflexní vrstvy a d je tloušťka antireflexní vrstvy.
Jelikož potřebujeme, aby se paprsky zeslabily, tedy aby vzniklo interferenční minimum, musí se celkový dráhový rozdíl paprsků Δl rovnat lichému násobku poloviny vlnové délky:
\[\mathrm{\Delta}l =\,(2k + 1)\frac{\lambda}{2}.\]Pro nalezení nejtenčí vrstvy dosadíme za k = 0. Nyní rovnice dosadíme jednu do druhé a vyjádříme d:
\[\frac{\lambda}{2}=\,\mathrm{2}nd \quad\Rightarrow\quad d=\,\frac{\lambda}{\mathrm{4}n}.\]Dosadíme hodnoty ze zadaní a získáme hledané d:
\[d=\,\frac{5{,}9{\cdot}10^{−7}}{4\,\cdot\,1{,}34}\,\mathrm{m}=\,1{,}1{\cdot}10^{−7}\,\mathrm{m}=\,0{,}11\,\mathrm{µm}.\]Odpověď
Tloušťka antireflexní vrstvy, která pokrývá čočku, je 0,11 µm.
Komentář – význam antireflexní vrstvy
Někdy potřebujeme, aby odrazivost materiálu byla malá, v jiných případech je lepší velká. U fotoaparátu je výhodné odrazivost snižovat, aby většina světla prošla čočkami fotoaparátu a fotka byla správně osvětlená. Někdy se však snažíme odrazivost zvýšit. Například na bižuterii se nanáší materiály s větším indexem lomu, aby se určité vlnové délky zesílily a šperky získaly barevné odlesky.
Komentář – dodatek k řešení
V předchozím řešení jsme nebrali v úvahu odraz obou paprsků s opačnou fází. Řekli jsme, že se vyruší a tedy není nutné s nimi počítat.
Teď ovšem s nimi počítat budeme. Napíšeme si dráhové rozdíly obou paprsků do detailu: první paprsek se odrazí s opačnou fází:
\[\mathrm{\Delta}l_\mathrm{1} =\ \frac{\lambda}{2},\]druhý paprsek se odrazí s opačnou fází a k tomu projde navíc optickou dráhu 2nd:
\[\mathrm{\Delta}l_\mathrm{2} =\ \frac{\lambda}{2}+ \mathrm{2}nd,\]takže dráhový rozdíl obou paprsků bude:
\[\mathrm{\Delta}l=\mathrm{\Delta}l_\mathrm{2} − \mathrm{\Delta}l_\mathrm{1} =\ \frac{\lambda}{2}+ \mathrm{2}nd − \frac{\lambda}{2} = \mathrm{2}nd.\]Po tomto kroku už je postup řešení stejný.