Sbírka řešených úloh

Jak vysoký je nejvyšší strom?

Úloha číslo: 1917

V Kalifornii nalezneme nejvyšší žijící strom na světě. Druh stromu se nazývá sekvoj vždyzelená a jméno tohoto stromu je Hyperion.

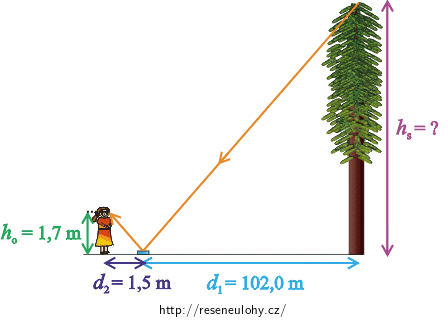
Přestavte si, že byste chtěli změřit jeho výšku. Do vzdálenosti \(102 \mathrm{m}\) od stromu položíte zrcátko. Postavíte-li se \(150 \mathrm{cm}\) od zrcátka (tedy \(103{,}5 \mathrm{m}\) od stromu), uvidíte v zrcátku špičku Hyperionu.

Dokážete nyní určit jakou výšku má tento strom?

Předpokládejte, že strom, pozorovatel i zrcátko se nachází na rovném terénu a oči pozorovatele jsou ve výšce \(170 \mathrm{cm}\) nad zemí.

 

Poznámka: Výška Hyperionu, kterou v této úloze vypočítáme, byla změřena v roce 2010.

• Zápis

  \(d_{1}=102{,}0 \mathrm{m}\)	vzdálenost mezi stromem a zrcátkem
  \(d_{2}=150 \mathrm{cm}=1{,}5 \mathrm{m}\)	vzdálenost mezi pozorovatelem a zrcátkem
  \(h_{o}=170 \mathrm{cm}=1{,}7 \mathrm{m}\)	výška, ve které se nachází oči pozorovatele
  \(h_{s}= ?\)	výška stromu Hyperion

• Nápověda 1

  Nakreslete, jak bude vypadat situace při měření výšky stromu, a obrázek popište.

• Řešení nápovědy 1

  Kreslíme obrázek dle zadání. Chceme, aby pozorovatel viděl v zrcadle špičku stromu, proto musí paprsek dopadající od špičky stromu dopadnout na zrcadlo a po odrazu dopadnout do očí pozorovatele.

  

• Nápověda 2

  Paprsek dopadající od špičky stromu do oka pozorovatele, splňuje zákon odrazu. Jak zní tento zákon a co z této informace vyplývá pro náš obrázek?

• Řešení nápovědy 2

  Zákon odrazu nám říká, že úhel dopadu \(α\) je stejný jako úhel odrazu. To zároveň znamená, že úhel který svírá dopadající paprsek s vodorovnou rovinou je stejný jako úhel, který svírá odražený paprsek s vodorovnou rovinou (\(90°−α\)).

  

  V obrázku se nachází dva trojúhelníky (označíme je zeleně a žlutě), o kterých víme, že mají jeden úhel (označený růžově) stejný.

  

  Dále si uvědomíme, že žena i strom svírají s vodorovnou rovinou pravý úhel. Zelený a žlutý trojúhelník mají tedy dva shodné úhly. Pokud se dva trojúhelníky shodují ve dvou úhlech, pak jsou tyto trojúhelníky podobné.

• Nápověda 3

  Nyní víme, že trojúhelníky z obrázku (viz řešení nápovědy 2) jsou podobné. Zamyslete se, zda této informace nemůžete nějakým způsobem využít při hledání výšky stromu.

• Řešení nápovědy 3

  

  Pro podobné trojúhelníky platí, že se poměry odpovídajících si stran shodují:

  \[\frac{h_{s}}{h_{o}}=\frac{d_{1}}{d_{2}}.\]

  Abychom získali vztah pro výpočet výšky stromu, obě strany rovnice vynásobíme \(h_{o}\):

  \[h_{s}=h_{o}\frac{d_{1}}{d_{2}}.\]

   

  Číselné řešení

  Ze zadání víme:

  \(h_{o}=170 \mathrm{cm}=1{,}7 \mathrm{m}\)

  \(d_{1}=102{,}0 \mathrm{m}\)

  \(d_{2}=150 \mathrm{cm}=1{,}5 \mathrm{m}\)

  Dosadíme:

  \(h_{s}=h_{o}\frac{d_{1}}{d_{2}}=1{,}7\cdot \frac{102{,}0}{1{,}5} \mathrm{m}=115{,}6 \mathrm{m}.\)

• Celkové řešení

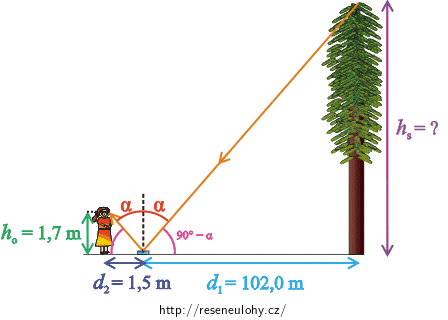
  Nejprve si nakreslíme obrázek. Chceme, aby pozorovatel viděl v zrcadle špičku stromu. Proto musí paprsek jdoucí od špičky stromu dopadnout na zrcadlo a po odrazu dopadnout do očí pozorovatele. Tento paprsek splňuje zákon odrazu.

  

  Zákon odrazu nám říká, že úhel dopadu \(α\) je stejný jako úhel odrazu. To zároveň znamená, že úhel který svírá dopadající paprsek s vodorovnou rovinou je stejný jako úhel, který svírá odražený paprsek s vodorovnou rovinou (\(90°−α\)).

   

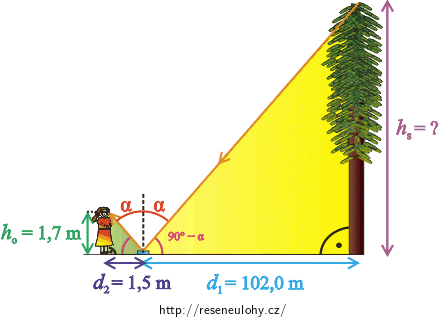
  Nyní se podíváme na dva trojúhelníky, které nám v obrázku vznikly (jsou označeny zeleně a žlutě).

  

  Již víme, že tyto trojúhelníky mají jeden úhel (označený růžově) stejný. Zároveň jsou oba trojúhelníky pravoúhlé. Zjistili jsme tedy, že se trojúhelníky shodují ve dvou úhlech, a to znamená, že se jedná o trojúhelníky podobné.

   

  Pro podobné trojúhelníky platí, že se poměry odpovídajících si stran shodují:

  \[\frac{h_{s}}{h_{o}}=\frac{d_{1}}{d_{2}}.\]

  Obě strany rovnice vynásobíme \(h_{o}\) a získáme tak hledaný vztah pro výpočet výšky stromu:

  \[h_{s}=h_{o}\frac{d_{1}}{d_{2}}.\]

   

  Číselné řešení

  Ze zadání víme:

  \(h_{o}=170 \mathrm{cm}=1{,}7 \mathrm{m}\)

  \(d_{1}=102{,}0 \mathrm{m}\)

  \(d_{2}=150 \mathrm{cm}=1{,}5 \mathrm{m}\)

  Dosadíme:

  \(h_{s}=h_{o}\frac{d_{1}}{d_{2}}=1{,}7\cdot \frac{102{,}0}{1{,}5} \mathrm{m}=115{,}6 \mathrm{m}.\)

• Odpověď

  Výška Hyperionu je \(115{,}6 \mathrm{m}\).