Sbírka řešených úloh

Výpočet Brewsterova úhlu z mezního úhlu

Úloha číslo: 1645

• Nápověda 1

  Co je to mezní úhel?

• Řešení nápovědy 1

  Mějme optické rozhraní sklo – vzduch. Světlo, které bude dopadat na optické rozhraní, se bude odrážet a lámat. Pokud budeme zvětšovat úhel dopadu, bude růst i úhel lomu, až dosáhneme takového úhlu dopadu, kdy se bude paprsek lámat pod úhlem 90°. Tento úhel nazveme mezní úhel α_m. Pro úhly dopadu větší než α_m už nedochází k žádnému lomu a veškeré světlo se odráží, vzniká tzv. totální odraz.

  

  K totálnímu odrazu dochází jen v případě, že světlo dopadá na rozhraní z opticky hustšího materiálu na materiál opticky řidší, protože potom je úhel lomu větší než úhel dopadu (tzv. lom od kolmice).

• Nápověda 2

  Jak pomocí mezního úhlu můžeme spočítat index lomu použitého skla?

• Řešení nápovědy 2

  

  Pro výpočet indexu lomu použitého skla využijeme Snellův zákon:

  \[n_\mathrm{1} \sin \alpha_\mathrm{m} = \, n_\mathrm{2} \sin \beta \quad\Rightarrow\quad n_\mathrm{1} \sin \alpha_\mathrm{m} = \, \sin 90°,\]

  kde n₁ je index lomu skla, α_m je mezní úhel, n₂ = 1 je index lomu vzduchu a β je úhel lomu. Z tohoto vztahu si vyjádříme index lomu skla n₁.

• Nápověda 3

  Brewsterův úhel je úhel pro úplnou polarizaci odrazem. Připomeňte si, jaká podmínka platí pro tzv. Brewsterův úhel dopadu.

  Pokud si nevzpomínáte, podívejte se nejprve do řešení v úloze Polarizace úplným odrazem.

• Nápověda 4

  Jak můžeme spočítat Brewsterův úhel s použitím vypočítaného indexu lomu skla, pro odraz světla přicházejicího a) zvenčí a b) zevnitř skla?

• Řešení nápovědy 4

  Brewsterův úhel je takový úhel dopadu, při kterém odražený a lomený paprsek svírají pravý úhel.

  a) Odraz světla přicházejícího zvenčí

   

  

  Z obrázku získáme vztah:

  \[\alpha_\mathrm{B}+ 90° + \beta = 180° \quad\Rightarrow\quad \beta = 90° − \alpha_\mathrm{B}. \]

  Potom lze upravit Snellův zákon a dosadit za β:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\, \beta}=\,\frac{n_\mathrm{1}}{n_\mathrm{2}} \quad\Rightarrow\quad \frac{\sin\, \alpha_\mathrm{B}}{\sin\,(90° − \alpha_\mathrm{B})}=\,\frac{n_\mathrm{1}}{1}.\]

  S využitím vlastností goniometrických funkcí sin(90° − α) = cos α, lze předchozí vztah přepsat na:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\,\mathrm{tg}\,\, \alpha_\mathrm{B}=\,n_\mathrm{1},\]

  kde α_B je Brewsterův úhel dopadu a n₁ je index lomu skla. Nyní už jen dosadíme hodnoty a provedeme výpočet.

   

  b) Odraz světla přicházejícího zevnitř

  

  Při výpočtu budeme postupovat jako v první části řešení, jen ve Snellově zákonu se prohodí oba indexy lomu, tj. bude mít tvar:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\, \beta}=\,\frac{n_\mathrm{2}}{n_\mathrm{1}} \quad\Rightarrow\quad \frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\,\mathrm{tg}\,\, \alpha_\mathrm{B}=\,\frac{1}{n_\mathrm{1}}.\]

  Teď můžeme dosadit hodnoty a vypočítat Brewsterův úhel.

• Řešení

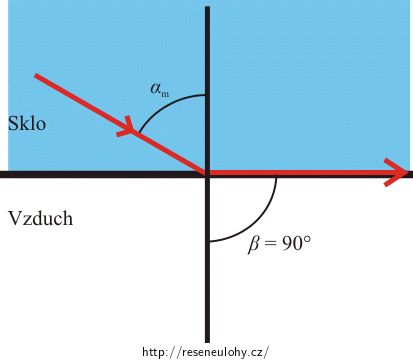
  Pokud při dopadu světla na optické rozhraní budeme zvětšovat úhel dopadu, bude růst i úhel lomu. Pokud dosáhneme takového úhlu dopadu, kdy se bude paprsek lámat pod úhlem 90°, takový úhel nazýváme mezní úhel α_m. Pro úhly dopadu větší než α_m nedochází k lomu a vše se odráží, tzv. totální odraz. K tomu může dojít, jen pokud světlo dopadá na rozhraní z opticky hustšího materiálu na materiál opticky řidší.

   

  Pro výpočet Brewsterova úhlu použitého skla potřebujeme nejdříve vypočítat jeho index lomu.

  

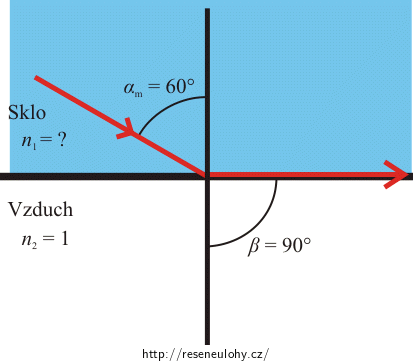
  Napíšeme si Snellův zákon ve tvaru:

  \[n_\mathrm{1} \sin \alpha_\mathrm{m} = \, n_\mathrm{2} \sin \beta \quad\Rightarrow\quad n_\mathrm{1} \sin \alpha_\mathrm{m} = \, \sin 90° = 1,\]

  kde n₁ je index lomu skla, α_m je mezní úhel, n₂ = 1 je index lomu vzduchu a β je úhel lomu.

  Z předchozího vztahu si vyjádříme index lomu skla n₁ a dosadíme hodnoty za β a α_m. Dostaneme:

  \[n_\mathrm{1}=\,\frac{1}{\sin \alpha_\mathrm{m}}.\]

  Tuto hodnotu indexu lomu skla použijeme v dalších výpočtech pro Brewsterův úhel, tedy úhel dopadu, při kterém odražený a lomený paprsek svírají pravý úhel.

   

  a) Odraz světla přicházejícího zvenčí

  Pro výpočet získáme vztah:

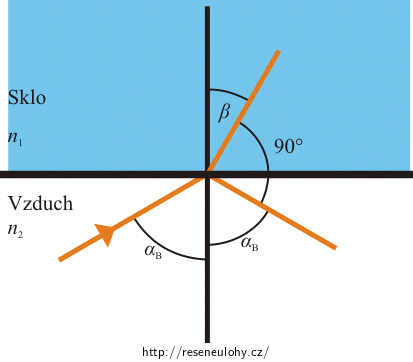
  \[\alpha_\mathrm{B}+ 90° + \beta = 180° \quad\Rightarrow\quad \beta= 90° − \alpha_\mathrm{B}. \]

  Potom lze upravit Snellův zákon a dosadit za β:

  \[\frac{\sin\, \alpha_\mathrm{B}}{\sin\, \beta}=\, \frac{\sin\, \alpha_\mathrm{B}}{\sin\,(90° − \alpha_\mathrm{B})}=\frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\,\mathrm{tg}\,\, \alpha_\mathrm{B}=\,\frac{n_\mathrm{1}}{n_\mathrm{2}}= \,n_\mathrm{1},\]

  kde α_B je Brewsterův úhel dopadu, n₁ je index lomu skla a n₂ = 1 je index lomu vzduchu. Nyní dosadíme a získáme Brewsterův úhel dopadu pro odraz světla zvenčí.

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}=\,n_\mathrm{1}=\,\frac{1}{\sin \alpha_\mathrm{m}}=\,\frac{1}{\sin 60°},\]

  tedy

  \[\alpha_\mathrm{B}\dot=\, 49°.\]

   

  b) Odraz světla přicházejícího zevnitř

  Při výpočtu budeme postupovat jako v první části řešení, jen ve Snellově zákoně se prohodí oba indexy lomu:

  \[\frac{\sin\,\alpha_\mathrm{B}}{\sin\, \beta}=\,\frac{n_\mathrm{2}}{n_\mathrm{1}} \quad\Rightarrow\quad \frac{\sin\, \alpha_\mathrm{B}}{\cos\,\alpha_\mathrm{B}}=\,\mathrm{tg}\,\, \alpha_\mathrm{B}=\,\frac{1}{n_\mathrm{1}}.\]

  Dosadíme a získáme Brewsterův úhel dopadu pro odraz světla zevnitř.

  \[\mathrm{tg}\,\, \alpha_\mathrm{B}=\,\frac{1}{\frac{1}{\sin \alpha_\mathrm{m}}}=\,\sin \alpha_\mathrm{m}=\,\sin 60°,\]

  tedy

  \[\alpha_\mathrm{B}\dot=\, 41°.\]

• Odpověď

  Velikost Brewsterova úhlu pro odraz světla zvenčí je 49° a pro odraz světla zevnitř je 41°.