Youngův interferenční pokus (nestejně široké štěrbiny)

Úloha číslo: 1559

Vypočtěte relativní osvětlení na stínítku pro Youngův interferenční pokus za podmínky, že obě štěrbiny jsou velmi úzké, avšak poměr jejich šířek \(p\) nemusí být \(1\). Vzdálenost štěrbin je \(d\), na rovinu štěrbin dopadá kolmo rovinná monochromatická harmonická vlna.

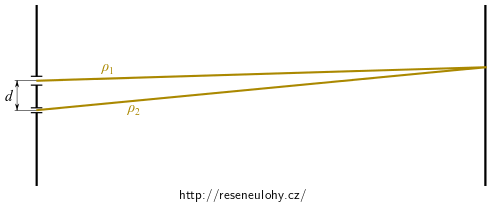
Porovnejte průběhy intenzit pro případy \(p=1\) a \(p\neq1\).

Odkaz na podobné úlohy
Před řešením této úlohy doporučujeme prostudovat úlohu Youngův pokus, která je její jednodušší variantou.

Dále lze také řešit složitější úlohy Ohyb na dvojité štěrbině a Ohyb na dvojité štěrbině alternativně, kde se již štěrbiny nepovažují za velmi úzké (centrální ohybové maximum bude užší) a do interferenčního obrazce „zasáhne“ ohybový průběh.
Rozbor
• Při výpočtu budeme používat komplexní formalismus, s nímž jsme se seznámili zde a pracovali jsme s ním v této úloze.

• V Youngově pokusu jde o tzv. Fraunhoferův ohyb, tj. interferenční obrazec zkoumáme na velmi vzdáleném stínítku. Právě díky této podmínce lze při výpočtu přistoupit k řadě zjednodušení.

• Štěrbiny jsou velmi úzké, budeme tedy předpokládat, že při osvětlení jen jedné štěrbiny by díky ohybu na ní bylo osvětlení stínítka rovnoměrné. Na štěrbiny tedy budeme nahlížet jako na přímkové zdroje válcových vln. Konkrétní funkci popisující šíření elektrické intenzity odvodíme později.

• Nestejná šířka štěrbin se projeví v rozdílné intenzitě světla jimi procházivší. Naším úkolem je zjistit, jak se různost šířek štěrbin projeví na interferenčním obrazci.

• Intenzita světla je úměrná střední hodnotě druhé mocniny elektrické intenzity, v komplexním formalismu \[ I \sim EE^\star , \] kde hvězdička značí komplexní sdružení.

• Pro malé úhly \(\delta \ll 1\) je \[ \sin\delta \,\approx\, \tan \delta . \]
Postup řešení
Nejprve nalezneme funkci vyjadřující závislost elektrické intenzity na čase, vzdálenosti a šířce jedné štěrbiny. Dále určíme příspěvky elektrické intenzity od obou štěrbin v daném místě stínítka. Jejich součet bude představovat výslednou elektrickou intenzitu. Nalezneme závislost na úhlu \(\theta\). Relativní osvětlení pak získáme součinem výsledné elektrické intenzity s jejím komplexním sdružením.

Tento postup je přímým důsledkem skutečností diskutovaných v rozboru.
Nápověda 1 – průběh el. intenzity od jedné štěrbiny
Nejprve nalezněte funkci vyjadřující závislost elektrické intenzity na čase, vzdálenosti a šířce štěrbiny. Uvědomte si, že jde o válcovou vlnu, jejíž amplituda klesá se vzdáleností a je závislá na šířce štěrbiny.
Řešení nápovědy 1 – průběh el. intenzity od jedné štěrbiny

Jde o válcovou (harmonickou, monochromatickou) vlnu, tj. v místech vzdálených od štěrbiny \(\rho\) bude stejná elektrická intenzita a amplituda bude klesat s \(\sqrt{\rho}\) ^[Proč?]
\[E(\rho,t) \sim \frac{1}{\sqrt{\rho}} e^{i(\omega t - k\rho)}.\tag{1}\]
Dále musíme zohlednit to, že intenzita světla \(I\) na stínítku je přímo úměrná šířce štěrbiny \(b\) – např. dvakrát větší štěrbina znamená, že za daný čas dopadne na stejnou plochu stínítka dvakrát více energie (místo štěrbiny si můžete představit zářivku, akt zdvojnásobení pak představuje přidání druhé zářivky). Jak bude na šířce štěrbiny \(b\) záviset elektrická intenzita \(E\)? Intenzita \(I\) je úměrná součinu \(EE^\star\), tj. v reálné reprezentaci \(E^2\). Rekapitulace a závěr z tohoto odstavce:
\[ \left. \begin{array}{ll} \circ\quad\text{Intenzita přímo úměrná šířce štěrbiny:} & I \sim b\\ \circ\quad\text{Intenzita úměrná dvojmoci el. intenzity:} & I \sim E^2 \end{array} \quad\right\}\ \Rightarrow\quad E^2 \sim b \quad \Rightarrow \quad E \sim \sqrt{b}. \]
Elektrická intenzita je tedy úměrná odmocnině šířky štěrbiny
\[E(b) \sim \sqrt{b}.\tag{2}\]
Uvážením závislostí (1) a (2) a přidáním konstanty úměrnosti \(\mathcal{E}\), jejíž velikost souvisí s intenzitou na štěrbiny dopadající rovinné vlny, máme funkci
\[ E(t,\rho,b) = \mathcal{E} \sqrt{\frac{b}{\rho}} \, e^{i(\omega t - k\rho)}, \tag{3}\]
vyjadřující velikost elektrické intenzity v čase \(t\) ve vzdálenosti \(\rho\) od štěrbiny, jejíž šířka je \(b\).
Nápověda 2 – superpozice vln na stínítku
Na základě nalezeného vyjádření (3) pro závislost \(E(\rho, b, t)\) zapište příspěvky elektrických intenzit v daném místě stínítka od obou štěrbin. Tyto příspěvky superponujte a výraz pro výslednou intenzitu zjednodušte přihlédnutím ke skutečnosti, že jde o Fraunhoferův ohyb. Poměr šířek štěrbin je \(p\).

Aby bylo možné velikosti elektrických intenzit přímo sčítat, musí mít vektory elektrické intenzity válcových vln z obou štěrbin v uvažovaném místě stínítka stejný směr. To je přibližně splněno, neboť při velmi vzdáleném a dostatečně malém stínítku jsou průvodiče od obou štěrbin téměř rovnoběžné. Alternativně lze požadovat, aby dopadající vlna byla lineárně polarizovaná ve směru štěrbin.
Řešení nápovědy 2 – superpozice vln na stínítku
Uvažujme místo na stínítku, které je od první štěrbiny šířky \(b_1\) vzdálené \(\rho_1\) a od druhé štěrbiny šířky \(b_2\) vzdálené \(\rho_2\). Elektrické intenzity válcových vln od první a druhé štěrbiny jsou
\[ \begin{eqnarray} E_1 &=& \mathcal{E} \sqrt{\frac{b_1}{\rho_1}} \, e^{i(\omega t - k\rho_1)},\\ E_2 &=& \mathcal{E} \sqrt{\frac{b_2}{\rho_2}} \, e^{i(\omega t - k\rho_2)}. \end{eqnarray} \]
Tyto příspěvky na stínítku superponují. Předpokládáme-li, že vektory elektrických intenzit obou vln mají přibližně stejný směr, je výsledná intenzita součtem přímo velikostí \(E_1, E_2\)
\[ E = E_1 + E_2 = \mathcal{E} \left( \sqrt{\frac{b_1}{\rho_1}} \, e^{i(\omega t - k\rho_1)} + \sqrt{\frac{b_2}{\rho_2}} \, e^{i(\omega t - k\rho_2)} \right)= \]
protože je stínítko velmi daleko, je \(\rho_1 \approx \rho_2 \approx l\), kde \(l\) je vzdálenost stínítka a štěrbin, a proto
\[ =\mathcal{E}\frac{1}{\sqrt{l}} \left( \sqrt{b_1} \, e^{i(\omega t - k\rho_1)} + \sqrt{b_2} \, e^{i(\omega t - k\rho_2)} \right)= \]
dále vytkneme i \(\sqrt{b_1}\)
\[ =\mathcal{E}\sqrt{\frac{b_1}{l}} \bigg( e^{i(\omega t - k\rho_1)} + \underbrace{\sqrt{\frac{b_2}{b_1}}}_{\sqrt{p}} \, e^{i(\omega t - k\rho_2)} \bigg)= \]
a ve zbylém výrazu identifikujeme poměr šířek štěrbin \(\frac{b_2}{b_1} = p\). Máme tak
\[ E = \mathcal{E}\sqrt{\frac{b_1}{l}} \left( e^{i(\omega t - k\rho_1)} + \sqrt{p} e^{i(\omega t - k\rho_2)} \right). \tag{4}\]
Nápověda 3 – závislost na θ
Našli jsme vztah (4) pro elektrickou intenzitu na stínítku, který je ale funkcí vzdáleností \(\rho_1\), \(\rho_2\) od štěrbin. Upravte vztah tak, aby v něm figuroval rozdíl těchto vzdáleností a posléze i úhel \(\theta\), který vyjadřuje úhel odklonu daného místa od normály roviny štěrbin.
Řešení nápovědy 3 – závislost na θ
Do výrazu pro intenzitu
\[E = \mathcal{E}\sqrt{\frac{b_1}{l}} \left( e^{i(\omega t - k\rho_1)} + \sqrt{p} e^{i(\omega t - k\rho_2)} \right)= \]
se budeme nejprve snažit dostat rozdíl vzdáleností \(\rho_1\), \(\rho_2\). Vytkněme ze závorky první člen dvojčlenu
\[ = \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{i(\omega t - k\rho_2)} e^{-i(\omega t - k\rho_1)} \right) = \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{ik(\rho_1 - \rho_2)} \right). \]
V závorce konečně dostáváme dráhový rozdíl \(\Delta\rho = \rho_1 - \rho_2\).
\[ E= \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{ik\Delta \rho} \right). \]
Je-li stínítko velmi daleko od dvojštěrbiny a jsou-li štěrbiny dostatečně blízko, je směr průvodičů \(\rho_1\), \(\rho_2\) téměř rovnoběžný s jejich osou.

Dráhový rozdíl \(\Delta\rho\) je nejkratší strana v naznačeném zeleném trojúhelníku. Na obrázku vpravo je zvětšený.

Trojúhelník je v této aproximaci téměř pravoúhlý, proto
\[ \Delta \rho = d \sin \theta. \]
kde úhel \(\theta\) je současně odchylkou osy interferujících paprsků od normály stínítka.

Elektrická intenzita v místě stínítka určeném úhlem \(\theta\) je proto
\[ E= \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{ikd\sin\theta} \right). \tag{5}\]
Nápověda 4 – výpočet relativní intenzity světla na stínítku
Určete průběh relativní intenzity světla na stínítku. Užijte odvozeného vyjádření (5) pro \(\vec{E}\).

Intenzita světla je úměrná výrazu \(EE^\star\), viz rozbor.
Řešení nápovědy 4 – výpočet intenzity světla na stínítku
Určíme relativní průběh intenzity světla na stínítku dosazením vyjádření (5) do obecného vztahu
\[ I \sim EE^\star = \mathcal{E}^2 \frac{b_1}{l} \underbrace{e^{i(\omega t - k\rho_1)}e^{-i(\omega t - k\rho_1)}}_{1} \left( 1 + \sqrt{p} e^{ikd\sin\theta} \right) \left( 1 + \sqrt{p} e^{-ikd\sin\theta} \right)= \] \[ = \mathcal{E}^2 \frac{b_1}{l} \left( 1 + \sqrt{p}e^{-ikd\sin\theta} + \sqrt{p}e^{ikd\sin\theta} + p \underbrace{e^{ikd\sin\theta} e^{-ikd\sin\theta} }_{1} \right) = \] \[ = \mathcal{E}^2 \frac{b_1}{l} \left[ 1 + p + \sqrt{p}\left( e^{ikd\sin\theta} + e^{-ikd\sin\theta} \right)\right]. \]
Výraz v kulaté závorce upravíme zvlášť.

Rozepsáním komplexních exponenciál z Eulerova vztahu \(\color{MidnightBlue}{e^{i\varphi} = \cos\varphi + i\sin\varphi}\) a úpravou
\[ e^{ikd\sin\theta} + e^{-ikd\sin\theta} = \] \[ \color{MidnightBlue}{ = \cos (kd\sin\theta) + i \sin (kd\sin\theta) + \cos (kd\sin\theta) - i \sin (kd\sin\theta) = } \] \[ \color{MidnightBlue}{ = 2\cos (kd\sin\theta). } \]

Dostáváme relativní závislost intenzity na úhlu \(\theta\)
\[ I(\theta) \sim \mathcal{E}^2 \frac{b_1}{l} \left[ 1 + p + 2\sqrt{p}\cos(kd\sin\theta) \right]. \tag{6}\]
Intenzita osvětlení stínítka je globálně úměrná dvojmoci osvětlení štěrbin (\(\mathcal{E}^2\)), přímo úměrná šířce štěrbin (\(b_1\)). Naopak čím dál bude stínítko, tím bude intenzita menší (\(1/l\)). Úhlovou závislost a souvislost s poměrem šířek štěrbin \(p\) podiskutujeme v dalším oddílu.
Nápověda 5 – relativní osvětlení a ohybový obrazec
Našim úkolem bylo nalézt funkci vyjadřující relativní osvětlení stínítka. Vyšetřete tuto funkci pro oba případy \(p=1\) a \(p \neq 1 \). Nakreslete grafy funkcí.
Řešení nápovědy 5 – relativní osvětlení a ohybový obrazec
Člen před závorkou je pro dané uspořádání experimentu konstantní
\[I(\theta) \sim \mathcal{E}^2\frac{b_1}{l} \left( 1 + p + 2\sqrt{p}\cos(kd\sin\theta) \right).\]
Relativní osvětlení stínítka tedy určuje funkce v závorce
\[ I_r(\theta) = 1 + p + 2\sqrt{p}\cos(kd\sin\theta) \]
Funkce \(I_r(\theta)\) nabývá
\[ \begin{array}{lllll} \circ\ \text{maxima} & \text{pro} & \cos(kd\sin\theta) = 1 & \text{tj. když} & kd\sin\theta = 2\pi m,~m\in\mathbb{Z}\\ \circ\ \text{minima} & \text{pro} & \cos(kd\sin\theta) = -1 & \text{tj. když} & kd\sin\theta = \pi + 2\pi m,~m\in\mathbb{Z} \end{array} \]
tj. polohy minim a maxim nezávisí na poměru \(p\), obrazec se se změnou \(p\) nikam „neposouvá“. Co se může měnit, je hodnota funkce, tj. intenzita.

Proveďme jednu „trikovou“ úpravu
\[ I_r(\theta) = 1 + p + 2\sqrt{p}\cos(kd\sin\theta) = 1 + p - \underbrace{2\sqrt{p} + 2\sqrt{p}}_{\text{odečtu a přičtu}} + 2\sqrt{p}\cos(kd\sin\theta) = \] \[ = 1 + p - 2\sqrt{p} + 2\sqrt{p}\left[1 + \cos(kd\sin\theta) \right] = 1 + p - 2\sqrt{p} + 4\sqrt{p}\frac{1 + \cos(kd\sin\theta) }{2} = \] \[ = \underbrace{1 + p - 2\sqrt{p}}_{\text{ozn. }I_\mathrm{min}} + 4\sqrt{p} \cos^2\left(\frac{kd\sin\theta}{2}\right). \]
V posledním kroku jsme použili goniometrický vztah \(\small \frac{1+\cos x}{2} = \cos^2 \frac{x}{2} \).

Máme tedy ohybovou funkci ve tvaru
\[ I_r(\theta) = I_\mathrm{min}(p) + 4\sqrt{p} \cos^2\left(\frac{kd\sin\theta}{2}\right), \] \[ \text{kde}\quad I_\mathrm{min}(p) = 1 + p - 2\sqrt{p}. \]
Funkce \(I_\mathrm{min}(p)\) je nulová pouze pro \(p=1\), tj. v případě stejně širokých štěrbin, kdy se jedná o standardní Youngův experiment, jehož ohybový obrazec má nulová minima.

Jestliže je \(p\neq 1\), pak je funkce \(I_\mathrm{min}\) kladná a ohybový obrazec je posunutý ve směru kladné osy y, tj. má nenulová minima. Viz následující obrázek.

Funkce \(I_\mathrm{min}\) je rostoucí, tj. se zvětšováním poměru štěrbin \(p\) se zvětšuje i minimální hodnota intenzity na stínítku a současně pro \(p\gt 1\) se zvětšuje i obor hodnot celé ohybové funkce, tj. v maximech je dosahováno vyšších hodnot.
CELKOVÉ ŘEŠENÍ

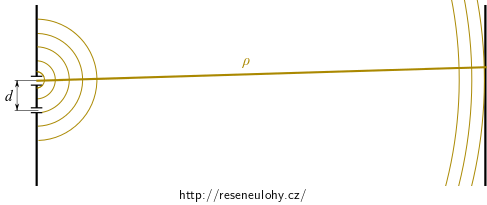
Nejprve nalezněme funkci vyjadřující závislost elektrické intenzity na čase, vzdálenosti a šířce štěrbiny. Jedná se o válcovou vlnu, jejíž amplituda klesá se vzdáleností a je závislá na šířce štěrbiny.
Tvar válcové vlny bez závislosti na šířce štěrbiny. \[E(\rho,t) \sim \frac{1}{\sqrt{\rho}} e^{i(\omega t - k\rho)}.\]
Intenzita světla \(I\) na stínítku je přímo úměrná šířce štěrbiny \(b\). Zároveň je intenzita \(I\) úměrná součinu \(EE^\star\). Elektrická intenzita je tedy úměrná odmocnině šířky štěrbiny
\[E(b) \sim \sqrt{b}.\]
Uvážením předchozích dvou závislostí a přidáním konstanty úměrnosti \(\mathcal{E}\), jejíž velikost souvisí s intenzitou na štěrbiny dopadající rovinné vlny, máme funkci
\[ E(t,\rho,b) = \mathcal{E} \sqrt{\frac{b}{\rho}} \, e^{i(\omega t - k\rho)} \]
Zjistíme celkovou elektrickou intenzitu, kterou dostaneme superpozicí příspěvků obou střebin pro závislost \(E(\rho, b, t)\).

Příspěvky od obou štěrbin na stínítku superponují. Předpokládáme-li, že vektory elektrických intenzit obou vln mají přibližně stejný směr, je výsledná intenzita součtem přímo velikostí \(E_1, E_2\)
\[ E = E_1 + E_2 = \mathcal{E} \left( \sqrt{\frac{b_1}{\rho_1}} \, e^{i(\omega t - k\rho_1)} + \sqrt{\frac{b_2}{\rho_2}} \, e^{i(\omega t - k\rho_2)} \right)= \]
protože je stínítko velmi daleko, je \(\rho_1 \approx \rho_2 \approx l\), kde \(l\) je vzdálenost stínítka a štěrbin, a proto
\[ =\mathcal{E}\frac{1}{\sqrt{l}} \left( \sqrt{b_1} \, e^{i(\omega t - k\rho_1)} + \sqrt{b_2} \, e^{i(\omega t - k\rho_2)} \right)= \]
dále vytkneme i \(\sqrt{b_1}\)
\[ =\mathcal{E}\sqrt{\frac{b_1}{l}} \bigg( e^{i(\omega t - k\rho_1)} + \underbrace{\sqrt{\frac{b_2}{b_1}}}_{\sqrt{p}} \, e^{i(\omega t - k\rho_2)} \bigg)= \]
a ve zbylém výrazu identifikujeme poměr šířek štěrbin \(\frac{b_2}{b_1} = p\). Máme tak
\[ E = \mathcal{E}\sqrt{\frac{b_1}{l}} \left( e^{i(\omega t - k\rho_1)} + \sqrt{p} e^{i(\omega t - k\rho_2)} \right). \]
Nyní chceme vyjádřit vztah výše, tak aby závisel na rozdílu \(\rho_1\), \(\rho_2\) a úhlu \(\theta\), který vyjadřuje úhel odklonu daného místa od normály roviny štěrbin.

Vytkněme ze závorky první člen dvojčlenu
\[ = \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{i(\omega t - k\rho_2)} e^{-i(\omega t - k\rho_1)} \right) = \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{ik(\rho_1 - \rho_2)} \right). \]
V závorce tak dostáváme dráhový rozdíl \(\Delta\rho = \rho_1 - \rho_2\).
\[ E= \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{ik\Delta \rho} \right). \]
Je-li stínítko velmi daleko od dvojštěrbiny a jsou-li štěrbiny dostatečně blízko, je směr průvodičů \(\rho_1\), \(\rho_2\) téměř rovnoběžný s jejich osou.

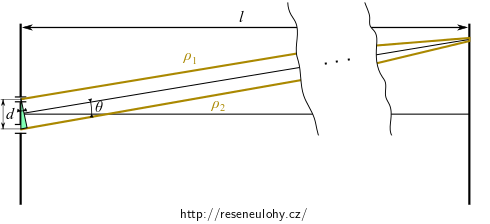
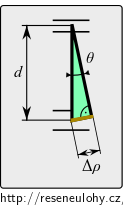
Dráhový rozdíl \(\Delta\rho\) je nejkratší strana v naznačeném zeleném trojúhelníku. Na obrázku vpravo je zvětšený.

Trojúhelník je v této aproximaci téměř pravoúhlý, proto
\[ \Delta \rho = d \sin \theta. \]
kde úhel \(\theta\) je současně odchylkou osy interferujících paprsků od normály stínítka.

Elektrická intenzita v místě stínítka určeném úhlem \(\theta\) je proto
\[ E= \mathcal{E}\sqrt{\frac{b_1}{l}}e^{i(\omega t - k\rho_1)} \left( 1 + \sqrt{p} e^{ikd\sin\theta} \right). \]
Určíme průběh relativní intenzity světla
\[ I \sim EE^\star = \mathcal{E}^2 \frac{b_1}{l} \underbrace{e^{i(\omega t - k\rho_1)}e^{-i(\omega t - k\rho_1)}}_{1} \left( 1 + \sqrt{p} e^{ikd\sin\theta} \right) \left( 1 + \sqrt{p} e^{-ikd\sin\theta} \right)= \] \[ = \mathcal{E}^2 \frac{b_1}{l} \left( 1 + \sqrt{p}e^{-ikd\sin\theta} + \sqrt{p}e^{ikd\sin\theta} + p \underbrace{e^{ikd\sin\theta} e^{-ikd\sin\theta} }_{1} \right) = \] \[ = \mathcal{E}^2 \frac{b_1}{l} \left[ 1 + p + \sqrt{p}\left( e^{ikd\sin\theta} + e^{-ikd\sin\theta} \right)\right]. \]
Výraz v kulaté závorce upravíme zvlášť.

Rozepsáním komplexních exponenciál z Eulerova vztahu \(\color{MidnightBlue}{e^{i\varphi} = \cos\varphi + i\sin\varphi}\) a úpravou
\[ e^{ikd\sin\theta} + \sqrt{p} e^{-ikd\sin\theta} = 2\cos (kd\sin\theta) \]

Dostáváme relativní závislost intenzity na úhlu \(\theta\)
\[ I_r(\theta) = 1 + p + 2\sqrt{p}\cos(kd\sin\theta) \]
Prověříme získanou funkci pro \(p=1\) a \(p \neq 1 \).

Funkce \(I_r(\theta)\) nabývá
\[ \begin{array}{lllll} \circ\ \text{maxima} & \text{pro} & \cos(kd\sin\theta) = 1 & \text{tj. když} & kd\sin\theta = 2\pi m,~m\in\mathbb{Z}\\ \circ\ \text{minima} & \text{pro} & \cos(kd\sin\theta) = -1 & \text{tj. když} & kd\sin\theta = \pi + 2\pi m,~m\in\mathbb{Z} \end{array} \]
tj. polohy minim a maxim nezávisí na poměru \(p\), obrazec se se změnou \(p\) nikam „neposouvá“. Co se může měnit, je však hodnota funkce, tj. intenzita.

Proveďme jednu „trikovou“ úpravu
\[ I_r(\theta) = 1 + p + 2\sqrt{p}\cos(kd\sin\theta) = 1 + p - \underbrace{2\sqrt{p} + 2\sqrt{p}}_{\text{odečtu a přičtu}} + 2\sqrt{p}\cos(kd\sin\theta) = \] \[ = 1 + p - 2\sqrt{p} + 2\sqrt{p}\left[1 + \cos(kd\sin\theta) \right] = 1 + p - 2\sqrt{p} + 4\sqrt{p}\frac{1 + \cos(kd\sin\theta) }{2} = \] \[ = \underbrace{1 + p - 2\sqrt{p}}_{\text{ozn. }I_\mathrm{min}} + 4\sqrt{p} \cos^2\left(\frac{kd\sin\theta}{2}\right). \]
Máme tedy ohybovou funkci ve tvaru
\[ I_r(\theta) = I_\mathrm{min}(p) + 4\sqrt{p} \cos^2\left(\frac{kd\sin\theta}{2}\right), \] \[ \text{kde}\quad I_\mathrm{min}(p) = 1 + p - 2\sqrt{p}. \]
Funkce \(I_\mathrm{min}(p)\) je nulová pouze pro \(p=1\), tj. v případě stejně širokých štěrbin, kdy se jedná o standardní Youngův experiment, jehož ohybový obrazec má nulová minima.

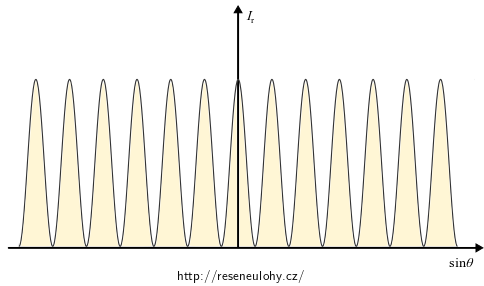
Jestliže je \(p\neq 1\), pak je funkce \(I_\mathrm{min}\) kladná a ohybový obrazec je posunutý ve směru kladné osy y, tj. má nenulová minima. Viz následující obrázek.

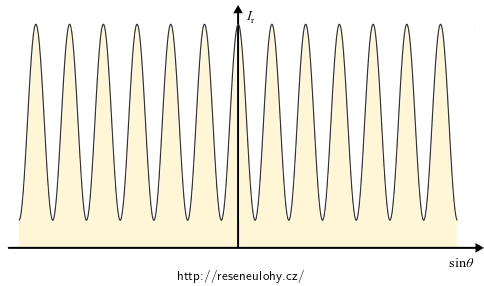
Funkce \(I_\mathrm{min}\) je rostoucí, tj. se zvětšováním poměru štěrbin \(p\) se zvětšuje i minimální hodnota intenzity na stínítku a současně pro \(p\gt 1\) se zvětšuje i obor hodnot celé ohybové funkce, tj. v maximech je dosahováno vyšších hodnot.
Odpověď
Relativní osvětlení stínítka popisuje funkce
\[ I_r(\theta) = 1 + p + 2\sqrt{p}\cos(kd\sin\theta), \]
kde \(p\) je poměr šířek štěrbin, \(k\) velikost vlnového vektoru, \(d\) vzdálenost štěrbin a \(\theta\) úhel určující místo na stínítku.

Případ \(p=1\):

Případ \(p\gt 1\):
Poznámka
Ověřme, že amplituda elektrické intenzity válcové vlny klesá s \(\sqrt{\rho}\), tj. že
\[E \sim \frac{1}{\sqrt{\rho}} e^{i(\cdots)}.\] Je-li tomu tak, pak by měla intenzita světla \(I\) klesat s první mocninou vzdálenosti \(\rho\), neboť \[I \sim EE^\star \sim \frac{1}{\sqrt{\rho}}\frac{1}{\sqrt{\rho}} \underbrace{e^{i(\cdots)} e^{-i(\cdots)}}_{1} \sim \frac{1}{\rho}.\tag{7}\]
Je to správně?
Přímkový zdroj vyzáří za jednotku času energii \(E\). Tato energie se musí „rozložit“ na válcovou plochu, která roste s jejím poloměrem \(\rho\) (obsah pláště válce \(S = 2\pi \rho h\)). Energie připadající na jeden metr čtvereční (za jednotku času), tedy intenzita \(I\), proto s \(\rho\) klesá, což je v souladu s (7). Pokles \(E\) s \(\sqrt\rho\) je tak správný.