Youngův pokus

Úloha číslo: 1502

Stanovte průběh intenzity světla na stínítku při Youngově interferenčním pokusu za podmínky, že obě štěrbiny, sloužící jako koherentní zdroje světla, jsou velmi úzké ve srovnání s jejich vzájemnou vzdáleností.

Určete také šířku inteferenčních proužků.

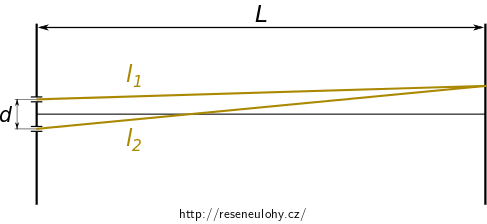
Stínítko je umístěno ve vzdálenosti \(L\) od clony a je s ní rovnoběžné. Vzdálenost štěrbin je \(d\). Na štěrbiny dopadá kolmo rovinná harmonická vlna.

Štěrbiny považujte za velmi úzké (aby první minimum ohybového jevu na štěrbině bylo daleko mimo stínítko). Jinak řečeno předpokládejte, že při osvětlení jen jedné štěrbiny by díky ohybu na ní bylo osvětlení stínítka rovnoměrné.
Řešte v aproximaci Fraunhoferova ohybu, \(L\gg d\).

Teorie a vztahy potřebné pro řešení úlohy
• Při výpočtu budeme používat komplexní formalismus, s nímž jsme se seznámili zde a pracovali jsme s ním v této úloze.

• Úlohu máme řešit v aproximaci tzv. Fraunhoferova ohybu, tj. interferenční obrazec budeme zkoumat na velmi vzdáleném stínítku. Právě díky této podmínce lze při výpočtu přistoupit k řadě zjednodušení.

• Štěrbiny jsou velmi úzké, budeme tedy předpokládat, že při osvětlení jen jedné štěrbiny by díky ohybu na ní bylo osvětlení stínítka rovnoměrné. Na štěrbiny proto budeme nahlížet jako na přímkové zdroje válcových vln. Elektrická intenzita vlny v místě vzdáleném \(\rho\) od zvolené štěrbiny je tedy
\[E_\mathrm{valc}(t,\rho) = \frac{\mathcal{E}_0}{\sqrt{r}} e^{i(\omega t - k\rho )},\]
kde \(\mathcal{E}_0\) je veličina, jejíž velikost souvisí s intenzitou na štěrbiny dopadající rovinné vlny a šířkou štěrbiny.

• Intenzitu světla ve velké vzdálenosti, kde lze lokálně části válcových vln považovat za rovinné, vypočítáme pomocí vztahu
\[ I = \frac{1}{2z_0} EE^\star, \]
kde hvězdička značí komplexní sdružení a \(z_0 = \sqrt{\frac{\mu_0}{\varepsilon_0}}\) je impedance vakua.

• Pro malé úhly \(\delta \ll 1\) je
\[ \sin\delta \,\approx\, \tan \delta . \]
Nápověda 1 – superpozice elektrických intenzit
Určete velikost elektrické intenzity vlny vzniklé součtem vln s průvodiči \(l_1\) a \(l_2\).

Připravte si také komplexně sdruženou výslednou elektrickou intenzitu \(E^\star\).
Řešení nápovědy 1 – superpozice elektrických intenzit
Velikost elektrické intenzity vlny z první štěrbiny v daném místě stínítka, vzdáleném \(l_1\) od této štěrbiny je
\[ E_1 = \frac{\mathcal{E}_0}{\sqrt{l_1}} e^{i(\omega t - kl_1)} ~\approx~ \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)}, \]
a intenzita ve stejném místě od druhé štěrbiny, vzdálené \(l_2\) je
\[ E_2 = \frac{\mathcal{E}_0}{\sqrt{l_2}} e^{i(\omega t - kl_2)} ~\approx~ \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_2)}. \]
Neboť budeme uvažovat velmi vzdálené stínítko, faktory \(\sqrt{l_1}, \sqrt{l_2}\) úbytku amplitud elektrických intenzit jsme aproximovali hodnotou \({\sqrt {L}}\).

Výsledná intenzita v daném místě na stínítku je vektorovým součtem těchto intenzit.

Aby bylo možné velikosti elektrických intenzit sčítat přímo skalárně, musely by mít vektory elektrické intenzity válcových vln z obou štěrbin v uvažovaném místě stínítka stejný směr. To je ale přibližně splněno, neboť při velmi vzdáleném a dostatečně malém stínítku jsou průvodiče od obou štěrbin téměř rovnoběžné, válcové vlnoplochy jsou téměř rovinné.

Postupnými úpravami dostaneme
\[ E = E_1 + E_2 = \frac{\mathcal{E}_0}{\sqrt{L}} \left( e^{i(\omega t - kl_1)} + e^{i(\omega t - kl_2)}\right) = \] \[ =\frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \big(1 + e^{-ik(\overbrace{l_2-l_1}^{\mathrm{ozn.\,}\Delta l})} \big)= \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \left(1 + e^{-ik\Delta l} \right). \]
Komplexně sdružená velikost výsledné elektrické intenzity je
\[ E^\star=\frac{\mathcal{E}_0}{\sqrt{L}} e^{-i(\omega t - kl_1)} \left(1 + e^{ik\Delta l} \right). \]
Nápověda 2 – průběh intenzity na stínítku
Uvažte, že se jedná o velmi dlouhé štěrbiny ve srovnání s jejich šířkou. Je nutné určovat intenzitu pro každý bod na stínítku?

Určete závislost intenzity světla při daném dráhovém rozdílu \(\Delta l\) podle vztahu
\[ I = \frac{1}{2z_0} EE^\star, \]
dosazením právě vypočítané elektrické intenzity a jejího komplexního sdružení.
Řešení nápovědy 2 – průběh intenzity na stínítku
V aproximaci nekonečně dlouhých štěrbin musí mít interferenční obrazec translační symetrii podél směru rovnoběžného s délkou štěrbin. Úlohu tedy stačí řešit v rovině nákresny, protože rozložení osvětlení na stínítku bude všude na kolmici k nákresně stejné jako v jejím průsečíku s nákresnou.

Vypočítané elektrické intenzity dosadíme do vztahu pro intenzitu světla
\[ I = \frac{1}{2z_0} EE^\star = \frac{\mathcal{E}_0^2}{2z_0 L} \underbrace{e^{i(\omega t - kl_1)} e^{-i(\omega t - kl_1)}}_{1} \left(1 + e^{-ik\Delta l} \right)\left(1 + e^{ik\Delta l} \right)= \] \[ \frac{\mathcal{E}_0^2}{2z_0 L} \big(1 + e^{ik\Delta l} + e^{-ik\Delta l} + \underbrace{e^{-ik\Delta l} e^{ik\Delta l}}_{1} \big) = \frac{\mathcal{E}_0^2}{2z_0 L} \left(2+ e^{ik\Delta l} + e^{-ik\Delta l}\right)= \]
Výraz ještě upravíme přepsáním komplexních exponenciál do goniometrického tvaru dle vztahu \(e^{i\varphi} = \cos \varphi + i\sin\varphi\).
\[ =\frac{\mathcal{E}_0^2}{2z_0 L} \left(2+\cos k \Delta l + i \sin k \Delta l + \cos k \Delta l - i \sin k \Delta l \right) = \] \[ = \frac{\mathcal{E}_0^2}{z_0 L}\left(1+\cos k \Delta l \right)= \frac{2\mathcal{E}_0^2}{z_0 L}\cos^2 \left(\frac{k \Delta l}{2} \right). \tag{1}\]
V posledním kroku jsme použili goniometrický vztah \(\small \cos^2 \frac{x}{2} = \frac{1}{2}\left(1+\cos x\right)\).
Nápověda 3 – určení dráhového rozdílu
Uvažujte, že stínítko je velmi daleko od dvojštěrbiny.

Vyjádřete dráhový rozdíl \(\Delta l\) pomocí vzdálenosti štěrbin \(d\) a odchylky \(\alpha\) osy interferujících paprsků od normály stínítka.
Řešení nápovědy 3 – určení dráhového rozdílu
Je-li stínítko velmi daleko od dvojštěrbiny a jsou-li štěrbiny dostatečně blízko, je směr průvodičů \(l_1\) a \(l_2\) téměř rovnoběžný s jejich osou.

Dráhový rozdíl \(\Delta l\) je nejkratší strana v naznačeném zeleném trojúhelníku. Na obrázku vpravo je zvětšený.

Trojúhelník je v této aproximaci pravoúhlý, proto
\[ \Delta l = d \sin \alpha, \]
kde úhel \(\alpha\) je současně odchylkou osy interferujících paprsků od normály stínítka.

Dosazením do vztahu (1) pro intenzitu máme
\[ I = \frac{2\mathcal{E}_0^2}{z_0 L}\cos^2 \left(\frac{kd \sin \alpha}{2} \right). \tag{2}\]
Graf funkce \(I=I(\sin\alpha)\).

Vykreslili jsme závislost intenzity světla jako funkci výrazu \(\sin \alpha\), který je úměrný souřadnici \(x\).

Podle grafu intenzita s rostoucí vzdáleností od středu stínítka globálně neubývá, což souvisí s tím, že štěrbiny jsou velmi úzké – pohybujeme se stále v oblasti centrálního ohybového maxima.
Nápověda 4 – šířka interferenčních proužků
Pro malé úhly \(\alpha\) určete šířku proužku interferenčního obrazce.

Jak závisí šířka obrazce na \(L,\lambda\) a \(d\)?
Řešení nápovědy 4 – šířka interferenčních proužků
Ještě určíme šířku proužků interferenčního obrazce, tj. vzdálenost sousedních minim (maxim). Přistoupíme k další aproximaci, pro malé úhly \(\alpha \ll 1\) je
\[\sin\alpha \,\approx\,\tan \alpha = \frac{x}{L}.\]

Dosazením \(\frac{x}{L}\) za \(\sin\alpha\) ve vztahu (2) máme
\[ I = \frac{2\mathcal{E}_0^2}{z_0 L}\cos^2 \left(\frac{kdx}{2L} \right), \qquad \mathrm{pro~}\alpha \ll 1. \]

První minimum intenzity nastává pro argument \(\frac{\pi}{2}\). Určeme v jaké souřadnici \(x=p\) na stínítku k tomu dochází. Použijeme vztah \(k=\frac{2\pi}{\lambda}\).
\[ \frac{2\pi}{\lambda}\frac{d p}{2L} = \frac{\pi}{2} \quad \Rightarrow \quad p = \frac{L\lambda}{2d}. \]
Vzdálenost sousedních minim (maxim) je dvojnásobná, tj. šířka proužku je
\[ s = 2p = \frac{L\lambda}{d}. \]
Se zvětšující se vzdáleností \(L\) stínítka od štěrbiny a s rostoucí vlnovou délkou \(\lambda\) se bude interferenční obrazec rozšiřovat, se zvětšováním vzdálenosti štěrbin \(d\) se bude naopak zhušťovat.
CELKOVÉ ŘEŠENÍ
Velikost elektrické intenzity vlny z první štěrbiny v daném místě stínítka, vzdáleném \(l_1\) od této štěrbiny je
\[ E_1 = \frac{\mathcal{E}_0}{\sqrt{l_1}} e^{i(\omega t - kl_1)} ~\approx~ \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)}, \]
a intenzita ve stejném místě od druhé štěrbiny, vzdálené \(l_2\) je
\[ E_2 = \frac{\mathcal{E}_0}{\sqrt{l_2}} e^{i(\omega t - kl_2)} ~\approx~ \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_2)}. \]
Neboť budeme uvažovat velmi vzdálené stínítko, faktory \(\sqrt{l_1}, \sqrt{l_2}\) úbytku amplitud elektrických intenzit jsme aproximovali hodnotou \({\sqrt {L}}\).

Výsledná intenzita v daném místě na stínítku je vektorovým součtem těchto intenzit.

Aby bylo možné velikosti elektrických intenzit sčítat přímo skalárně, musely by mít vektory elektrické intenzity válcových vln z obou štěrbin v uvažovaném místě stínítka stejný směr. To je ale přibližně splněno, neboť při velmi vzdáleném a dostatečně malém stínítku jsou průvodiče od obou štěrbin téměř rovnoběžné, válcové vlnoplochy jsou téměř rovinné.

Postupnými úpravami dostaneme
\[ E = E_1 + E_2 = \frac{\mathcal{E}_0}{\sqrt{L}} \left( e^{i(\omega t - kl_1)} + e^{i(\omega t - kl_2)}\right) = \] \[ =\frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \big(1 + e^{-ik(\overbrace{l_2-l_1}^{\mathrm{ozn.\,}\Delta l})} \big)= \frac{\mathcal{E}_0}{\sqrt{L}} e^{i(\omega t - kl_1)} \left(1 + e^{-ik\Delta l} \right). \]
Komplexně sdružená velikost výsledné elektrické intenzity je
\[ E^\star=\frac{\mathcal{E}_0}{\sqrt{L}} e^{-i(\omega t - kl_1)} \left(1 + e^{ik\Delta l} \right). \]
Vypočítané elektrické intenzity dosadíme do vztahu pro intenzitu světla
\[ I = \frac{1}{2z_0} EE^\star = \frac{\mathcal{E}_0^2}{2z_0 L} \underbrace{e^{i(\omega t - kl_1)} e^{-i(\omega t - kl_1)}}_{1} \left(1 + e^{-ik\Delta l} \right)\left(1 + e^{ik\Delta l} \right)= \] \[ =\frac{\mathcal{E}_0^2}{2z_0 L} \big(1 + e^{ik\Delta l} + e^{-ik\Delta l} + \underbrace{e^{-ik\Delta l} e^{ik\Delta l}}_{1} \big) = \frac{\mathcal{E}_0^2}{2z_0 L} \left(2+ e^{ik\Delta l} + e^{-ik\Delta l}\right)= \]
Výraz ještě upravíme přepsáním komplexních exponenciál do goniometrického tvaru dle vztahu \(e^{i\varphi} = \cos \varphi + i\sin\varphi\).
\[ =\frac{\mathcal{E}_0^2}{2z_0 L} \left(2+\cos k \Delta l + i \sin k \Delta l + \cos k \Delta l - i \sin k \Delta l \right) = \] \[ = \frac{\mathcal{E}_0^2}{z_0 L}\left(1+\cos k \Delta l \right)= \frac{2\mathcal{E}_0^2}{z_0 L}\cos^2 \left(\frac{k \Delta l}{2} \right). \tag{1}\]
V posledním kroku jsme použili goniometrický vztah \(\small \cos^2 \frac{x}{2} = \frac{1}{2}\left(1+\cos x\right)\).

Je-li stínítko velmi daleko od dvojštěrbiny a jsou-li štěrbiny dostatečně blízko, je směr průvodičů \(l_1\) a \(l_2\) téměř rovnoběžný s jejich osou.

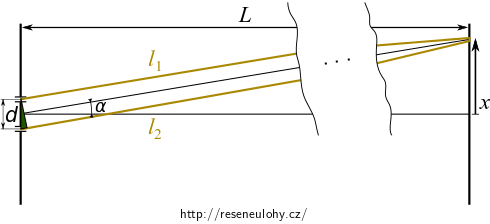
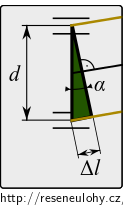
Dráhový rozdíl \(\Delta l\) je nejkratší strana v naznačeném zeleném trojúhelníku. Na obrázku vpravo je zvětšený.

Trojúhelník je v této aproximaci pravoúhlý, proto
\[ \Delta l = d \sin \alpha, \]
kde úhel \(\alpha\) je současně odchylkou osy interferujících paprsků od normály stínítka.

Dosazením do vztahu (1) pro intenzitu máme
\[ I = \frac{2\mathcal{E}_0^2}{z_0 L}\cos^2 \left(\frac{kd \sin \alpha}{2} \right). \tag{2}\]
Graf funkce \(I=I(\sin\alpha)\).

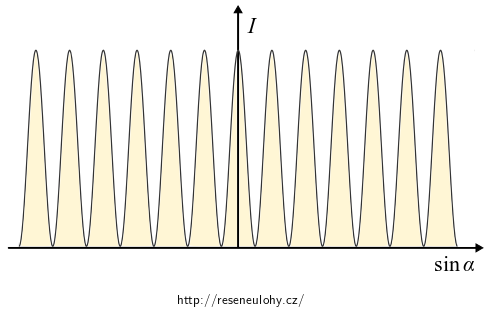
Vykreslili jsme závislost intenzity světla jako funkci výrazu \(\sin \alpha\), který je úměrný souřadnici \(x\).

Podle grafu intenzita s rostoucí vzdáleností od středu stínítka globálně neubývá. Je to proto, že jsme neuvažovali ohyb na štěrbinách.

Ještě určíme šířku proužků interferenčního obrazce, tj. vzdálenost sousedních minim (maxim). Přistoupíme k další aproximaci, pro malé úhly \(\alpha \ll 1\) je
\[\sin\alpha \,\approx\,\tan \alpha = \frac{x}{L}.\]

Dosazením \(\frac{x}{L}\) za \(\sin\alpha\) ve vztahu (2) máme
\[ I = \frac{2\mathcal{E}_0^2}{z_0 L}\cos^2 \left(\frac{kdx}{2L} \right), \qquad \mathrm{pro~}\alpha \ll 1. \]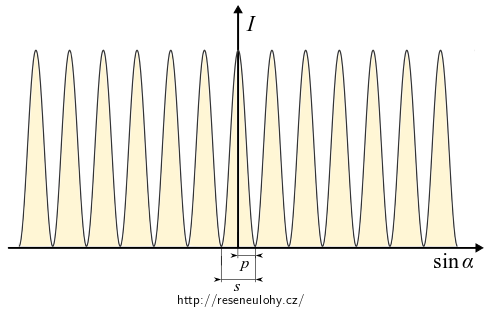

První minimum intenzity nastává pro argument \(\frac{\pi}{2}\). Určeme v jaké souřadnici \(x=p\) na stínítku k tomu dochází. Použijeme vztah \(k=\frac{2\pi}{\lambda}\).
\[ \frac{2\pi}{\lambda}\frac{d p}{2L} = \frac{\pi}{2} \quad \Rightarrow \quad p = \frac{L\lambda}{2d}. \]
Vzdálenost sousedních minim (maxim) je dvojnásobná, tj. šířka proužku je
\[ s = 2p = \frac{L\lambda}{d}. \]
Se zvětšující se vzdáleností \(L\) stínítka od štěrbiny a s rostoucí vlnovou délkou \(\lambda\) se bude interferenční obrazec rozšiřovat, se zvětšováním vzdálenosti štěrbin \(d\) se bude naopak zhušťovat.
Odpověď
Při aproximaci na vzdálené stínítko jsme dostali následující průběh intenzity
\[ I = \frac{2\mathcal{E}_0^2}{z_0 L}\cos^2 \left(\frac{kd \sin \alpha}{2} \right), \]
kde \(\alpha\) je úhel, který svírá normála stínítka s osou interferujících paprsků.

Graf \(I=I(\sin\alpha)\).

Námi vypočítaný průběh intenzity, jak jej vidíme na grafu, bude dobře popisovat oblast v blízkosti středu stínítka. Ve vzdálenějších oblastech od středu se již bude projevovat pokles intenzit hlavních maxim, způsobený ohybem na štěrbinách.

Určili jsme souvislost šířky interferenčních proužků a ostatních parametrů
\[ s \,\approx\, \frac{\lambda L}{d}. \]
Se zvětšující se vzdáleností \(L\) stínítka od štěrbiny a s rostoucí vlnovou délkou \(\lambda\) se bude interferenční obrazec rozšiřovat, se zvětšováním vzdálenosti štěrbin \(d\) se bude naopak zhušťovat.
Odkaz – Youngův pokus s ohybem
Youngův interferenční pokus s uvažováním ohybu na štěrbinách naleznete v úloze Ohyb na dvojité štěrbině.
Odkaz na pokus
Pokud vás zajímá, jak vypadá interferenční obrazec na stínítku ve skutečnosti, podívejte se na Dvojštěrbinový pokus.