Sbírka řešených úloh

Výpočet maximálního řádu spektra a rozlišovací schopnosti

Úloha číslo: 1666

• Nápověda 1 – výpočet řádu maxima

  Jaký vztah platí pro interferenční maxima při interferenci na mřížce?

• Řešení nápovědy 1 – výpočet řádu maxima

  Pro interferenční maxima na mřížce platí vztah:

  \[b\sin\,\alpha=k\lambda,\]

  kde b je mřížková konstanta, α je úhel odchýlení, k je řád maxima a λ je vlnová délka dopadajícího světla.

  Podrobné vysvětlení najdete v úloze Výpočet úhlu odchýlení maxima.

• Nápověda 2 – výpočet řádu maxima

  Jakých hodnot může nabývat úhel odchýlení α a co to říká o interferenčních maximech?

• Řešení nápovědy 2 – výpočet řádu maxima

  Úhel odchýlení α se pohybuje od 0° do 90°. Vyjádříme si řád maxima k z rovnice v předchozí nápovědě, získáme:

  \[k=\frac{b\sin\,\alpha}{\lambda}\le \frac{b\sin90\,^\circ}{\lambda}=\,\frac{b}{\lambda},\]

  kam dosadíme hodnoty a vypočítáme nejvyšší řád interferenčního maxima.

• Nápověda 3

  Co je to rozlišovací schopnost a jak se vypočítá?

• Řešení nápovědy 3

  Rozlišovací schopnost A souvisí s tím, kdy jsme ještě schopni rozeznat dvě vlnové délky, které jsou blízko u sebe. Je definována jako:

  \[A=\,\frac{\lambda}{\mathrm{d}\lambda}\]

  v případě, že jsme schopni rozlišit vlnovou délku λ a λ + dλ, tzv. Rayleighovo kritérium.

   

  Podívejme se na to, jak vypadá průběh intenzity světla na stínítku podrobněji (podrobně je mřížka vysvětlena v úloze Difrakce na mřížce): \[I \approx \frac{\sin^2 \frac{N\kappa b\sin\alpha}{2}}{\sin^2 \frac{\kappa b\sin\alpha}{2}} \tag{2},\] kde α je úhel odchýlení, b mřížková konstanta, \(\kappa = \frac{2 \pi}{\lambda}\) velikost vlnového vektoru a N počet osvětlených vrypů.

  

  Na obrázku je průběh intenzity světla pro ideální mřížku s pěti vrypy.

  Hranicí pro rozlišení dvou spektrálních čar rozumíme případ, kdy hlavní maximum intenzity světla jedné vlnové délky padne právě do nejbližšího minima (místa s nulovou hodnotou) druhé vlnové délky.

  Hlavní maxima se vyskytují v polohách, pro něž jmenovatel výše uvedeného vztahu je nulový (konečnost intenzity je dokázána zde): \[\frac{\kappa b\sin\alpha}{2} = k \pi \qquad\Rightarrow\qquad b\sin\alpha = k\lambda,\] kde k je řád maxima. Mezi hlavními maximy je (N − 1) míst s nulovou intenzitou (minim) daných podmínkou, že čitatel je nulový \[\frac{N \kappa b\sin\alpha}{2} = K \pi \qquad\Rightarrow\qquad b\sin\alpha = \frac{K\lambda}{N},\] kde K je pořadí minima. Odtud je vidět, že vzdálenost minim na ose \(b \sin \alpha\) je \(\frac{\lambda}{N}\) stejně jako vzdálenost prvního minima od hlavního maxima.

  Vezmeme si 2 vlnové délky λ₁ a λ₂ a napíšeme si podmínku pro hlavní interferenční maximum pro první vlnovou délku:

  \[b\sin\,\alpha_1 =\,k\lambda_\mathrm{1},\]

  a podmínku prvního minima pro vlnovou délku λ₂:

  \[b\sin\,\alpha_2=\,k\lambda_\mathrm{2} + \frac{\lambda_\mathrm{2}}{N}. \]

   

  Nyní si uvědomíme, že úhel pro maximum jedné vlnové délky se musí rovnat úhlu pro minimum druhé vlnové délky, tedy se zobrazí ve stejném místě, tedy α₁ = α₂. Pokud se rovnají úhly, rovnají se i hodnoty jejich sinů. Získáme tedy rovnici:

  \[k\lambda_\mathrm{1}=\,k\lambda_\mathrm{2} + \frac{\lambda_\mathrm{2}}{N}, \]

  kterou upravíme, abychom dostali vztah pro rozlišovací schopnost A:

  \[k(\lambda_\mathrm{1} − \lambda_\mathrm{2})=\,\frac{\lambda_\mathrm{2}}{N},\]

  kde λ₁ − λ₂ si označíme jako dλ a upravíme do tvaru:

  \[A=\,\frac{\lambda}{\mathrm{d}\lambda}=\, kN.\]

• Zápis

  N = 800	počet vrypů na 1 mm
  λ = 500 nm = 5,0·10−7 m	vlnová délka dopadajícího světla
  L = 5 cm = 50 mm	délka mřížky
  k = ?	nejvyšší řád maxima, který můžeme pozorovat
  A = ?	rozlišovací schopnost

• Řešení

  Pro výpočet řádu maxima budeme potřebovat rovnici pro mřížku, která počítá s dráhovým rozdílem paprsků a s mřížkovou konstantou, tedy:

  \[b\sin\,\alpha=k\lambda,\]

  kde b je mřížková konstanta, k je řád maxima, λ je vlnová délka světla a α je úhel ochýlení. Z této rovnice si vyjádříme řád maxima k a získáme:

  \[k=\,\frac{b\sin\,\alpha}{\lambda}.\]

  Pokud se zamyslíme nad úhlem odchýlení α, mělo by nás napadnout, že tento úhel nemůže být větší než 90°, tím získáme nerovnost:

  \[k=\frac{b\sin\,\alpha}{\lambda}\le \frac{b\sin\,90}{\lambda}=\,\frac{b}{\lambda},\]

  kde b si vypočítáme pomocí vztahu:

  \[b=\,\frac{10^\mathrm{−3}\,\mathrm{m}}{N}=\,\frac{10^\mathrm{−3}\,\mathrm{m}}{800}\]

  Nyní dosadíme hodnoty a vypočítáme nejvyšší řád interferenčního maxima, který můžeme pozorovat.

  \[k=\,\frac{\frac{10^\mathrm{−3}\,\mathrm{m}}{800}}{5{,}0{\cdot}10^\mathrm{−7}\,\mathrm{m}}=\,\frac{10^\mathrm{−3}\,\mathrm{m}}{800{\cdot}5{,}0{\cdot}10^\mathrm{−7}\,\mathrm{m}}=\,2{,}5.\]

  Protože k má být celé číslo, řešení je tedy k = 2.

   

  Rozlišovací schopnost A je definována jako:

  \[A=\,\frac{\lambda}{\mathrm{d}\lambda}.\]

  Hranicí pro rozlišení dvou spektrálních čar zdálených od sebe o Δλ je případ, kdy hlavní maximum intenzity světla jedné vlnové délky padne právě do nejbližšího minima (místa s nulovou hodnotou) druhé vlnové délky.

  Podíváme se, jak vypadá průběh intenzity světla na stínítku podrobněji: \[I \approx \frac{\sin^2 \frac{N\kappa b\sin\alpha}{2}}{\sin^2 \frac{\kappa b\sin\alpha}{2}}. \tag{2},\] kde α je úhel odchýlení, b mřížková konstanta, \(\kappa = \frac{2 \pi}{\lambda}\) velikost vlnového vektoru a N počet osvětlených vrypů.

  

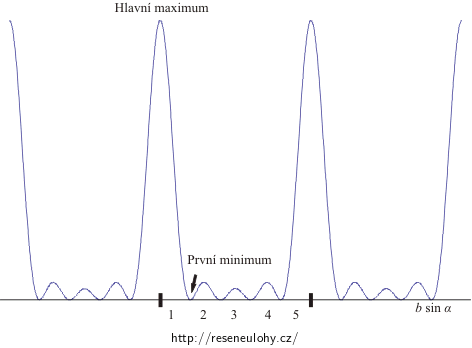
  Na obrázku je průběh intenzity světla pro ideální mřížku s pěti vrypy.

  Polohu hlavních maxim určuje podmínka: \[\frac{\kappa b\sin\alpha}{2} = k \pi \qquad\Rightarrow\qquad b\sin\alpha = k\lambda,\] kde k je řád maxima. Vzdálenost minim na ose \(b \sin \alpha\) je \(\frac{\lambda}{N}\) stejně jako vzdálenost prvního minima od hlavního maxima. Podrobněji viz Napověda 3.

  Pro dvě vlnové délky λ₁ a λ₂ napíšeme podmínku pro hlavní interferenční maximum pro první vlnovou délku:

  \[b\sin\,\alpha_1 =\,k\lambda_\mathrm{1},\]

  a podmínku prvního minima pro vlnovou délku λ₂:

  \[b\sin\,\alpha_2=\,k\lambda_\mathrm{2} + \frac{\lambda_\mathrm{2}}{N_\mathrm{c}}, \]

  kde N_c je celkový počet vrypů na celé dýlce mřížky.

  Nyní si uvědomíme, že úhel pro maximum jedné vlnové délky se musí rovnat úhlu pro minimum druhé vlnové délky, tak se zobrazí ve stejném místě, tedy α₁ = α₂. Pokud se rovnají úhly, rovnají se i hodnoty jejich sinů. Získáme tedy rovnici:

  \[k\lambda_\mathrm{1}=\,k\lambda_\mathrm{2} + \frac{\lambda_\mathrm{2}}{N_\mathrm{c}}, \]

  ze které vyjádříme k:

  \[k(\lambda_\mathrm{1} − \lambda_\mathrm{2})=\,\frac{\lambda_\mathrm{2}}{N_\mathrm{c}},\]

  kde λ₁ − λ₂ si označíme jako dλ a upravíme do tvaru:

  \[A=\,\frac{\lambda}{\mathrm{d}\lambda}=\, kN_\mathrm{c},\]

  kde k je nejvyšší pozorovaný řád a N_c je celkový počet vrypů na mřížce.

  Celkový počet vrypů N_c na mřížce vypočítáme jako počet vrypů na 1 mm krát délky mřížky:

  \[N_\mathrm{c}=\,LN=\,50{\cdot}800=\,40\,000 \,\mathrm{vrypů}\]

  Dosadíme hodnoty ze zadání a vypočítáme:

  \[A=\, kN_\mathrm{c}=\, 2\,\cdot\,800\,\cdot\,50=\,80\, 000=\,8{\cdot}10^\mathrm{4}.\]

• Odpověď

  Můžeme pozorovat dva řády interference a rozlišovací schopnost v nejvyšším, tedy druhém, řádu je 8·10⁴.