Sbírka řešených úloh

CD jako tenká vrstva

Úloha číslo: 1631

Záznam informace na kompaktním disku (CD) je proveden v hliníkové odrazné vrstvě řadou různě dlouhých oválných důlků. Pokud kruhová světelná stopa infračerveného laseru přehrávače dopadá do oblasti důlku, část záření se odrazí z jeho dna, část z jeho okolí – viz obrázek. Hloubka důlku je volena tak, aby se obě části odraženého záření rušily. Jakou hloubku by měly mít důlky na kompaktním disku? Laser přehrávače využívá vlnovou délku 0,78 µm, index lomu plastového materiálu CD je 1,5.

Obrázek znázorňuje pohled shora na důlky a stopu laseru.

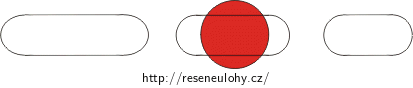
Obrázek znázorňuje pohled na důlky z boku a dopad laserového svazku do jednoho důlku.

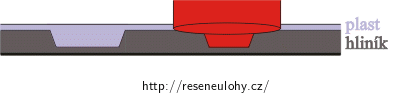
• Obrázek chodu interferujících paprsků

  

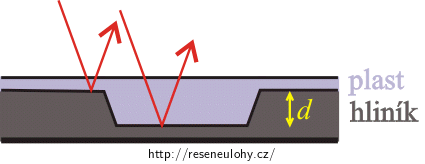
  Na obrázku jsme hloubku důlku v hliníkovém materiálu CD označili d a červeně jsou zakresleny paprsky, které přicházejí od zdroje.

• Nápověda 1

  Jakou dráhu musel urazit paprsek, který dopadne do důlku, a jakou dráhu urazil paprsek, který se odrazí mimo důlek? O co se tyto dráhy liší a jaký je jejich dráhový rozdíl?

• Řešení nápovědy 1

  Pro určení drah se podíváme do obrázku.

  

  Pokud si správně nakreslíme obrázek, uvidíme, že oba paprsky musí projít vzduchem a plastovým materiálem a pak se odrazí na hliníku. Paprsek, který dopadá do důlku, musí v plastu projít delší dráhu než paprsek, který se odrazí mimo důlek.

  Jejich dráhy se liší o dráhu, kterou paprsek urazil, když prošel důlkem tam a zpět. Tento dráhový rozdíl odpovídá optické dráze o velikosti:

  \[\mathrm{\Delta}l =\, \mathrm{2}nd.\]

  Změnu fáze při odrazu nemusíme uvažovat, protože se odrážejí oba paprsky, a tedy nedojde k ovlivnění jejich vzájemného rozdílu optických drah.

  Pro podrobné vysvětlení se podívejte na úlohu Vrstva oleje na vodě.

• Nápověda 2

  Jaká podmínka platí pro interferenční minima?

• Řešení nápovědy 2

  Protože se mají oba odražené paprsky vyrušit, musí nastat interferenční minimum. Paprsky se tedy setkají v opačných fázích, tj. jejich dráhový rozdíl bude lichým násobkem poloviny vlnové délky:

  \[ \mathrm{\Delta}l = (2k + 1)\, \frac{\lambda}{2},\]

  kde k je řád minima a platí, že k = 0, 1, 2, 3,...

  Chceme, aby důlky byly co nejméně hluboké, a proto za k dosadíme 0.

• Zápis

  λ = 0,78 µm  = 7,8·10−7 m	vlnová délka infračerveného laseru
  n = 1,5	relativní index lomu plastového materiálu CD
  d = ? (µm)	hloubka důlků

• Řešení

  

  Na obrázku jsme hloubku důlku v hliníkovém materiálu CD označili d a červeně jsou zakresleny paprsky, které přicházejí od zdroje.

  Nejprve zkusme zjistit, o jakou dráhu se liší dva paprsky, z nichž jeden se odrazil mimo důlek a druhý se odrazil v důlku. Oba paprsky musí pojít vzduchem a plastem. Ale paprsek, který projde do důlku a zpět, urazí v plastu delší dráhu. Rozdíl optických drah odpovídá:

  \[\mathrm{\Delta}l =\, \mathrm{2}nd.\]

  Protože se mají oba odražené paprsky vyrušit, nastává interferenční minimum, pro které platí vztah:

  \[ \mathrm{\Delta}l = (2k + 1)\,\frac{\lambda}{2},\]

  kde k je celé číslo. Pokud chceme, aby důlky byly co nejméně hluboké, za k dosadíme 0.

  Nyní dosadíme do předchozí rovnice za k = 0 a za rozdíl optických drah Δl = 2nd. Získáme vztah:

  \[ \mathrm{2}nd =\,\frac{\lambda}{2},\]

  ze kterého si vyjádříme d a dosadíme hodnoty ze zadání.

  \[d =\,\frac{\lambda}{\mathrm{4}n}= \,\frac{7{,}8{\cdot}10^{−7}}{4\,\cdot\,1{,}5}\, \mathrm{m} = 1{,}3{\cdot}10^{−7} \,\mathrm{m} = 0{,}13\, \mathrm{µm}. \]

• Odpověď

  Hloubka důlků na CD je 0,13 µm.