Zpoždění západu Slunce
Úloha číslo: 1407
Pro pozorovatele na Zemi právě nastal západ Slunce. V důsledku lomu slunečních paprsků na rozhraní vakua a atmosféry je západ pozorován později, než kdyby toto rozhraní neexistovalo. Určete toto zpoždění.
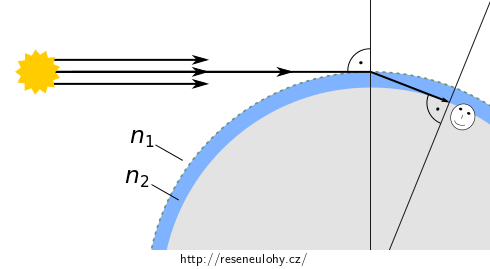
Rozhraní vakua a atmosféry není ostré. Při výpočtu ale užijte značně zjednodušující model, viz obrázek. Uvažujte jedno sférické rozhraní dvou izotropních prostředí, vakua (\(n_1=1\)) a idealizované atmosféry (\(n_2=1{,}0003\)), jejíž tloušťka je právě taková, že paprsky na rozhraní dopadají pod pravým úhlem.
Nápověda 1 – zakreslení situace
Nakreslete si obrázek, který znázorňuje mezní případ západu Slunce pro pozorovatele na Zemi. Zaneste úhel dopadu a úhel lomu.
Uvědomte si, že šířka atmosféry je pouze zlomkem poloměru Země.
Nápověda 2 – úhel lomu
Jaký je v mezní situaci úhel dopadu? Vyjádřete jej ze Snellova zákona lomu.
Nápověda 3 – časové zpoždění
• Ve kterém místě by člověk pozoroval západ Slunce, pokud by neexistovala atmosféra, tedy žádné rozhraní?
• Jaký úhel otočení Země tomu odpovídá?
• Jaký čas na toto pootočení Země potřebuje?
CELKOVÉ ŘEŠENÍ
Vykreslíme popsanou situaci. V bodě A právě pozorovatel sleduje západ Slunce. Na idealizovaném rozhraní vakua a atmosféry dochází k lomu v bodě P.
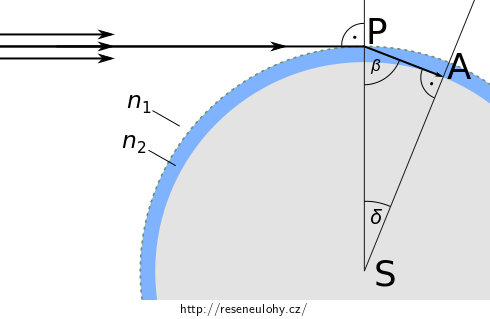
V mezním případě je úhel dopadu \(\alpha = \frac{\pi}{2}.\) Úhel lomu jsme označili \(\beta\).
Ze Snellova zákona lomu pro rozhraní vakuum-vzduch
\[ n_1 \sin\frac{\pi}{2} = n_2 \sin \beta \]vyjádříme úhel lomu
\[ \beta = \arcsin \frac{n_1}{n_2} . \tag{1}\]Pokud by neexistovalo rozhraní, nedošlo by k lomu a západ Slunce by pozorovatel sledoval již v okamžiku, kdy byl spolu se Zemí u bodu P. Od této doby se Země pootočila o úhel
\[\delta = \frac{\pi}{2} - \beta.\]Vyjádříme-li úhlovou rychlost \(\omega\) otáčení Země jako podíl plného úhlu \(2\pi\) a periody otáčení Země \(T\), můžeme pro hledaný čas psát
\[t = \frac{\delta}{\omega} = \frac{\frac{\pi}{2} - \beta}{\frac{2\pi}{T}}.\]Úpravou a dosazením za úhel \(\beta\) z (1) získáváme konečný vztah
\[ t = \frac{1}{2\pi} \left[\frac{\pi}{2} - \arcsin \left(\frac{n_1}{n_2} \right)\right]T. \]Dosazením číselných hodnot pak dostáváme
\[ t = \frac{1}{2\pi} \left[\frac{\pi}{2} - \arcsin \left(\frac{1}{1{,}0003} \right)\right]24{\cdot} 60~\mathrm{min} \doteq 5{,}6~\mathrm{min}. \]Komentář k řešení
V zadání příkladu je uveden požadavek na pravý úhel při bodu P, díky čemuž se příklad jednoduše počítá. Nicméně takové zjednodušení je přílišné a byť dává úloha velmi dobrý odhad zpoždění, je to výsledek velmi nereálného modelu – za takových podmínek totiž vychází tloušťka atmosféra necelé \(2\,\mathrm{km}\).
Reálně nedochází pouze k jednomu lomu, ale v důsledku průběžné změny indexu lomu k lomu v každém místě atmosféry a paprsek se ohýbá „hladčeji“.
Trajektorii postupně ohýbajícího se paprsku si můžete bez složitých výpočtu numericky napočítat např. v tabulkovém editoru (Excel, OpenOffice Calc,..)
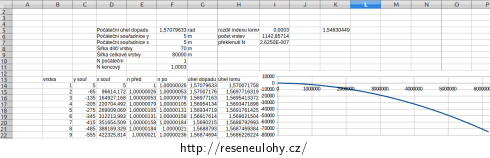
Počáteční a konečný index lomu, počáteční souřadnice, úhel dopadu, šířku a počet vrstev lze zanést jako parametry a zkoumat, jak se s nimi trajektorie paprsků mění.
Odpověď
Náš jednoduchý model dává výsledné zpoždění západu Slunce přibližně \(5{,}6\,\mathrm{min}\).


