Délka stínu nohou plameňáka
Úloha číslo: 1655
Plameňák stojí ve vodě tak, že celé jeho nohy o délce 60 cm jsou v ní ponořené.
Jak dlouhý stín vrhají jeho nohy na dno rybníku, jestliže index lomu vody je 1,33 a sluneční paprsky dopadají na vodní hladinu pod úhlem 60° (úhel od kolmice)?
Změní se délka stínu jeho nohou, kdyby stál na souši? Pokud ano, jak se změní?
Poznámka: Stín těla nebudeme uvažovat.
Zápis
\(h=60\) \(\mathrm{cm}=\) \(0{,}6\) \(\mathrm{m}\) délka nohou plameňáka \(n=\) \(1{,}33\) index lomu vody \(α=\) \(60\mathrm{°}\) úhel pod kterým dopadají sluneční paprsky na hladinu \(d_{v}=\) \(?\) délka stínu nohou ve vodě \(d_{s}=\) \(?\) délka stínu nohou na souši Nápověda 1
Uvědomte si, jak vzniká stín a na základě toho určete, jak dlouhý stín nohou bude mít plaměnák, který stojí na souši.
Nápověda 2
Podívejte se nyní na plameňáka, který stojí ve vodě. Co se stane s paprskem, když dopadne na hladinu vody? Ovlivní to, že jsou nohy ponořené ve vodě, délku jejich stínu?
Nápověda 3
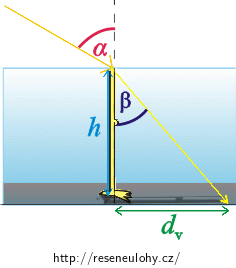
Zde je část obrázku (z řešení nápovědy 2), kterou potřebujeme pro řešení naší úlohy.
S pomocí Snellova zákona dopočítejte délku stínu \(d_{v}\).
Celkové řešení
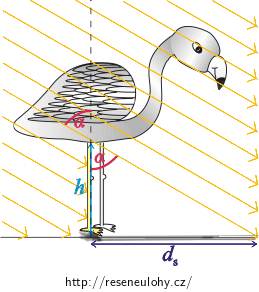
Plameňák na souši
Ze zadání víme, že sluneční paprsky dopadají k hladině vody pod úhlem 60°. Když bude plaměňák stát na souši, tak sluneční paprsky budou dopadat k zemi pod úhlem \(α=60°\).
Bude nám stačit podívat se na délku stínu jen u jedné nohy (stín těla a stín druhé nohy nebudeme uvažovat).
Stín bude začínat u nohy a končit bude v místě, na které dopadne první paprsek světla.
Z obrázku vidíme, že platí: \[\mathrm{tg}\, {α}=\frac{d_{s}}{h}.\]
Obě strany rovnice vynásobíme \(h\) a dostáváme délku stínu na souši: \[d_{s}=h\cdot \mathrm{tg}\, {α}.\]
Číselné řešení
\(h=\) \(60\) \(\mathrm{cm}=\) \(0{,}6\) \(\mathrm{cm}\)
\(α=\) \(60\mathrm{°}\)
Dosadíme:
\(d_{s}=\) \(0{,}6 \cdot \mathrm{tg}\, {60°}\) \(\mathrm{m}=0{,}6 \cdot \sqrt {3}\) \(\mathrm{m}\) \(\dot=\) \(1{,}04\) \(\mathrm{m}=\) \(104\) \(\mathrm{cm}.\)
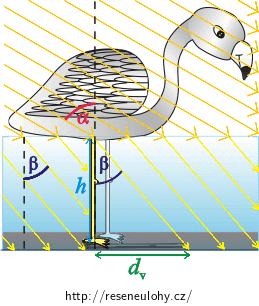
Plameňák ve vodě
Po dopadu paprsku na hladinu vody se jedna jeho část bude lámat pod úhlem \(β\) a druhá část se bude odrážet pod úhlem \(α \). Budeme se zabývat pouze částí paprsku, která se láme (protože odražená část paprsku délku stínu neovlivní). Napíšeme si Snellův zákon: \[\frac {\sin α}{\sin β}=\frac {n}{n_{0}},\] kde \(n_{0}\) je index lomu vzduchu a \(n\) je index lomu vody.
Obě strany rovnice vynásobíme \(n_{0}\sin β\) a vydělíme \(n\): \[\sin β= \frac {n_{0}\sin α}{n}.\tag{1}\]
Opět nám bude stačit podívat se na délku stínu jen u jedné nohy.
Podobně jako na souši, začátek stínu bude u nohy a konec stínu bude v místě, na které dopadne první paprsek světla.
Z obrázku vidíme, že platí: \[\sin {β}=\frac{d_{v}}{\sqrt{d_{v}^2+h^2}},\tag{2}\] kde \(\sqrt{d_{v}^2+h^2}\) je přepona trojúhelníku, jejiž velikost jsme určili z Pythagorovy věty.
Dosadíme ze vztahu (1) do vztahu (2) za \(\sin β\): \[\frac {n_{0}\sin α}{n}=\frac{d_{v}}{\sqrt{d_{v}^2+h^2}}\]
Chceme vyjádřit \(d_{v}\). Nejprve obě strany rovnice umocníme: \[\frac {n_{0}^2\sin^2 α}{n^2}=\frac{d_{v}^2}{d_{v}^2+h^2}.\]
Obě strany rovnice vynásobíme \(d_{v}^2+h^2\): \[d_{v}^2 \frac {n_{0}^2\sin^2 α}{n^2}+h^2\frac {n_{0}^2\sin^2 α}{n^2}=d_{v}^2.\] Převedeme členy s \(d_{v}^2\) na jednu stranu rovnice: \[\frac {h^2 n_{0}^2\sin^2 α}{n^2}=d_{v}^2 −\frac {d_{v}^2 n_{0}^2\sin^2 α}{n^2}.\] Vytkneme \(d_{v}^2\) a obě strany rovnice vydělíme \(\left(1−\frac {n_{0}^2\sin^2 α}{n^2}\right)\): \[\frac {h^2 n_{0}^2\sin^2 α}{n^2 \left(1−\frac {n_{0}^2\sin^2 α}{n^2}\right)}=d_{v}^2.\]
Převedeme členy v závorce na společného jmenovatele a vykrátíme \(n^2\): \[\frac {h^2 n_{0}^2\sin^2 α}{ n^2−n_{0}^2\sin^2 α}=d_{v}^2.\]
Obě strany rovnice odmocníme a dostáváme délku stínu: \[d_{v}=\frac {h n_{0}\sin α}{\sqrt{ n^2−n_{0}^2\sin^2 α}}.\]
Číselné řešení
Ze zadání víme:
\(h=\) \(60\) \(\mathrm{cm}=\) \(0{,}6\) \(\mathrm{m}\)
\(α=\) \(60\mathrm{°}\)
\(n=\) \(1{,}33\)
V tabulkách dohledáme hodnotu indexu lomu vzduchu \(n_{0}\):
\(n_{0}\) \(=\) \(1{,}00\)
Dosadíme:
\(d_{v}=\) \(\frac {0{,}6 {\cdot} 1 \cdot\sin 60°}{\sqrt{ 1{,}33^2−1^2 \cdot \sin^2 60°}}\) \(\mathrm{m}\) \(=\) \(\frac {0{,}6 \cdot \frac{\sqrt{3}}{2}}{\sqrt{ 1{,}33^2−\frac{3}{4}}}\) \(\mathrm{m}\) \(\dot=\) \(0{,}51\) \(\mathrm{m}\) \(=\) \(51\) \(\mathrm{cm}.\)
Délka stínu nohou na souši je \(d_{s}\) \(\dot=\) \(104\) \(\mathrm{cm}\) a ve vodě je \(d_{v}\) \(\dot=\) \(51\) \(\mathrm{cm}\). Tedy na souši by byl stín nohou \(\frac{d_{s}}{d_{v}}=\frac{104}{51}\dot=\) \(2{,}04\) krát delší než ve vodě.
Odpověď
Délka stínu nohou plameňáka na dně rybníku bude přibližně \(51\) \(\mathrm{cm}\).
Kdyby plameňák stál na souši, pak by délka stínu jeho nohou byla přibližně \(104\) \(\mathrm{cm}\) (byl by zhruba dvakrát delší).