Sbírka řešených úloh

Odraz světla ve skleněné podkově

Úloha číslo: 1830

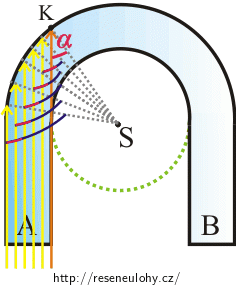
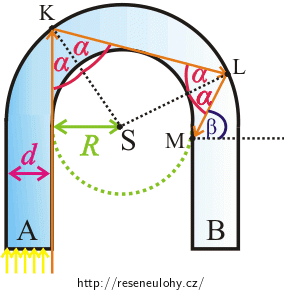
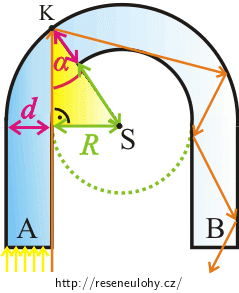
Skleněná tyč obdélníkového průřezu je ohnuta do tvaru „podkovy“ (viz obrázek). Vnitřní prohnutí podkovy je kruhové s poloměrem \(R\) a vnější prohnutí je také kruhové s poloměrem \(R+d\).

Svazek rovnoběžných paprsků světla dopadá kolmo na plochu A. Určete minimální hodnotu podílu \(\frac{R}{d}\), aby veškeré světlo z tohoto svazku opustilo skleněnou podkovu povrchem B.

• Nápověda 1

  Protože nechceme, aby některý z paprsků opustil podkovu v jiném místě než plochou B, musí v podkově docházet k tzv. totálnímu odrazu paprsků. Uvědomte si, kdy dochází k totálnímu odrazu paprsků a napište Snellův zákon pro totální odraz světla.

• Řešení nápovědy 1

  Totální odraz paprsků nastává ve chvíli, když nedochází k jejich lomu. Je třeba, aby světlo procházelo z opticky hustšího do opticky řidšího prostředí (bude tedy nastávat lom od kolmice). Maximální úhel dopadu, při kterém ještě nastává lom světla nazýváme mezní úhel \(α_{m}\) (pro úhel lomu platí \(β_{m}=90°\)).

  Aby nastal totální odraz, tak pro úhel dopadu paprsku \(α\) musí platit, že bude větší než mezní úhel \(α_{m}\): \[ α \gt α_{m}. \] Pokud je úhel dopadu menší než \(90°\) a zároveň platí \(α \gt α_{m}\), bude také platit: \[\sin{α} \gt \sin{α_{m}}.\tag{1}\] Snellův zákon pro totální odraz světla: \[\frac{\sin{α_{m}}}{\sin{90°}}=\frac{n_{2}}{n_{1}},\] kde \(n_{2}\) je index lomu opticky řidšího prostředí a \(n_{1}\) je index lomu opticky hustšího prostředí.

   

  Snellův zákon pro náš případ: \[\frac{\sin{α_{m}}}{\sin{90°}}=\frac{n_{v}}{n_{s}},\] kde \(n_{v}\) je index lomu vzduchu a \(n_{s}\) je index lomu skla, kterým se paprsky šíří.

  Protože platí \(\sin{90°}=1\) a dle tabulek \(n_{v}  \dot= 1\), můžeme napsat: \[\sin{α_{m}}=\frac{1}{n_{s}}.\] Tento vztah dosadíme do vztahu (1): \[\sin{α} \gt \frac{1}{n_{s}}.\tag{2}\]

• Nápověda 2

  Rozmyslete si, zda je potřeba zabývat se všemi paprsky ze svazku světla.

• Řešení nápovědy 2

  V obrázku označíme střed S našich dvou myšlených kružnic. Popišme si nyní chod paprsku, který je v obrázku vyznačen oranžovou barvou. Předpokládáme, že paprsek bude dopadat na vnější kružnici pod úhlem dopadu \(α\). Místo jeho dopadu (a následné místo odrazu) si označíme písmenem K.

  Pro další paprsky bude úhel dopadu na vnější kružnici vždy větší než \(α\). Z toho plyne, že pokud bude u oranžového paprsku docházet k totálnímu odrazu, bude také u všech dalších paprsků docházet k totálnímu odrazu a nemusíme se jimi už dále zabývat.

  

  Bude nám tedy stačit zabývat se pouze chodem krajního (oranžového) paprsku.

• Nápověda 3

  Nyní se budeme zabývat tím, jak se paprsek pohybuje v „zahnuté“ části podkovy.

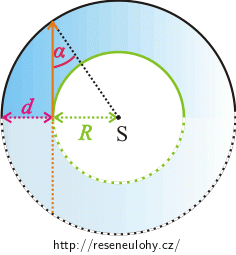
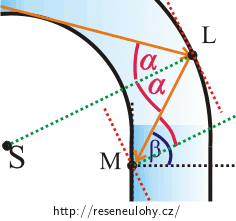
  Představte si dvě soustředné kružnice a mezi nimi skleněné mezikruží. Dále si představte paprsek, jehož trajektorie tvoří tečnu k „vnitřní“ kružnici a který dopadá na „vnější“ kružnici pod úhlem \(α\).

  

  Jak bude pokračovat trajektorie paprsku? Zakreslete ji do obrázku.

• Řešení nápovědy 3

  Paprsek se bude odrážet pod úhlem \(α\). Do obrázku si můžeme zakreslit pomyslný trojúhelník (žlutý), jehož jeden úhel bude úhlem dopadu. Zobrazíme-li tento trojúhelník v osové souměrnosti podle kolmice dopadu, dostaneme trojúhelník, jehož jeden úhel bude úhlem odrazu. Jelikož trajektorie dopadajícího paprsku tvoří tečnu k „vnitřní“ kružnici, tak z osové souměrnosti trojúhelníků plyne, že i trajektorie odraženého paprsku bude tečnou k „vnitřní“ kružnici.

  

  Paprsek tedy bude na vnější kružnici dopadat stále pod stejným úhlem \(α\). Dále bychom pokračovali analogicky.

  

  Vrátíme se k obrázku podkovy. Zjistili jsme, že trajektorie odraženého paprsku bude tečnou k „vnitřní“ kružnici. Paprsek bude v celém půlkruhovém mezikruží dopadat a odrážet se pod stejným úhlem.

  

• Poznámka

  Při jiném poměru \(\frac{R}{d}\) se paprsek v polokruhovém mezikruží může odrazit jednou nebo více než dvakrát. Nic se však nezmění na tom, že paprsek bude v tomto mezikruží dopadat a odrážet se pod stejným úhlem.

• Nápověda 4

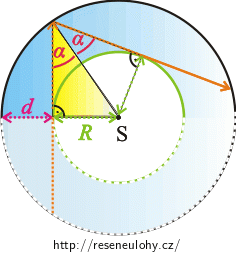
  Pod jakým úhlem dopadá paprsek do bodu M?

  

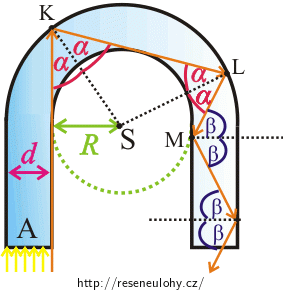
  Bude v tomto bodě docházet k totálnímu odrazu? Do obrázku zakreslete trajektorii paprsku ve zbylé části podkovy.

• Řešení nápovědy 4

  Paprsek dopadá do bodu M pod úhlem \( β\).

  

  Aby v bodě M docházelo k totálnímu odrazu, pak musí platit \( β \ge α \). Přesuneme-li kolmici dopadu z bodu L do bodu M (v obrázku je vyznačena zeleně), pak vidíme, že úhel \(β\) bude větší než úhel \( α\).

  

  Ve zbylé části podkovy bude paprsek dopadat a odrážet se pod úhlem \(β\).

  

• Nápověda 5

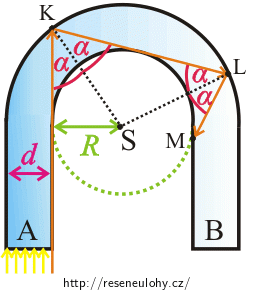
  Zjistili jsme, že když paprsek bude dopadat do bodu K pod úhlem \(α \gt α_{m}\), pak bude v celé podkově docházet k totálnímu odrazu do chvíle, než opustí podkovu plochou B.

  

  Pomocí obrázku určete, jaká je závislost mezi úhlem \(α\), poloměrem \(R\) a šířkou podkovy \(d\). Následně za pomoci vztahu (2) určete poměr \(\frac{R}{d}\).

• Řešení nápovědy 5

  Podíváme-li se pozorně na pravoúhlý trojúhelník v obrázku, pak zjistíme, že délka jeho přepony odpovídá součtu \(R+d\).

  

  Využijeme goniometrickou funkci sinus: \[\sin{α}=\frac{R}{R+d}.\tag{3}\] Připomeneme si vztah (2): \[\sin{α} \gt \frac{1}{n_{s}}.\] Spojením rovnic (2) a (3) zjistíme, že pokud chceme, aby v podkově docházelo k totálnímu odrazu, musí platit: \[\frac{R}{R+d}\gt \frac{1}{n_{s}} .\] Protože nás však zajímá limitní případ (kdy se úhel dopadu na vnější kružnici \(α\) rovná meznímu úhlu \(α_{m}\) a tedy i \(\sin{α}=\sin{α_{m}}\)), budeme dále tuto nerovnost zapisovat ve tvaru: \[\frac{R}{R+d}\ge \frac{1}{n_{s}} .\] Pro přehlednost si nerovnici přepíšeme: \[\frac{1}{n_{s}} \le \frac{R}{R+d}.\] Vynásobíme obě strany nerovnice kladným výrazem \(\frac{R+d}{R}\): \[\frac{1}{n_{s}}\frac{R+d}{R} \le 1.\] Budeme upravovat levou stranu nerovnice: \[\frac{1}{n_{s}}\left(\frac{R}{R}+\frac{d}{R} \right)\le 1,\] \[\frac{1}{n_{s}}\left(1+\frac{d}{R} \right)\le 1.\] Roznásobíme závorku: \[\frac{1}{n_{s}}+\frac{1}{n_{s}}\frac{d}{R} \le 1.\] Od obou stran nerovnice odečteme \(\frac{1}{n_{s}}\): \[\frac{1}{n_{s}}\frac{d}{R} \le 1 − \frac{1}{n_{s}}.\] Pravou stranu nerovnice převedeme na společného jmenovatele: \[\frac{1}{n_{s}}\frac{d}{R} \le \frac{n_{s}−1}{n_{s}}.\] Vynásobíme obě strany nerovnice \(n_{s}\): \[\frac{d}{R} \le n_{s}−1.\] Převrátíme zlomky: \[\frac{R}{d} \ge \frac{1}{ n_{s}−1}. \]

  Číselné řešení

  V tabulkách dohledáme hodnotu indexu lomu skla \(n_{s} = 1{,}5\) a dosadíme: \[\frac{R}{d} \ge \frac{1}{ 1{,}5−1}, \] \[\frac{R}{d} \ge 2. \]

• Celkové řešení

  Totální odraz

  Nechceme, aby některý z paprsků opustil podkovu v jiném místě než plochou B, proto musí v podkově docházet k tzv. totálnímu odrazu paprsků.

  Aby nastal totální odraz, tak pro úhel dopadu paprsku \(α\) musí platit, že bude větší než mezní úhel \(α_{m}\): \[ α \gt α_{m}. \] Pokud je úhel dopadu menší než \(90°\) a zároveň platí \(α \gt α_{m}\), bude také platit: \[\sin{α} \gt \sin{α_{m}}.\tag{1}\]

   

  Mezní úhel je takový úhel, při kterém ještě dochází k lomu paprsku. Paprsek se pak láme pod úhlem \(90°\). Pro tento případ zapíšeme Snellův zákon lomu jako:

  \[\frac{\sin{α_{m}}}{\sin{90°}}=\frac{n_{v}}{n_{s}},\]

  kde \(n_{v}\) je index lomu vzduchu a \(n_{s}\) je index lomu skla.

  Protože platí \(\sin{90°}=1\) a dle tabulek \(n_{v}  \dot= 1\), můžeme napsat: \[\sin{α_{m}}=\frac{1}{n_{s}}.\] Tento vztah dosadíme do vztahu (1): \[\sin{α} \gt \frac{1}{n_{s}}.\tag{2}\]

   

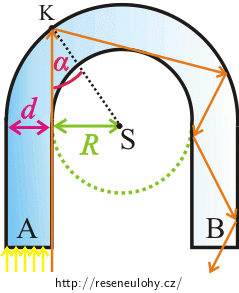
  Jeden paprsek stačí

  Není potřeba zabývat se všemi paprsky ze svazku světla. Bude nám stačit zaměřit se pouze na chod krajního (oranžového) paprsku. Pokud bude u oranžového paprsku docházet k totálnímu odrazu, bude také u všech dalších paprsků docházet k totálnímu odrazu (další paprsky budou dopadat na vnější kružnici pod větším úhlem než je úhel dopadu oranžového paprsku).

  

  Pokud tedy u oranžového paprsku bude docházet při prvním dopadu na rozhraní sklo-vzduch k totálnímu odrazu, bude k němu docházet i v celé podkově. Přesvědčit se o tom můžeme v Nápovědě 3 a Nápovědě 4.

   

  Minimální hodnota podílu \(\frac{R}{d}\)

  Podíváme-li se pozorně na pravoúhlý trojúhelník (žlutý) v obrázku, pak zjistíme, že délka jeho přepony odpovídá součtu \(R+d\).

  

  Využijeme goniometrickou funkci sinus: \[\sin{α}=\frac{R}{R+d}.\tag{3}\] Připomeneme si vztah (2) a dosadíme do něj: \[\sin{α} \gt \frac{1}{n_{s}}.\] \[\frac{R}{R+d}\gt \frac{1}{n_{s}} .\] Protože nás zajímá i limitní případ, tedy případ, kdy je úhel dopadu \(α\) roven meznímu úhlu \(α_{m}\) (a tedy i \(\sin{α}=\sin{α_{m}}\)), budeme dále pracovat s nerovností: \[\frac{R}{R+d}\ge \frac{1}{n_{s}} .\] Pro přehlednost si nerovnici přepíšeme: \[\frac{1}{n_{s}} \le \frac{R}{R+d}.\] Vynásobíme obě strany nerovnice kladným výrazem \(\frac{R+d}{R}\): \[\frac{1}{n_{s}}\frac{R+d}{R} \le 1.\] A upravujeme nerovnici tak, abychom na levé straně získali výraz \(\frac{R}{d}\): \[\frac{1}{n_{s}}\left(\frac{R}{R}+\frac{d}{R} \right)\le 1,\] \[\frac{1}{n_{s}}\left(1+\frac{d}{R} \right)\le 1,\] \[\frac{1}{n_{s}}+\frac{1}{n_{s}}\frac{d}{R} \le 1,\] \[\frac{1}{n_{s}}\frac{d}{R} \le 1 − \frac{1}{n_{s}},\] \[\frac{1}{n_{s}}\frac{d}{R} \le \frac{n_{s}−1}{n_{s}},\] \[\frac{d}{R} \le n_{s}−1,\] \[\frac{R}{d} \ge \frac{1}{ n_{s}−1}. \]

  Číselné řešení

  V tabulkách dohledáme hodnotu indexu lomu skla \(n_{s} = 1{,}5\) a dosadíme: \[\frac{R}{d} \ge \frac{1}{ 1{,}5−1}, \] \[\frac{R}{d} \ge 2. \]

• Odpověď

  Aby došlo v podkově k totálnímu odrazu, minimální hodnota podílu \(\frac{R}{d}\) musí být rovna dvěma.

• Odkaz na experiment

  Předvedení experimentu s totálním odrazem je popsáno v Totální odraz ve vytékající vodě.