Sbírka řešených úloh

Překryv optických spekter vyšších řádů

Úloha číslo: 1662

• Obrázek dvou sousedních spekter

  Takto by to vypadalo, pokud by se spektra nepřekrývala.

  

• Nápověda 1

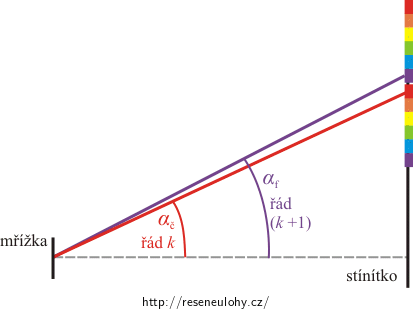
  To, zda se spektra překryjí nebo nepřekryjí, zaleží na tom, který z úhlů vyznačených na obrázku v předchozím oddíle je větší. Jak můžeme tyto úhly porovnat?

  Z kterého vztahu můžeme vypočítat úhel odchýlení pro krajní hodnoty viditelného světla za pomoci dráhového rozdílu Δl?

• Řešení nápovědy 1

  Úhel odchýlení na mřížce spočítáme ze vztahu:

  \[\mathrm{\Delta}l = \,b\sin\,\alpha \quad\Rightarrow\quad \sin\,\alpha=\,\frac{\mathrm{\Delta}l}{b},\]

  kde b je mřížková konstanta, Δl je dráhový rozdíl paprsků a α je úhel odchýlení.

  Pro podrobné vysvětlení se podívejte na úlohu Výpočet úhlu odchýlení maxima.

  Pro interferenční maximum platí vztah:

  \[\mathrm{\Delta}l=\,k\lambda\]

  kde λ je vlnová délka a k je řád maxima.

  Za λ si dosadíme vlnové délky červeného světla λ_č k-tého řádu a fialového světla λ_f řádu k+1.

  \[\sin\,\alpha_\mathrm{č}=\,\frac{k\lambda_\mathrm{č}}{b},\] \[\sin\,\alpha_\mathrm{f}=\,\frac{(k+1)\lambda_\mathrm{f}}{b}.\]

  Pro zjištění, zda se vyšší řády překrývají, potřebujeme zjistit, který z úhlů α_č a α_f je větší. Protože je funkce sinus na intervalu od \(0\) do \(\frac{\pi}{2}\) rostoucí, bude stejná nerovnost mezi úhly i mezi jejich siny.

• Řešení

  Takto by to vypadalo, pokud by se spektra nepřekrývala.

  

  Pro úhel odchýlení paprsků vytvářejících interferenční maximum platí:

  \[\mathrm{\Delta}l = \,b\sin\,\alpha \quad\Rightarrow\quad \sin\,\alpha=\,\frac{\mathrm{\Delta}l}{b} \quad\Rightarrow\quad \sin\,\alpha=\,\frac{k\lambda}{b},\]

  kde b je mřížková konstanta, Δl = kλ je dráhový rozdíl paprsků, α je úhel odchýlení a k je řád maxima.

  Napíšeme si rovnice pro odchýlení červeného světla v maximu k-tého řádu a fialového světla v maximu řádu k+1:

  \[\sin\,\alpha_\mathrm{č}=\,\frac{k\lambda_\mathrm{č}}{b},\] \[\sin\,\alpha_\mathrm{f}=\,\frac{(k+1)\lambda_\mathrm{f}}{b}.\]

  Pro zjištění, zda se vyšší řády překrývají, potřebujeme zjistit, který z úhlů α_č a α_f je větší. Protože je funkce sinus na intervalu od \(0\) do \(\frac{\pi}{2}\) rostoucí, bude stejná nerovnost mezi úhly i mezi jejich siny. Tj. naším úkolem je porovnat hodnoty výrazů

  \[k\lambda_\mathrm{č} \qquad \mathrm{a} \qquad (k+1)\lambda_\mathrm{f}.\]

   

  Dosadíme číselné hodnoty.

   

  1) Porovnání pro 1. a 2. řád:

  Tedy k = 1:

  \[1\,\cdot\,780 \gt 2\,\cdot\,350 \quad\Rightarrow\quad 780 \gt 700.\]

  Z této nerovnosti je zřejmé, že se 1. a 2. řád překryje.

  1) Porovnání pro 2. a 3. řád:

  Tedy k = 2:

  \[2\,\cdot \,780 \gt 3 \,\cdot \,350 \quad\Rightarrow\quad 1560 \gt 1050.\]

  Z této nerovnosti je zřejmé, že se 2. a 3. řád překryje.

  1) Porovnání pro 3. a 4. řád:

  Tedy k = 3:

  \[3 \,\cdot \, 780 \gt 4 \,\cdot\,350 \quad\Rightarrow\quad 2340 \gt 1400.\]

  Z této nerovnosti je zřejmé, že se i 3. a 4. řád překryje.

  

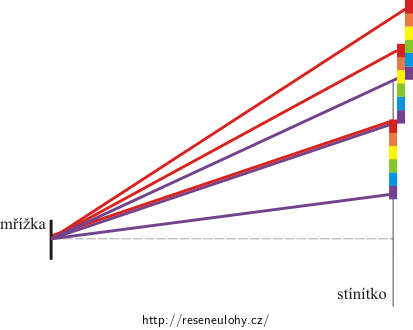
• Odpověď

  Ano, optická spektra vyšších řádů se navzájem překrývají.

• Komentář

  Úlohu bychom mohli řešit i jednodušeji, i když ne tak obecně. Úhly odchýlení bychom vypočítali numericky s nějakou námi zvolenou hodnotou mřížkové konstanty a poté je navzájem porovnali.