Sbírka řešených úloh

Správná velikost zrcadla

Úloha číslo: 1654

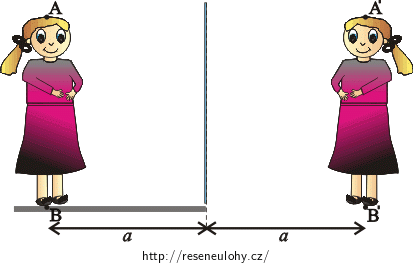
Jak vysoké musí být rovinné zrcadlo zavěšené svisle na stěnu, aby žena vysoká 160 cm stojící 1 m od zrcadla viděla v zrcadle celou svoji postavu? Její oči jsou ve svislé vzdálenosti 10 cm od temene hlavy.

V jaké výšce od podlahy musí být dolní okraj zrcadla?

Bude třeba změnit velikost zrcadla, aby žena viděla celou svoji postavu z větší vzdálenosti?

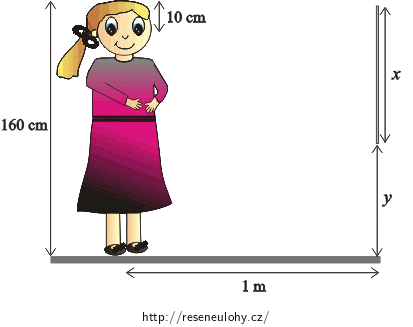
• Zápis

  \(h=160\) \(\mathrm{cm}=\) \(1{,}6\) \(\mathrm{m}\)	výška ženy
  \(a=1\) \(\mathrm{m}=\) \(1{,}0\) \(\mathrm{m}\)	vzdálenost ženy od zrcadla
  \(o=10\) \(\mathrm{cm}=\) \(0{,}1\) \(\mathrm{m}\)	vzdálenost očí od temene hlavy
  \(x=\) \(?\)	výška zrcadla
  \(y=\) \(?\)	vzdálenost dolního okraje zrcadla od podlahy

• Nápověda 1

  Díky tomu, že známe vlastnosti obrazu vytvořeného rovinným zrcadlem, můžeme nakreslit, jak bude vypadat obraz ženy. Do obrázku si přidáme krajní body A a B, které se zobrazí na A' a B'.

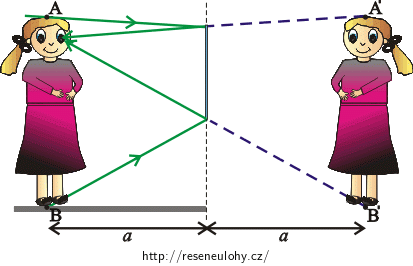
  Nakreslete paprsek jdoucí bodem A a paprsek jdoucí bodem B tak, aby se paprsky odrazily do očí ženy.

  

• Řešení nápovědy 1

  Nakreslíme paprsek jdoucí bodem A tak, aby po odrazu od zrcadla dopadl do očí ženy. Když protáhneme odražený paprsek za zrcadlo, tak projde bodem A'. Oči potom vidí bod A'.

  Hledáme zrcadlo o nejmenší možné výšce (ve kterém uvidíme bod A' i B'), proto potřebujeme, aby se paprsek jdoucí bodem A odrážel od horního okraje zrcadla.

  Podobně budeme postupovat pro paprsek jdoucí bodem B. Chceme, aby se tento paprsek odrážel od dolního okraje zrcadla

  

  Žena vidí body A' a B'. Z toho plyne, že vidí celou svoji postavu.

• Nápověda 2

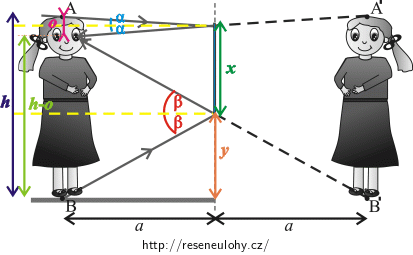
  Zákon odrazu nám říká, že úhel dopadu se rovná úhlu odrazu (toho jsme využili při kreslení odražených paprsků). Na obrázku dopadá paprsek z temena hlavy na zrcadlo pod úhlem \(α\) a odráží se do očí také pod úhlem \(α\). Když paprsek dopadá na zrcadlo pod úhlem \(β\), tak se odráží pod úhlem \(β\).

  Do obrázku si zakreslíme úhly \(α, β\) a všechny důležité vzdálenosti (které známe nebo které chceme určit).

  

  S pomocí obrázku a znalostí z geometrie určete výšku zrcadla \(x\) a vzdálenost dolního okraje zrcadla od podlahy \(y\).

  Jak závisí velikost zrcadla na vzdálenosti ženy od zrcadla?

• Řešení nápovědy 2

  Uvědomíme si:

  • kolmice dopadu pro paprsek jdoucí bodem A půlí \(o\).
  • kolmice dopadu pro paprsek procházejícím bodem B půlí \(h−o\).

  Tyto dvě informace doplníme do obrázku.

  

  Pro lepší přehlednost překreslíme obrázek bez ženy a jejího obrazu.

  

  Z obrázku vidíme, že pro výšku zrcadla bude platit: \[x=\frac{o}{2}+\frac{h-o}{2}=\frac{h}{2}.\]

  Z tohoto vztahu vyplývá, že velikost zrcadla nezávisí na vzdálenosti ženy od zrcadla.

  Z obrázku také určíme vzdálenost dolního okraje zrcadla od podlahy: \[y=\frac{h−o}{2}.\]

  Číselné řešení:

  Ze zadání víme:

  \(h=\) \(1{,}6\) \(\mathrm{m}\)

  \(o=\) \(0{,}1\) \(\mathrm{m}\)

  Po dosazení dostáváme:

  \(x=\) \(\frac{1{,}6}{2} \mathrm{m}\) \(=\) \(0{,}8\) \(\mathrm{m}\) \(=\) \(80\) \(\mathrm{cm}\),

  \(y=\) \(\frac{1{,}6−0{,}1}{2} \mathrm{m}\) \(=\) \(0{,}75\) \(\mathrm{m}\) \(=\) \(75\) \(\mathrm{cm}\).

• Celkové řešení

  Obraz ženy a hledané zrcadlo

  Díky tomu, že známe vlastnosti obrazu vytvořeného rovinným zrcadlem, můžeme nakreslit, jak bude vypadat obraz ženy. Do obrázku si přidáme krajní body A a B, které se zobrazí na A' a B'.

  Nakreslíme paprsek jdoucí bodem A tak, aby po odrazu od zrcadla dopadl do očí ženy. Když protáhneme odražený paprsek za zrcadlo, tak projde bodem A'. Oči potom vidí bod A'.

  Hledáme zrcadlo o nejmenší možné výšce (ve kterém uvidíme bod A' i B'), proto potřebujeme, aby se paprsek jdoucí bodem A odrážel od horního okraje zrcadla.

  Podobně budeme postupovat pro paprsek jdoucí bodem B. Chceme, aby se tento paprsek odrážel od dolního okraje zrcadla

  

  Žena vidí body A' a B'. Z toho plyne, že vidí celou svoji postavu.

   

  Výška a umístění zrcadla kvantitativně

  Zákon odrazu nám říká, že úhel dopadu se rovná úhlu odrazu (toho jsme využili při kreslení odražených paprsků). Na obrázku dopadá paprsek pod úhlem \(α\) a odráží se také pod úhlem \(α\). Když dopadá pod úhlem \(β\), tak se odráží pod úhlem \(β\).

  Uvědomíme si:

  • kolmice dopadu pro paprsek jdoucí bodem A půlí \(o\).
  • kolmice dopadu pro paprsek procházejícím bodem B půlí \(h−o\).

  Tyto dvě informace doplníme do obrázku.

  

  Pro lepší přehlednost překreslíme obrázek bez ženy a jejího obrazu.

  

  Z obrázku vidíme, že pro výšku zrcadla bude platit: \[x=\frac{o}{2}+\frac{h-o}{2}=\frac{h}{2}.\]

  Z tohoto vztahu vyplývá, že velikost zrcadla nezávisí na vzdálenosti ženy od zrcadla.

  Z obrázku také určíme vzdálenost dolního okraje zrcadla od podlahy: \[y=\frac{h−o}{2}.\]

  Číselné řešení:

  Ze zadání víme:

  \(h=\) \(1{,}6\) \(\mathrm{m}\)

  \(o=\) \(0{,}1\) \(\mathrm{m}\)

  Po dosazení dostáváme:

  \(x=\) \(\frac{1{,}6}{2} \mathrm{m}\) \(=\) \(0{,}8\) \(\mathrm{m}\) \(=\) \(80\) \(\mathrm{cm}\),

  \(y=\) \(\frac{1{,}6−0{,}1}{2} \mathrm{m}\) \(=\) \(0{,}75\) \(\mathrm{m}\) \(=\) \(75\) \(\mathrm{cm}\).

• Odpověď

  Zrcadlo musí být vysoké 80 cm a jeho dolní okraj musí být ve výšce 75 cm od podlahy. Pokud se žena postaví do jiné vzdálenosti od zrcadla, velikost zrcadla nebude třeba měnit.

• Úloha k procvičení

  Zkuste si rozmyslet, jak by se situace změnila, kdyby před zrcadlem stál chlapec o výšce 120 cm, který by měl na hlavě vysoký klobouk (výška klobouku nad temenem hlavy je 40 cm). Oči chlapce jsou ve svislé vzdálenosti 10 cm od temene hlavy.

• Řešení úlohy k procvičení

  Ze zadání úlohy:

  \(h=\)  \(1{,}2\) \(\mathrm{m}\) \(+\) \(0{,}4\) \(\mathrm{m}=\) \(1{,}6\) \(\mathrm{m}\),

  \(o= \)  \(0{,}4\) \(\mathrm{m}\) \(+\) \(0{,}1\) \(\mathrm{m}=\)  \(0{,}5\) \(\mathrm{m}\).

  Výška zrcadla: \(x=\frac{h}{2}.\)

  Vzdálenost dolního okraje zrcadla od podlahy: \(y=\frac{h−o}{2}.\)

  Po dosazení dostáváme:

  \(x=\) \(\frac{1{,}6}{2} \mathrm{m}\) \(=\) \(80\) \(\mathrm{cm}\),

  \(y=\) \(\frac{1{,}6−0{,}5}{2} \mathrm{m}\) \(=\) \(55\) \(\mathrm{cm}\).

  Zrcadlo bude stejně vysoké jako v původní úloze, ale bude umístěno v jiné výšce (dolní okraj zrcadla bude ve výšce \(55\) \(\mathrm{cm}\)) od podlahy.