Sbírka řešených úloh

Obraz Slunce vytvořený pomocí Keplerova dalekohledu

Úloha číslo: 1741

Keplerův dalekohled má objektiv o ohniskové vzdálenosti \(1 \mathrm{m}\). Okulár má ohniskovou vzdálenost \(5 \mathrm{cm}\). Projekční stínítko, na němž lze projekcí vytvořit obraz Slunce, je od okuláru vzdáleno \(25 \mathrm{cm} \). Určete vzdálenost mezi objektivem a okulárem a průměr obrazu Slunce, když víme, že Slunce bychom pozorovali pod zorným úhlem \(30\mathrm{′}\).

• Zápis

  \(f_{1}= 1 \mathrm{m}\)	ohnisková vzdálenost objektivu
  \(f_{2}=5 \mathrm{cm}= 5{\cdot}10^{−2}  \mathrm{m}\)	ohnisková vzdálenost okuláru
  \(a'_{2}=25 \mathrm{cm}= 25{\cdot}10^{−2}  \mathrm{m}\)	vzdálenost stínítka od okuláru
  \(τ=30\mathrm{′}\)	zorný úhel
  \(l= ?\)	vzdálenost mezi objektivem a okulárem
  \(d= ?\)	průměr obrazu Slunce, který se vytvoří na stínítku

• Nápověda 1

  Z čeho se Keplerův dalekohled skládá? Jak funguje?

• Řešení nápovědy 1

  Keplerův dalekohled se skládá ze dvou spojných čoček. První se nazývá „objektiv“, a má poměrně velkou ohniskovou vzdálenost. Druhá se nazývá „okulár“, a její ohnisková vzdálenost je podstatně menší.

  

  Popis obrázku

  \(F_{1}\)	předmětové ohnisko objektivu
  \(F'_{1}\)	obrazové ohnisko objektivu
  \(F_{2}\)	předmětové ohnisko okuláru
  \(F'_{2}\)	obrazové ohnisko okuláru
  \(τ\)	zorný úhel
  \(τ'\)	zvětšený zorný úhel

  Na obrázku je schéma Keplerova dalekohledu v případě, že jím pozorujeme velmi vzdálený předmět. Velká vzdálenost předmětu způsobuje, že na objektiv dopadá svazek rovnoběžných paprsků a v obrazovém ohnisku objektivu vzniká zmenšený, převrácený a skutečný obraz. Okulár pak funguje jako lupa.

• Nápověda 2

  V jakém místě vytvoří objektiv obraz Slunce? Nakreslete si obrázek Slunce, objektivu a obrazu Slunce vytvořeného objektivem.

• Řešení nápovědy 2

  Do objektivu budou dopadat paprsky pod zorným úhlem \(τ\). Do našeho obrázku už nebudeme kreslit svazek paprsků, který dopadá na objektiv. Pro vyřešení úlohy nám bude stačit zabývat se jen tím paprskem, který prochází středem objektivu.

  

  Popis obrázku

  \(F_{1}\)	předmětové ohnisko objektivu
  \(F'_{1}\)	obrazové ohnisko objektivu
  \(τ\)	zorný úhel
  \(a_{1}\)	předmětová vzdálenost objektivu
  \(a'_{1}\)	obrazová vzdálenost objektivu
  \(y\)	výška předmětu (Slunce)
  \(y'\)	výška obrazu Slunce vytvořeného objektivem

  Předmět (Slunce) je ve velké vzdálenosti od objektivu \(a_{1}\), proto obraz Slunce vytvořený objektivem vznikne v ohnisku objektivu.

  Bude platit: \(a'_{1}=f_{1}\), kde \(a'_{1}\) je vzdálenost obrazu od objektivu a \(f_{1}\) je ohnisková vzdálenost objektivu.

• Jak víme, že pro velmi vzdálené předměty platí a'₁=f₁?

  Využijeme zobrazovací rovnice pro objektiv: \[\frac{1}{a_{1}}+\frac{1}{a'_{1}}=\frac{1}{f_{1}}.\] Pro velmi vzdálené předměty se hodnota členu \(\frac{1}{a_{1}}\) blíží nule (dělíme jedničku velkým číslem), proto ho můžeme zanedbat. Dostáváme: \[\frac{1}{a'_{1}}=\frac{1}{f_{1}}.\] A odtud plyne: \[a'_{1}=f_{1}.\]

• Nápověda 3

  Chceme, aby za okulárem vznikl skutečný obraz ve vzdálenosti \(a'_{2}\) od okuláru. V jakém místě musí být umístěn okulár? Do obrázku “Zobrazení obrazu Slunce objektivem” z řešení nápovědy 2 dokreslete okulár a obraz Slunce vytvořeného okulárem.

• Řešení nápovědy 3

  

  Popis dokreslené části obrázku

  \(τ'\)	zvětšený zorný úhel
  \(a_{2}\)	předmětová vzdálenost okuláru
  \(a'_{2}\)	obrazová vzdálenost okuláru (vzdálenost okuláru od stínítka)
  \(y''=d\)	výška obrazu Slunce vytvořeného okulárem
  \(l\)	vzdálenost mezi objektivem a okulárem

  Zatím nejsme schopni říci, jaká je vzdálenost okuláru od objektivu \(l\). Z toho důvodu nejsou v obrázku zakreslena ohniska okuláru \(F_{2}\), \(F'_{2}\). Jejich umístění zjistíme až ve chvíli, kdy budeme znát vzdálenost \(l\).

• Nápověda 4

  Pomocí zobrazovací rovnice pro okulár určete vzdálenost obrazu vytvořeného objektivem od okuláru \(a_{2}\). Určete hodnotu vzdálenosti mezi objektivem a okulárem \(l\).

• Řešení nápovědy 4

  Využijeme zobrazovací rovnice pro okulár: \[\frac{1}{a_{2}}+\frac{1}{a'_{2}}=\frac{1}{f_{2}}.\]

  Od obou stran rovnice odečteme \(\frac{1}{a'_{2}}\): \[\frac{1}{a_{2}}=\frac{1}{f_{2}}−\frac{1}{a'_{2}}.\]

  Zlomky na pravé straně rovnice převedeme na společného jmenovatele: \[\frac{1}{a_{2}}=\frac{a'_{2}−f_{2}}{a'_{2}f_{2}}.\]

  Vyjádříme \(a_{2}\): \[ a_{2}=\frac{a'_{2}f_{2}}{a'_{2}−f_{2}}.\tag{1}\]

  Pro vzdálenost mezi objektivem a okulárem \(l\) platí: \[l=f_{1}+a_{2}.\] Dle (1) dosadíme za \(a_{2}\): \[l=f_{1}+\frac{a'_{2}f_{2}}{a'_{2}−f_{2}}.\]

  Číselné řešení Ze zadání víme: \(f_{1}= 1 \mathrm{m}\) \(f_{2}=5{\cdot}10^{−2}  \mathrm{m}\) \(a'_{2}=25{\cdot}10^{−2}  \mathrm{m}\) Dosadíme: \(l=\left(1 +\frac{25{\cdot}10^{−2}\cdot 5{\cdot}10^{−2}}{25{\cdot}10^{−2}−5{\cdot}10^{−2}}\right)  \mathrm{m}\) \(l \dot= 1{,}06 \mathrm{m}\)

  Z řešení vyplývá, že ohnisko okuláru \(F_{2}\) je \(1 \mathrm{cm}\) za obrazem \(y'\) (viz obrázek).

• Nápověda 5

  Užitím goniometrických funkcí si vyjádřete úhly \(τ\) a \(τ'\).

• Řešení nápovědy 5

  

  Dle obrázku: \[ \mathrm{tg}\,{τ}=\frac{y'}{f_{1}}, \tag{2}\] \[ \mathrm{tg}\,{τ'}=\frac{y'}{a_{2}}=\frac{d}{a'_{2}}. \tag{3}\]

• Nápověda 6

  Využitím vztahů (1), (2) a (3) určete hodnotu průměru \(d\), tedy průměr obrazu Slunce.

• Řešení nápovědy 6

  \[ a_{2}=\frac{a'_{2}f_{2}}{a'_{2}−f_{2}}.\tag{1}\] \[ \mathrm{tg}\,{τ}=\frac{y'}{f_{1}}, \tag{2}\] \[ \mathrm{tg}\,{τ'}=\frac{y'}{a_{2}}=\frac{d}{a'_{2}}. \tag{3}\]

  Vyjádříme \(d\) ze vztahu (3): \[ \frac{y'}{a_{2}}=\frac{d}{a'_{2}}.\] Obě strany rovnice vynásobíme \(a'_{2}\) a prohodíme levou a pravou stranu rovnice: \[ d=a'_{2}\frac{y'}{a_{2}}.\tag{4}\] Obě strany rovnice (2) vynásobíme \(f_{1}\) a prohodíme levou a pravou stranu rovnice: \[ y'=f_{1}\mathrm{tg}\,{τ}. \tag{5}\] Do vztahu (4) dosadíme dle vztahů (1) a (5) a výraz upravíme: \[ d=a'_{2}\frac{f_{1}\mathrm{tg}\,{τ}}{\frac{a'_{2}f_{2}}{a'_{2}−f_{2}}}=\frac{f_{1}\mathrm{tg}\,{τ}}{\frac{f_{2}}{a'_{2}−f_{2}}}=f_{1}\mathrm{tg}\,{τ}\frac{a'_{2}−f_{2}}{f_{2}} .\]

  Číselné řešení

  Ze zadání víme:

  \(f_{1}= 1 \mathrm{m}\)

  \(f_{2}=5{\cdot}10^{−2}  \mathrm{m}\)

  \(a'_{2}=25{\cdot}10^{−2}  \mathrm{m}\)

  \(τ=30\mathrm{′}\)

  Dosadíme:

  \(d=1\cdot\mathrm{tg}\,{30\mathrm{′}}\frac{25{\cdot}10^{−2}−5{\cdot}10^{−2}}{5{\cdot}10^{−2}} \mathrm{m} \dot= 3{,}5{\cdot}10^{−2} \mathrm{m}=3{,}5 \mathrm{cm}.\)

• Celkové řešení

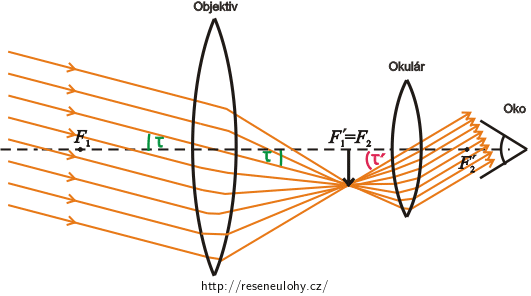
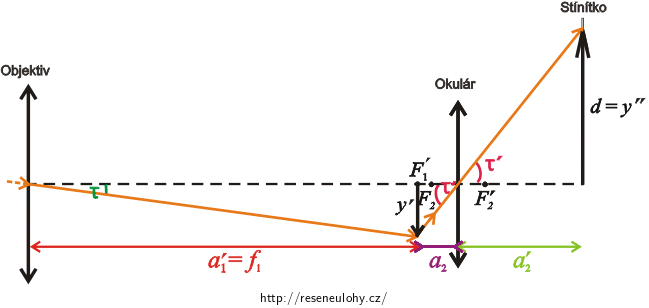
  Obrázek našeho dalekohledu

  Keplerův dalekohled se skládá ze dvou spojných čoček (objektiv a okulár).

  Do objektivu budou dopadat paprsky pod zorným úhlem \(τ\). Pro vyřešení úlohy nám bude stačit zabývat se jen tím paprskem, který prochází středem objektivu.

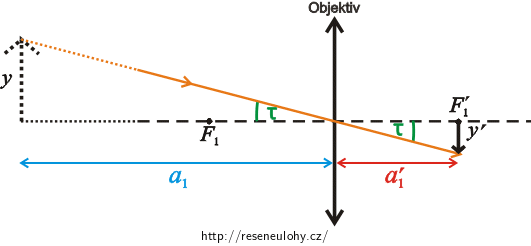
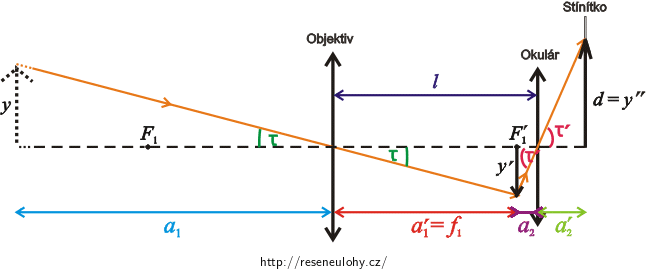
  Nakreslíme si obrázek Slunce, objektivu a obrazu Slunce vytvořeného objektivem. Dále do obrázku přidáme okulár a obraz Slunce vytvořeného okulárem.

  

  Popis obrázku

  \(F_{1}\)	předmětové ohnisko objektivu
  \(F'_{1}\)	obrazové ohnisko objektivu
  \(τ\)	zorný úhel
  \(τ'\)	zvětšený zorný úhel
  \(a_{1}\)	předmětová vzdálenost objektivu
  \(a'_{1}\)	obrazová vzdálenost objektivu
  \( \)
  \(a_{2}\)	předmětová vzdálenost okuláru
  \(a'_{2}\)	obrazová vzdálenost okuláru (vzdálenost okuláru od stínítka)
  \(l\)	vzdálenost mezi objektivem a okulárem
  \(y\)	výška předmětu (Slunce)
  \(y'\)	výška obrazu Slunce vytvořeného objektivem
  \(y''=d\)	výška obrazu Slunce vytvořeného okulárem

   

  Slunce je ve velké vzdálenosti od objektivu \(a_{1}\), proto obraz Slunce vytvořený objektivem vznikne v ohnisku objektivu.Bude tedy platit: \(a'_{1}=f_{1}\), kde \(f_{1}\) je ohnisková vzdálenost objektivu.

  Zatím nejsme schopni říci, jak daleko je okulár od objektivu \(l\). Z toho důvodu nejsou v obrázku zakreslena ohniska okuláru \(F_{2}\), \(F'_{2}\).

   

  Vzdálenost mezi objektivem a okulárem \(l\)

  Pomocí zobrazovací rovnice pro okulár určíme vzdálenost obrazu vytvořeného objektivem od okuláru \(a_{2}\): \[\frac{1}{a_{2}}+\frac{1}{a'_{2}}=\frac{1}{f_{2}}.\]

  Od obou stran rovnice odečteme \(\frac{1}{a'_{2}}\): \[\frac{1}{a_{2}}=\frac{1}{f_{2}}−\frac{1}{a'_{2}}.\]

  Zlomky na pravé straně rovnice převedeme na společného jmenovatele: \[\frac{1}{a_{2}}=\frac{a'_{2}−f_{2}}{a'_{2}f_{2}}.\]

  Vyjádříme \(a_{2}\): \[ a_{2}=\frac{a'_{2}f_{2}}{a'_{2}−f_{2}}.\tag{1}\]

  Pro vzdálenost mezi objektivem a okulárem \(l\) platí: \[l=a'_{1}+a_{2}=f_{1}+a_{2}.\] Dle (1) dosadíme za \(a_{2}\): \[l=f_{1}+\frac{a'_{2}f_{2}}{a'_{2}−f_{2}}.\]

  Číselné řešení Ze zadání víme: \(f_{1}= 1 \mathrm{m}\) \(f_{2}=5{\cdot}10^{−2}  \mathrm{m}\) \(a'_{2}=25{\cdot}10^{−2}  \mathrm{m}\) Dosadíme: \(l=\left(1 +\frac{25{\cdot}10^{−2}\cdot 5{\cdot}10^{−2}}{25{\cdot}10^{−2}−5{\cdot}10^{−2}}\right)  \mathrm{m} \dot= 1{,}06 \mathrm{m}\)

  Z řešení vyplývá, že ohnisko okuláru \(F_{2}\) je \(1 \mathrm{cm}\) za obrazem \(y'\).

   

  Průměr obrazu Slunce \(d\)

  

  Užitím goniometrických funkcí si vyjádříme úhly \(τ\) a \(τ'\): \[ \mathrm{tg}\,{τ}=\frac{y'}{f_{1}}, \tag{2}\] \[ \mathrm{tg}\,{τ'}=\frac{y'}{a_{2}}=\frac{d}{a'_{2}}. \tag{3}\]

  Vyjádříme \(d\) ze vztahu (3): \[ \frac{y'}{a_{2}}=\frac{d}{a'_{2}}.\] Obě strany rovnice vynásobíme \(a'_{2}\) a prohodíme levou a pravou stranu rovnice: \[ d=a'_{2}\frac{y'}{a_{2}}.\tag{4}\] Obě strany rovnice (2) vynásobíme \(f_{1}\) a prohodíme levou a pravou stranu rovnice: \[ y'=f_{1}\mathrm{tg}\,{τ}. \tag{5}\] Do vztahu (4) dosadíme dle vztahů (1) (za \(a_{2}\)) a (5) (za \(y'\)) a výraz upravíme: \[ d=a'_{2}\frac{f_{1}\mathrm{tg}\,{τ}}{\frac{a'_{2}f_{2}}{a'_{2}−f_{2}}}=\frac{f_{1}\mathrm{tg}\,{τ}}{\frac{f_{2}}{a'_{2}−f_{2}}}=f_{1}\mathrm{tg}\,{τ}\frac{a'_{2}−f_{2}}{f_{2}} .\]

  Číselné řešení

  Ze zadání víme:

  \(f_{1}= 1 \mathrm{m}\)

  \(f_{2}=5{\cdot}10^{−2}  \mathrm{m}\)

  \(a'_{2}=25{\cdot}10^{−2}  \mathrm{m}\)

  \(τ=30\mathrm{′}\)

  Dosadíme:

  \(d=1\cdot\mathrm{tg}\,{30\mathrm{′}}\frac{25{\cdot}10^{−2}−5{\cdot}10^{−2}}{5{\cdot}10^{−2}} \mathrm{m} \dot= 3{,}5{\cdot}10^{−2} \mathrm{m}=3{,}5 \mathrm{cm}.\)

• Odpověď

  Vzdálenost mezi objektivem a okulárem je \(1 \mathrm{m}\) a \(6 \mathrm{cm}\).

  Průměr obrazu Slunce vytvořeného na stínítku je \(3{,}5 \mathrm{cm}\).

• Jak se bude lišit nastavení dalekohledu pro oko a pro zobrazování na stínítko?

  Obvykle se do Keplerova dalekohledu díváme okem a chceme, aby okulár poslal do oka rovnoběžné paprsky a na sítnici se pak vytvořil obraz. Pokud se díváme do okuláru zdravým okem (bez optické vady), pak obraz vytvořený objektivem umístíme do ohniska okuláru. V tomto případě obrazové ohnisko objektivu a předmětové ohnisko okuláru budou na stejném místě.

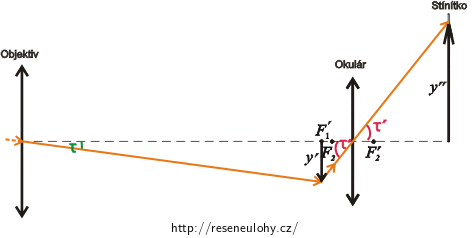
  V naší úloze však chceme, aby okulár vytvořil obraz na stínítku, které má od okuláru určitou vzdálenost. Aby v této vzdálenosti vznikl obraz, který nebude rozmazaný, tak potřebujeme vzdálenost mezi objektivem a okulárem upravit. V našem případě jsme zjistili, že musíme předmětové ohnisko okuláru umístit o centimetr dál od obrazového ohniska objektivu.