Sbírka řešených úloh

Výpočet úhlu odchýlení maxima

Úloha číslo: 1646

• Nápověda 1

  Co je to mřížková konstanta?

• Řešení nápovědy 1

  Mřížková konstanta je vzdálenost dvou sousedních štěrbin mřížky.

  

• Nápověda 2

  Zjistěte dráhový rozdíl paprsků procházejících sousedními otvory mřížky.

• Řešení nápovědy 2

  Nejdříve si nakreslíme situaci, jak prochází monochromatické světlo v tomto případě idealizovanou mřížkou o pěti vrypech. Nakreslíme všechny paprsky, které dopadají do bodu P na stínítku.

  

  Z obrázku si vezmeme dva sousední paprsky a nakreslíme si je zblízka.

  Předpokládáme, že naše stínítko je tak daleko od mřížky, že paprsky přicházející do určitého bodu P stínítka jsou přesto přibližně rovnoběžné.

  

  Z pravoúhlého trojúhelníku v obrázku dostaneme vztah:

  \[\mathrm{Δ}l = \,b\sin\,α,\]

  kde Δl je dráhový rozdíl dvou sousedních paprsků, b je mřížková konstanta a α je úhel, který paprsky svírají s centrální osou.

  V bodě P může vzniknout interferenční maximum nebo minimum, záleží na velikosti dráhového rozdílu sousedních paprsků.

• Nápověda 3

  Jaký vztah platí pro interferenční maxima?

• Řešení nápovědy 3

  Paprsky v bodě P se mají složit do světlého proužku, tedy do maxima. Pro interferenční maximum platí vztah:

  \[\mathrm{Δ}l = k λ,\]

  kde λ je vlnová délka a k je řád maxima a platí, že k = 0, 1, 2, 3, ...

  V naší úloze máme počítat s prvním maximem, tedy k = 1.

• Zápis

  b = 10−2 mm = 10−5 m	mřížková konstanta
  λ = 500 nm = 5,0·10−7 m	vlnová délka dopadajícího světla
  k = 1	řád maxima
  α = ? (°)	úhel odchýlení od kolmého směru

• Řešení

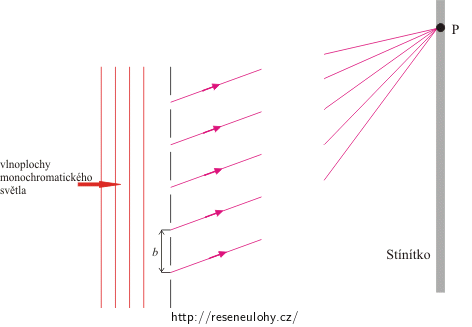
  Prochází-li monochromatické světlo mřížkou, dochází k ohybu světla na jednotlivých štěrbinách mřížky a na stínítku se vytvoří interferenční obrazec. Na stínítku vznikají interferenční maxima a minima, jejich poloha záleží na dráhovém rozdílu paprsků vycházejících ze sousedních štěrbin mřížky.

  Předpokládejme, že stínítko je tak daleko od mřížky, že paprsky přicházející do určitého bodu P stínítka jsou přibližně rovnoběžné.

  

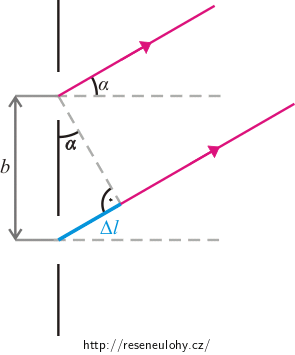
  Z pravoúhlého trojúhelníku na obrázku dostaneme vztah:

  \[\mathrm{Δ}l = \,b\sin\,α,\]

  kde Δl je dráhový rozdíl dvou sousedních paprsků, b je mřížková konstanta, tedy vzdálenost dvou štěrbin, a α je úhel, který paprsky svírají s centrální osou.

  Vyjádříme si úhel α a dostaneme:

  \[α= \,\arcsin\, \frac{\mathrm{Δ}l}{b}.\]

   

  Protože se paprsky v bodě P složily do světlého proužku, tedy do maxima, platí pro dráhový rozdíl Δl:

  \[\mathrm{Δ}l = k λ,\]

  a za k dosadíme první maximum, které máme v zadání, tedy k = 1.

  Dosadíme jednu rovnici do druhé a dosadíme číselné hodnoty, získáme:

  \[α= \,\arcsin \,\frac{λ}{b}=\,\arcsin \,\frac{5{,}0{\cdot}10^{−7}}{1{\cdot}10^{−5}}=\,2°52'.\]

• Odpověď

  Maximum prvního řádu se odchyluje o 2°51′ od směru kolmého k rovině mřížky.