DVD jako mřížka
Úloha číslo: 1661
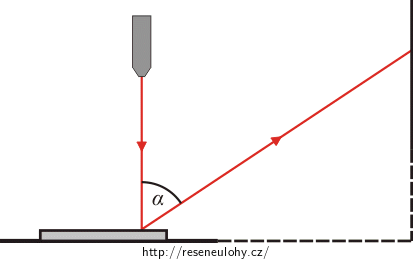
Emil, Evžen a Eva ve školním laboratorním cvičením z fyziky položili DVD na vodorovnou plochu a kolmo jej osvětlili světlem laserového ukazovátka o vlnové délce 650 nm. Na stěně ve vzdálenosti 130 cm se pak ve výšce 70 cm objevila stopa maxima prvního řádu. Uspořádání měření je na obrázku.
a) Jaká jim vyšla vzdálenost dvou sousedních záznamových stop na DVD?
b) Kolik záznamových stop se vedle sebe vejde na 1 mm délky?
Nápověda 1
DVD se chová jako mřížka. Proto si připomeňte: jaký vztah platí pro dráhový rozdíl paprsků?
Nápověda 2
Určete úhel odchýlení α prvního maxima pomocí zadaných vzdáleností.
Zápis
d = 130 cm = 1,3 m vzdálenost DVD od zdi k = 1 řád maxima λ = 650 nm = 6,5·10−7 m vlnová délka světla x = 70 cm = 0,7 m výška, ve které vzniklo maximum 1. řádu b = ? (nm) vzdálenost dvou stop N = ? počet stop na 1 mm délky Řešení
V této úloze se DVD chová jako mřížka, od které se světlo odráží. Tato mřížka se chová téměř stejně jako mřížka, kterou světlo prochází. Rozdíl je pouze v tom, že se ohybové jevy objeví na stejné straně mřížky, kde je i světelný zdroj.
V úloze chceme spočítat vzdálenost dvou stop a kolik stop se vejde na 1 mm délky. Pro tento výpočet se nám bude hodit najít vztah pro úhel odchýlení α a znát vztah pro dráhový rozdíl paprsků Δl.
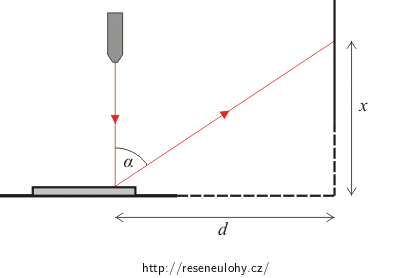
Z obrázku získáme vztah:
\[\mathrm{tg}\,\,α=\,\frac{d}{x},\]kde d je vzdálenost DVD od stěny a x je výška, ve které vzniklo maximum 1. řádu.
Pro dráhový rozdíl Δl platí:
\[\mathrm{Δ}l = \,b\sin\,α,\]kde Δl je dráhový rozdíl paprsků, b je vzdálenost dvou stop na DVD a α je úhel odchýlení.
Za Δl dosadíme podmínku pro maxima Δl = kλ, kde k = 1.
Vyjádříme si vzdálenost b:
\[b=\,\frac{\mathrm{Δ}l}{\sin\,α}=\,\frac{λ}{\sin\,α}.\]Číselné dosazení
Nejprve si vypočítáme úhel pomocí rovnice:
\[\mathrm{tg}\,\,α=\,\frac{d}{x}=\,\frac{1{,}3}{0{,}7}\,\dot=\,1{,}86 \quad\Rightarrow\quad α\,\dot=\,61{,}74°\]a poté vypočítáme vzdálenost dvou stop b:
\[b=\,\frac{6{,}5{\cdot}10^{−7}}{\sin\,61{,}74}\,\mathrm{m}\,\dot=\,7{,}40{\cdot}10^{−7}\,\mathrm{m}\,\dot=\,740\,\mathrm{nm}.\]Počet stop N na 1 mm získáme pomocí vztahu:
\[N=\,\frac{10^{−3}\,\mathrm{m}}{b}=\,\frac{10^{−3}\,\mathrm{m}}{7{,}38{\cdot}10^{−7}}\,\dot=\,1400.\]Odpověď
Vzdálenost dvou stop je na DVD 740 nm a na 1 mm se vedle sebe vejde 1400 stop.
Odkaz na pokus
Detailní popis toho, jak experiment s DVD provést, naleznete v pokusu Difrakce monochromatického světla na kompaktním disku.




