Optický hranol a zrcadlo
Úloha číslo: 1898
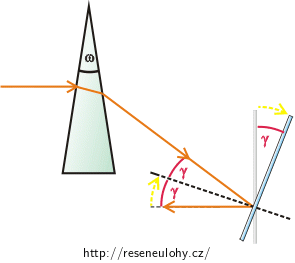
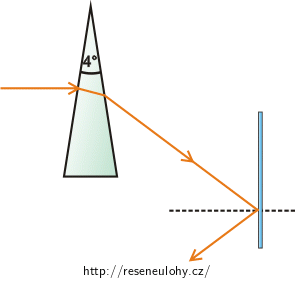
Paprsek světla dopadá horizontálně na optický hranol. Index lomu hranolu je 1,5 a jeho lámavý úhel je 4°. Následně paprsek prochází skrz tento hranol a dopadá na zrcadlo, které je ve vertikální poloze. Od zrcadla se paprsek odráží (viz obrázek).
Zápis
\(ω=4\mathrm{°}\) lámavý úhel \(n=1{,}5\) index lomu hranolu \(γ= ?\) úhel otočení zcadla Nápověda 1
Překreslete si obrázek ze zadání. Paprsek, který se odrazí od zrcadla nakreslete horizontálně. Rozmyslete si, jakým způsobem je třeba otočit zrcadlo, aby se paprsek odrazil tímto způsobem. Do obrázku vyznačte úhel otočení \(γ\).
Nápověda 2
Co znamená v optice pojem „deviace“? Jaký je vztah mezi deviací \(δ\) a úhlem otočení zrcadla \(γ\)?
Nápověda 3
Potřebujeme určit deviaci \(δ\). Jaký je vztah mezi deviací \(δ\) a lámavým úhlem \(ω\)?
Nápověda 4
Napište zákon lomu pro obě rozhraní (vzduch-hranol a hranol-vzduch).
Nápověda 5
Na základě toho, že lámavý úhel \(ω\) je velmi malý, můžeme zjednodušit zákon lomu pro obě rozhraní.
Nápověda 6
Celkové řešení
Vztah mezi úhlem otočení \(γ\) a deviací \(δ\)
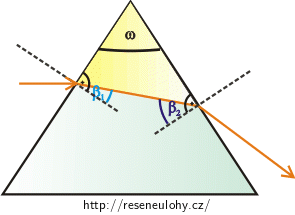
Překreslíme si obrázek ze zadání. Paprsek odražený od zrcadla nakreslíme horizontálně. Zrcadlo musíme otočit tak, aby platil zákon odrazu. Zrcadlo budeme otáčet kolem bodu dopadu paprsku. Protože tímto bodem prochází i kolmice dopadu, vyznačíme si do obrázku, jak se při otočení změní poloha zrcadla i této kolmice. Kolmice dopadu svírá se zrcadlem stále konstantní úhel, a tudíž její pootočení o úhel \(γ\) znamená, že se zrcadlo také otočí o úhel \(γ\).
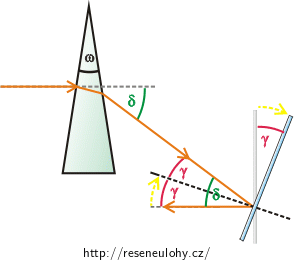
Dále jsme do obrázku vyznačili tzv. „deviaci“ \(δ\) (úhel, o který je vychýlen světelný paprsek po výstupu z hranolu od svého původního směru) Vztah mezi deviací \(δ\) a úhlem otočení zrcadla \(γ\) plyne z geometrie (využijeme tzv. střídavých úhlů): \[δ=2γ.\tag{1}\]
Vztah mezi deviací \(δ\) a lámavým úhlem \(ω\)
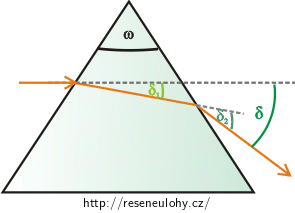
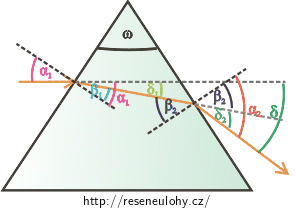
Postupně určíme vztah mezi deviací \(δ\) a lámavým úhlem \(ω\). Pro deviaci bude platit: \[δ=δ_{1}+δ_{2},\tag{2}\] kde \(δ_{1}\) je úhel, o který je po vstupu do hranolu vychýlen světelný paprsek a \(δ_{2}\) je úhel, o který je po výstupu z hranolu vychýlen světelný paprsek oproti paprsku, který procházel vnitřní částí hranolu.
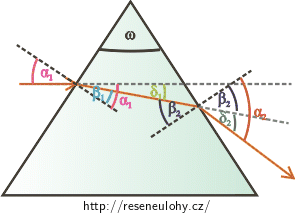
Pro \(δ_{1}\) platí: \[δ_{1}=α_{1}−β_{1},\tag{3}\] kde \(α_{1}\) je úhel dopadu paprsku na rozhraní vzduch-hranol a \(β_{1}\) je úhel lomu paprsku po vstupu do hranolu. Analogicky pro \(δ_{2}\) platí: \[δ_{2}=α_{2}−β_{2},\tag{4}\] kde \(β_{2}\) je úhel dopadu paprsku na rozhraní hranol-vzduch a \(α_{2}\) je úhel lomu paprsku po výstupu z hranolu.Protože součet všech úhlů ve vyznačeném žlutém trojúhelníku je \(180\mathrm{°}\), bude platit: \[ω+\left(90\mathrm{°}−β_{1}\right)+\left(90\mathrm{°}−β_{2}\right)= 180\mathrm{°}\] Po úpravě rovnice dostáváme: \[ω=β_{1}+β_{2}.\tag{5}\] Vztah (3) a (4) dosadíme do vztahu (2): \[δ=δ_{1}+δ_{2},\] \[δ=α_{1}−β_{1}+α_{2}−β_{2}.\] Upravíme: \[δ=α_{1}+α_{2}−\left(β_{1}+β_{2}\right).\] A dle (5) dostáváme vztah mezi \(δ\) a \(ω\) : \[δ=α_{1}+α_{2}−ω.\tag{6}\]Zákon lomu a jeho zjednodušení
Zákon lomu pro rozhraní vzduch-hranol: \[n_{vz}\sin{α_{1}}=n\sin{β_{1}},\tag{7}\] kde \(n\) je index lomu hranolu a \(n_{vz}\) je index lomu vzduchu.
Zákon lomu pro rozhraní hranol-vzduch: \[n_{vz}\sin{α_{2}}=n\sin{β_{2}}.\tag{8}\]
Uvědomíme si, že lámavý úhel \(ω\) je velmi malý a díky tomu jsou malé i úhly \(α_{1}\), \(α_{2}\), \(β_{1}\) a \(β_{2}\). Měříme-li úhly v radiánech, pak se hodnota sinu malého úhlu přibližně rovná velikosti tohoto úhlu, proto můžeme vztahy (7) a (8) přepsat následovně: \[n_{vz}α_{1}=nβ_{1},\tag{9}\] \[n_{vz}α_{2}=nβ_{2}.\tag{10}\]
Hledání úhlu otočení zrcadla \(γ\)
Ze zadání známe pouze hodnotu lámavého úhlu \(ω\) a index lomu hranolu \(n\). Index lomu vzduchu \(n_{vz}\) můžeme najít v tabulkách. Chceme, aby úhel \(γ\) byl závislý pouze na nám známých veličinách. Dle (9) a (10) vyjádříme úhly \(α_{1}\), \(α_{2}\): \[α_{1}=\frac{n}{n_{vz}}β_{1},\tag{11}\] \[α_{2}=\frac{n}{n_{vz}}β_{2}.\tag{12}\]
Nejprve si vyjádříme deviaci \(δ\).
Vztahy (11) a (12) dosadíme do vztahu (6): \[δ=\frac{n}{n_{vz}}β_{1}+\frac{n}{n_{vz}}β_{2}−ω.\] Vytkneme \(\frac{n}{n_{vz}}\): \[δ=\frac{n}{n_{vz}}\left(β_{1}+β_{2}\right)−ω.\] Za výraz \(β_{1}+β_{2}\) dosadíme dle (5) : \[δ=\frac{n}{n_{vz}}ω−ω.\] Vytkneme \(ω\): \[δ=ω\left(\frac{n}{n_{vz}}−1\right).\] Dosadíme do rovnice dle vztahu (1): \[2γ=ω\left(\frac{n}{n_{vz}}−1\right).\] Vydělíme obě strany rovnice \(2\): \[γ=\frac{ω}{2}\left(\frac{n}{n_{vz}}−1\right).\]
Číselné řešení
Ze zadání víme:
\(ω= 4\mathrm{°}\)
\(n= 1{,}5\)
V tabulkách můžeme dohledat:
\(n_{vz}= 1\)
Dosadíme:
\(γ=\frac{ω}{2}\left(\frac{n}{n_{vz}}−1\right)=\frac{4\mathrm{°}}{2}\left(\frac{1{,}5}{1}−1\right)= 1\mathrm{°}.\)
Odpověď
Zrcadlo musíme otočit o \(1 \mathrm{°}\) ve směru hodinových ručiček.
Úloha k procvičení
Jak by se situace změnila, kdybychom hranol ponořili do vody?
Odkaz na experiment
V Lom monochromatického světla optickým hranolem naleznete experiment, kterým se dá ukázat, kdy je deviace minimální.