Ohyb na dvojité štěrbině alternativně
Úloha číslo: 1525
Stanovte průběh intenzity světla na stínítku při Youngově interferenčním pokusu. Vzdálenost obou štěrbin šířky \(d\) je \(b\). Stínítko je umístěno ve vzdálenosti \(l\)
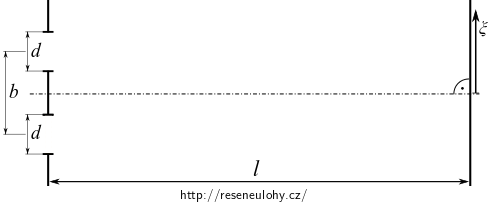
- Do výpočtu zahrňte vliv ohybového jevu na štěrbinách nezanedbatelné šířky.
- Na štěrbiny dopadá kolmo rovinná harmonická vlna, lineárně polarizovaná ve směru štěrbin.
- Řešte v aproximaci Fraunhoferova obybu.
Dvojštěrbinu chápejte jako dvě samostatné štěrbiny nezanedbatelné šířky, které jsou umístěný vedle sebe a z nich vycházející vlny spolu interferují. Ohyb na štěrbině jsme popisovali zde.
Rozbor
Pro výpočet budeme potřebovat průběh elektrické intenzity na stínítku při osvětlování jedné štěrbiny umístěné v ose
\[E(\alpha) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}, \qquad \mathrm{kde\,} \psi = k\frac{d}{2}\sin\alpha.\tag{1}\]V úloze s jednou štěrbinou byla tato štěrbina umístěna v ose experimentu. V naší situaci bude jedna ze štěrbin nad a druhá pod touto osou, čímž bude intenzita od jedné štěrbiny fázově předbíhat a od druhé fázově zaostávat oproti intenzitě jedné štěrbiny ležící v ose popsané vztahem (1).
Nápověda 1 – elektrické intenzity posunutých štěrbin
Průběh elektrické intenzity štěrbiny, která by byla v ose (naznačená zeleně), umíme popsat funkcí
\[ E(\alpha) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}, \qquad \mathrm{kde\,} \psi = k\frac{d}{2}\sin\alpha. \]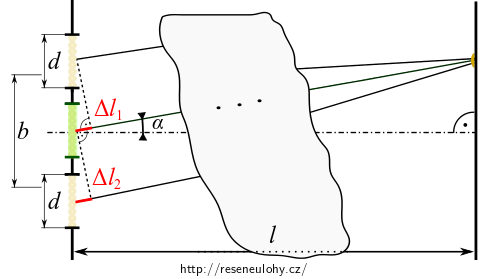
Napište vztah pro elektrickou intenzitu vlny vycházející ze štěrbiny do určitého směru vůči kolmici ke stínítku, potom přepište pro štěrbiny posunuté o \(b/2\) rovnoběžně se stínítkem tak, že díky vztahu \(L \gg b+d\) se budou vlny lišit jen o fázový posun, který lze určit v aproximaci rovnoběžných paprsků.
Nápověda 2 – superpozice elektrických intenzit
Výsledná elektrická intenzita v daném místě stínítka je superpozicí intenzit od obou štěrbin. Nalezněte výslednou elektrickou intenzitu jako součet intenzit \(E_1(\psi), E_2(\psi)\) a výraz upravte.
Nápověda 3 – průběh intenzity na stínítku
Ve velké vzdálenosti od štěrbiny lze části válcových vln považovat za rovinné a intenzitu světla tak lze vypočítat pomocí vztahu
\[ I = \frac{1}{2z_0} E_v E_v^\star. \]CELKOVÉ ŘEŠENÍ
Pro výpočet budeme potřebovat průběh elektrické intenzity na stínítku při osvětlování jedné štěrbiny umístěné v ose
\[E(\alpha) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}, \qquad \mathrm{kde\,} \psi = k\frac{d}{2}\sin\alpha.\tag{1}\]V úloze s jednou štěrbinou byla tato štěrbina umístěna v ose experimentu. V naší situaci bude jedna ze štěrbin nad a druhá pod touto osou, čímž bude intenzita od jedné štěrbiny fázově předbíhat a od druhé fázově zaostávat oproti intenzitě jedné štěrbiny ležící v ose popsané vztahem (1).
Průběh elektrické intenzity zelené štěrbiny v ose stínítka umíme popsat funkcí
\[ E(\alpha) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}, \qquad \mathrm{kde\,} \psi = k\frac{d}{2}\sin\alpha. \]
Zelená štěrbina je v obrázku zakreslena pouze pro odvození.
- Je-li štěrbina posunuta o \(\frac{b}{2}\) nahoru, bude dráha paprsku o \(\Delta l_1\) kratší. Elektrickou intenzitu zelené štěrbiny tak bude \(E_1(\alpha)\) fázově předbíhat. \[ \varphi_1 = -\omega \tau_1 = - kc\tau_1 = -k\Delta l_1\]
- Je-li štěrbina posunuta o \(\frac{b}{2}\) dolů, bude dráha paprsku o \(\Delta l_2\) delší. Vzhledem k elektrické intenzitě zelené štěrbiny tak bude \(E_2(\alpha)\) fázově opožděna. \[\varphi_2 = \omega \tau_2 = kc\tau_2 = k\Delta l_2\]
Fázový rozdíl \(\varphi\) se projeví znásobením průběhu komplexní exponenciálou \(e^{-i\varphi}\).
Průběhy elektrických intenzit od první a druhé štěrbiny tedy jsou
\[ \begin{eqnarray} E_1(\alpha) &=& E(\psi) e^{-i\varphi_1} = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}e^{ik\Delta l_1},\\ E_2(\alpha) &=& E(\psi) e^{-i\varphi_2} = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}e^{-ik\Delta l_2}. \end{eqnarray} \] Neboť \[ \Delta l_1 = \Delta l_2 = \frac{b}{2} \sin \alpha, \] máme \[ \begin{eqnarray} E_1(\alpha) &=& \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}e^{ik\frac{b}{2}\sin \alpha},\\ E_2(\alpha) &=& \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}e^{-ik\frac{b}{2}\sin \alpha}. \end{eqnarray} \]Výslednou elektrickou intenzitu získáme součtem intenzit \(E_1(\alpha), E_2(\alpha)\)
\[E_v(\alpha) = E_1(\alpha) + E_2(\alpha) = \] \[=\frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi} \left(e^{ik\frac{b}{2}\sin \alpha} + e^{-ik\frac{b}{2}\sin \alpha} \right).\]Zaveďme \(\phi = k\frac{b}{2}\sin \alpha\).
Samostatně upravíme závorku s komplexními exponenciálami. \[ \small e^{ik\frac{b}{2}\sin \alpha} + e^{-ik\frac{b}{2}\sin \alpha}= e^{i\phi} + e^{-i\phi} = \] \[ \small = \cos \phi + i\sin \phi + \cos( -\phi) + i\sin (-\phi) = 2\cos\phi. \]
Máme tedy
\[ \begin{array}{ll} E_v(\alpha) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi} 2\cos\phi, \qquad \mathrm{kde\,} & \psi = k\frac{d}{2} \sin\alpha,\\ & \phi = k\frac{b}{2} \sin\alpha. \end{array} \]Průběh intenzity světla získáme dosazením \(E_v(\alpha)\) a jejího komplexního sdružení do vztahu pro intenzitu
\[ I = \frac{1}{2z_0} E_v E_v^\star= \overbrace{\frac{2E_0^2 d^2}{z_0l}}^{\mathrm{ozn.\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi. \]Průběh intenzity je tedy
\[ \begin{array}{cl} I = I_0 \color{green}{\frac{\sin^2 \psi}{\psi^2}}\color{blue}{\cos^2 \phi}, \qquad \mathrm{kde}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha. \end{array} \]Vidíme, že průběh je součinem dvou funkcí:
- \(\color{green}{\frac{\sin^2 \psi}{\psi^2}}\), kterou jsme vypočítali v příkladě pro ohyb na štěrbině,
- \(\color{blue}{\cos^2 \phi}\), kterou jsme vypočítali v příkladě s interferencí na dvojštěrbině.
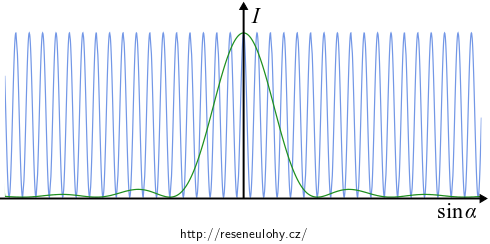
Součinem obou zakreslených funkcí dostáváme průběh intenzity na následujícím obrázku.
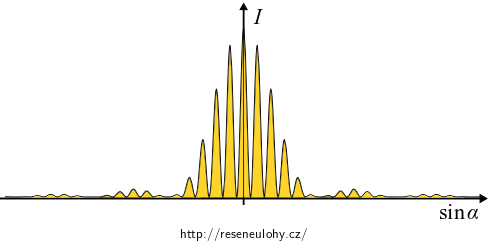
Odpověď
Průběh intenzity na stínítku je
\[ \begin{array}{cl} I = I_0 \frac{\sin^2 \psi}{\psi^2}\cos^2 \phi, \qquad \mathrm{kde}\quad & \psi = k\frac{d}{2}\sin \alpha, \\ & \phi = k\frac{b}{2}\sin \alpha, \\ & I_0 = \frac{2E_0^2 d^2}{z_0l}. \end{array} \]
Odkaz – Youngův pokus s ohybem integrací
Úloha lze řešit bez znalosti ohybu na jedné štěrbině přímou integrací, viz Ohyb na dvojité štěrbině.


