Sbírka řešených úloh

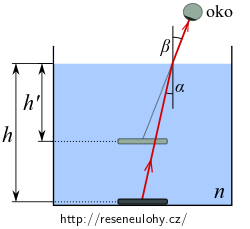
Index lomu kapaliny a mince

Úloha číslo: 1560

Na dno sklenice s průhlednou kapalinou výšky \(h\) jsme umístili minci.

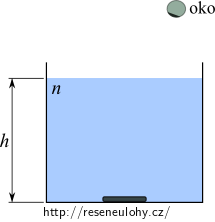
Budeme-li minci pozorovat mírně z boku, bude se v důsledku lomu světla na rozhraní kapalina-vzduch jevit, že se „vznáší“ v hloubce \(h^\prime\) pod hladinou. Zakreslete polohu okem pozorovaného obrazu a určete index lomu \(n\) kapaliny, jestliže minci pozorujme pod malými úhly.

• Nápověda 1 – obraz mince

  Nalezněte obraz mince, tj. nakreslete, kde minci uvidíme.

  Paprsky, které se odrážejí od daného bodu mince a dopadají na rozhraní, se na něm lámou a některé z nich dopadnou do oka. Z těchto paprsků zakreslete alespoň dva. Na prodloužení těchto paprsků pak leží obraz, který vidí naše oko.

• Řešení nápovědy 1 – obraz mince

  Chceme zjistit, kde bude oko minci pozorovat. Postačí, když se budeme zabývat pouze jejím středem. Na následujícím obrázku jsme nakreslili dva paprsky podobného směru (červeně), které se lámou na rozhraní a dopadají do oka.

  

  Oko si přicházející paprsky „prodlouží“ a střed mince budeme vidět na průsečíku těchto prodloužených (modrých) paprsků.

  Výsledkem je, že minci, která leží na dně, budeme pozorovat výše, v hloubce \(h^\prime\) pod hladinou.

• Nápověda 2 – zákon lomu

  Pro některý z paprsků, který docestuje z mince do oka, napište zákon lomu.

• Řešení nápovědy 2 – zákon lomu

  Úhly dopadu a lomu paprsků, které jsme vybrali v minulé části úlohy, se téměř neliší. Pro zákon lomu vybereme jeden z paprsků.

  

  Úhel dopadu jsme označili \(\alpha\), úhel lomu \(\beta\).

  Uvážíme-li, že index lomu okolního vzduchu je příbližně \(1\), píšeme zákon lomu ve tvaru

  \[ \frac{\sin \alpha}{\sin\beta} = \frac{1}{n}. \tag{1}\]

• Nápověda 3 – aproximace pro malé úhly

  Uvažujte, že minci pozorujeme pod malými úhly. Vyjádřete goniometrické funkce v zákonu lomu pomocí zadaných geometrických rozměrů \(h, h^\prime\).

• Řešení nápovědy 3 – aproximace pro malé úhly

  Je-li pozorovací úhel \(\beta\) malý, tj. \(\beta \ll 1\), je malý i úhel \(\alpha\), neboť \(\alpha \lt \beta\). Tedy

  \[ \sin \alpha \approx \tan \alpha, \] \[ \sin \beta \approx \tan \beta, \]

  

  a tedy dosazením do (1)

  \[\frac{\tan\alpha}{\tan\beta} \approx \frac{1}{n}.\tag{2}\]

  Z naznačených pravoúhlých trojúhelníků vyplývá, že

  \[\tan \alpha = \frac{s}{h},\] \[\tan \beta = \frac{s}{h^\prime}.\]

  Dosazením těchto vyjádření do (2) máme

  \[ \frac{\frac{s}{h}}{\frac{s}{h^\prime}} = \frac{h^\prime}{h} \approx \frac{1}{n}. \]

  Odtud snadno (rovnost pro malé pozorovací úhly)

  \[ n = \frac{h}{h^\prime}. \]

• CELKOVÉ ŘEŠENÍ

  Chceme zjistit, kde bude oko minci pozorovat. Na následujícím obrázku jsme nakreslili dva paprsky podobného směru (červeně), které se lámou na rozhraní a dopadají do oka. Oko si tyto přicházející paprsky „prodlouží“ a střed mince uvidíme ve zdánlivé hloubce \(h^\prime\)

  

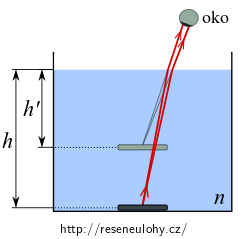
  Pro výpočet indexu lomu kapaliny použijeme zákon lomu, pro který vybereme jeden z paprsků.

  Úhel dopadu označíme jako \(\alpha\), úhel lomu \(\beta\).

  

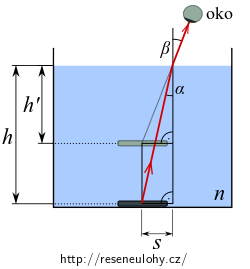
  Index lomu vzduchu je příbližně \(1\), píšeme zákon lomu ve tvaru

  \[ \frac{\sin \alpha}{\sin\beta} = \frac{1}{n}. \]

  Je-li pozorovací úhel \(\beta\) malý, tj. \(\beta \ll 1\), je malý i úhel \(\alpha\), neboť \(\alpha \lt \beta\). Tedy pro malé úhly platí

  \[ \sin \alpha \approx \tan \alpha, \] \[ \sin \beta \approx \tan \beta, \]

  a tedy dosazením do Snellova vzorce dostáváme

  \[\frac{\tan\alpha}{\tan\beta} \approx \frac{1}{n}.\]

  Z naznačených pravoúhlých trojúhelníků vyplývá, že

  \[\tan \alpha = \frac{s}{h},\] \[\tan \beta = \frac{s}{h^\prime}.\]

  Dosazením dostáváme

  \[ \frac{\frac{s}{h}}{\frac{s}{h^\prime}} = \frac{h^\prime}{h} \approx \frac{1}{n}. \]

  Odtud snadno (rovnost pro malé pozorovací úhly)

  \[ n = \frac{h}{h^\prime}. \]

• Odpověď

  Index lomu kapaliny, uvážíme-li index lomu vzduchu \(1\), je

  \[ n = \frac{h}{h^\prime}. \]

• Poznámka

  Pro vodu je \(h:h^\prime \doteq 4:3\), což dává index lomu přibližně \(n\doteq 1{,}3\). Experimentálně ověřte!