Mládě žirafy a kulové zrcadlo

Úloha číslo: 1742

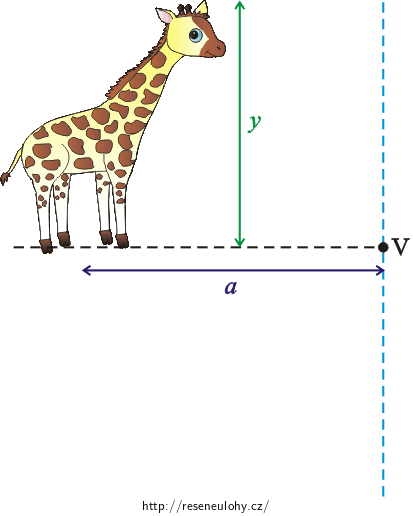
Představme si mládě žirafy, které má výšku \(2 \mathrm{m}\) a stojí \(1{,}5 \mathrm{m}\) před vrcholem kulového zrcadla. Zrcadlo vytváří obraz o výšce \(1 \mathrm{m}\). Určete poloměr křivosti a typ zrcadla.

Obrázek k zadání

Zápis

\(y= 2 \mathrm{m}\)	výška mláděte žirafy
\(\|y'\|=1 \mathrm{m}\)	výška obrazu mláděte žirafy
\(a=1{,}5 \mathrm{m}\)	vzdálenost mláděte žirafy od vrcholu kulového zrcadla
\(r= ?\)	poloměr křivosti kulového zrcadla

Znaménková konvence
V úloze používáme znaménkovou konvenci popsanou v Zobrazení netopýra kulovým zrcadlem a spojnou čočkou.
Nápověda 1
Jaký je vztah mezi ohniskem kulového zrcadla a jeho poloměrem?

Napište si zobrazovací rovnici pro kulové zrcadlo a vyjádřete odtud ohniskovou vzdálenost.
Řešení nápovědy 1
Pro poloměr kulového zrcadla (dutého i vypuklého) platí vztah: \[r=2f,\tag{1}\] kde \(f\) je ohnisková vzdálenost zrcadla. Napíšeme zobrazovací rovnici pro kulové zrcadlo: \[\frac{1}{a}+\frac{1}{a'}=\frac{1}{f},\] kde \(a\) je vzdálenost mláděte žirafy od vrcholu kulového zrcadla a \(a'\) je vzdálenost obrazu mláděte žirafy od vrcholu kulového zrcadla.

Zlomky na levé straně rovnice převedeme na společného jmenovatele: \[\frac{a+a'}{a\cdot a'}=\frac{1}{f}.\]

Vyjádříme \(f\): \[f=\frac{a\cdot a'}{a+a'} \tag{2}\]
Nápověda 2
Využitím vztahů pro zvětšení zrcadla určete vzdálenost obrazu mláděte žirafy od vrcholu zrcadla \(a'\).
Řešení nápovědy 2
Pro zvětšení zrcadla platí vztahy:

\(Z=\frac{y'}{y}\) a \(Z=−\frac{a'}{a}\).

Porovnáním těchto dvou vztahů dostáváme: \[−\frac{a'}{a}=\frac{y'}{y}.\] Obě dvě strany rovnice vynásobíme \(−a\): \[a'=−a\frac{y'}{y}.\tag{3}\]
Nápověda 3
Do vztahu (2) dosaďte vztah (3) a výsledný vzorec dosaďte do rovnice (1).
Určete obecně poloměr křivosti \(r\).
Řešení nápovědy 3
Do vztahu (2) dosadíme za \(a'\) vztah (3): \[f=\frac{a\cdot \left(−a\frac{y'}{y}\right)}{a−a\frac{y'}{y}}. \] \(a\) vytkneme a vykrátíme: \[f=\frac{ −a\frac{y'}{y}}{1−\frac{y'}{y}}. \] Upravíme jmenovatel zlomku: \[f=\frac{ −a\frac{y'}{y}}{\frac{y−y'}{y}}. \] \(\frac{1}{y}\) vykrátíme: \[f=\frac{ −a\cdot y'}{y−y'}. \] Získaný vztah dosadíme za \(f\) do vztahu (1): \[r=2f=2\frac{ −a\cdot y'}{y−y'}.\]
Nápověda 4
Zamyslete se, jaké vlastnosti obrazu můžeme ze zadání určit. Z jakého důvodu v zápise zapisujeme velikost obrazu do absolutní hodnoty?

Určete číselně poloměr křivosti \(r\).
Řešení nápovědy 4

Velikost obrazu jsme zapsali do absolutní hodnoty \(|y'|=1 \mathrm{m}\), protože víme, jak je obraz vysoký, ale o jeho dalších vlastnostech nic nevíme.

To znamená, že \(y'=1 \mathrm{m}\) pro přímý obraz a \(y'=−1 \mathrm{m} \) pro převrácený obraz.

Číselné řešení

Ze zadání víme:

\(y= 2 \mathrm{m}\)

\(|y'|=1 \mathrm{m}\)

\(a=1{,}5 \mathrm{m}\)

Dosadíme hodnoty pro přímý obraz:

\(r=2\frac{ −a\cdot y'}{y−y'},\)

\(r=2\frac{ −1{,}5 {\cdot} 1}{2−1} \mathrm{m}= −3 \mathrm{m}.\)

Dosadíme hodnoty pro převrácený obraz:

\(r=2\frac{ −1{,}5 \cdot \left(−1\right)}{2+1} \mathrm{m}= 1 \mathrm{m}.\)
\[r=2\frac{ −a\cdot y'}{y−y'}.\]
Nápověda 5
Jaké známe typy kulových zrcadel? Jak souvisí typ kulového zrcadla s jeho poloměrem křivosti \(r\)? Určete o jaký typ kulového zrcadla se jedná v našem případě.
Řešení nápovědy 5

Kulové zrcadlo může být duté nebo vypuklé.

Pokud je poloměr křivosti menší než nula \(\left(r\lt 0 \right)\), pak se jedná o vypuklé zrcadlo.

Pokud je poloměr křivosti větší než nula \(\left(r\gt 0 \right)\), pak se jedná o duté zrcadlo.

V našem případě se jedná o vypuklé zrcadlo s poloměrem křivosti \(r=3 \mathrm{m}\) nebo o duté zrcadlo s poloměrem křivosti \(r=1 \mathrm{m}\).
Celkové řešení
Poloměr a ohnisková vzdálenost kulového zrcadla

Pro poloměr kulového zrcadla (dutého i vypuklého) platí vztah: \[r=2f,\tag{1}\] kde \(f\) je ohnisková vzdálenost zrcadla. Napíšeme zobrazovací rovnici pro kulové zrcadlo: \[\frac{1}{a}+\frac{1}{a'}=\frac{1}{f},\] kde \(a\) je vzdálenost mláděte žirafy od vrcholu kulového zrcadla a \(a'\) je vzdálenost obrazu mláděte žirafy od vrcholu kulového zrcadla.

Zlomky na levé straně rovnice převedeme na společného jmenovatele: \[\frac{a+a'}{a\cdot a'}=\frac{1}{f}.\]

Vyjádříme \(f\): \[f=\frac{a\cdot a'}{a+a'} \tag{2}\]

Vzdálenost obrazu mláděte žirafy od vrcholu zrcadla \(a'\)

Využijeme vztahy pro zvětšení zrcadla:

\(Z=\frac{y'}{y}\) a \(Z=−\frac{a'}{a}\).

Porovnáním těchto dvou vztahů dostáváme: \[−\frac{a'}{a}=\frac{y'}{y}.\] Obě dvě strany rovnice vynásobíme \(−a\): \[a'=−a\frac{y'}{y}.\tag{3}\]

Poloměr křivosti obecně

Do vztahu (2) dosadíme za \(a'\) vztah (3): \[f=\frac{a\cdot \left(−a\frac{y'}{y}\right)}{a−a\frac{y'}{y}}. \] \(a\) vytkneme a vykrátíme: \[f=\frac{ −a\frac{y'}{y}}{1−\frac{y'}{y}}. \] Upravíme jmenovatel zlomku: \[f=\frac{ −a\frac{y'}{y}}{\frac{y−y'}{y}}. \] \(\frac{1}{y}\) vykrátíme: \[f=\frac{ −a\cdot y'}{y−y'}. \] Získaný vztah dosadíme za \(f\) do vztahu (1): \[r=2f=2\frac{ −a\cdot y'}{y−y'}.\]

Poloměr křivosti číselně a typ kulového zrcadla

Velikost obrazu jsme v zápise zapsali do absolutní hodnoty \(|y'|=1 \mathrm{m}\), protože víme, jak je obraz vysoký, ale o jeho dalších vlastnostech nic nevíme.

Pro přímý obraz bude platit \(y'=1 \mathrm{m}\) a pro převrácený obraz \(y'=−1 \mathrm{m} \).

Číselné řešení

Ze zadání víme:

\(y= 2 \mathrm{m}\)

\(|y'|=1 \mathrm{m}\)

\(a=1{,}5 \mathrm{m}\)

Do vztahu pro výpočet poloměru kulového zrcadla dosadíme hodnoty pro přímý obraz:

\(r=2\frac{ −1{,}5 {\cdot} 1}{2−1} \mathrm{m}= −3 \mathrm{m}.\)

Protože poloměr křivosti je menší než nula \(\left(r\lt 0 \right)\), jedná se o vypuklé zrcadlo.

Nyní dosadíme hodnoty pro převrácený obraz:

\(r=2\frac{ −1{,}5 \cdot \left(−1\right)}{2+1} \mathrm{m}= 1 \mathrm{m}.\)

Protože poloměr křivosti je větší než nula \(\left(r\gt 0 \right)\), jedná se o duté zrcadlo.
Odpověď
Žirafa se dívá do vypuklého zrcadla s poloměrem křivosti \(3 \mathrm{m}\) nebo do dutého zrcadla s poloměrem křivosti \(1 \mathrm{m}\).