Interference vln šířících se různými směry
Úloha číslo: 1401
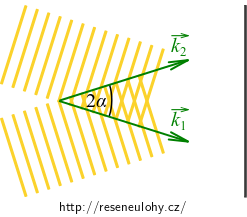
Ve vakuu se šíří dvě vlny o stejné frekvenci, jejichž vlnové vektory \(\vec{k}_1,\vec{k}_2\) svírají úhel \(2\alpha\). Tyto vlny dopadají na stínítko kolmé ke směru \(\vec{k}_1 + \vec{k}_2\). Předpokládejte, že amplituda elektrické intenzity obou vln je kolmá k rovině dané vektory \(\vec{k}_1\) a \(\vec{k}_2\). Použijte popis vln v komplexním formalismu
\[ \begin{eqnarray} \vec{E}_1 &=& \vec{E}_0 e^{i(\omega t - \vec{k}_1 \cdot \vec r)},\\ \quad \vec{E}_2 &=& \vec{E}_0 e^{i(\omega t - \vec{k}_2 \cdot \vec r)}. \end{eqnarray} \]Vypočtěte a popište průběh časové střední hodnoty objemové hustoty elektrické energie elektromagnetické vlny na stínítku.
Teorie
Pro řešení příkladu je potřeba znát popis rovinné vlny
\[ \vec{E} = \vec{E}_0 e^{i(\omega t - \vec{k} \cdot \vec r)}, \]kde \(\vec{k}\) je vlnový vektor mající směr šíření vlny a platí \(k = \frac{2\pi}{\lambda}\). Více o popisu rovinné vlny zde.
Využijeme také Eulerův vztah pro exponenciálu s komplexním exponentem
\[e^{i\varphi} = \cos \varphi + i \sin \varphi.\]Střední hodnota objemové hustoty elektrické energie elektromagnetické vlny ve vakuu s využitím komplexního formalismu lze vypočítat ze vztahu
\[w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^\star.\]Nápověda 1 – průběh intenzity na stínítku
Cílem je určit střední hodnotu objemové hustoty elektrické energie elektromagnetické vlny ve vakuu
\[w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^\star.\]Potřebujeme tedy vyjádření elektrické intenzity \(\vec{E}\) výsledné vlny. Nalezněte jej jako superpozici (součet) interferovaných vln.
Nápověda 2 – interferenční obrazec
Intenzita světla na stínítku je úměrná střední hodnotě prostorové hustoty elektrické energie vlny v daném místě. Rozborem nalezené funkce \(w_\mathrm{E}(x)\) popište vzniklý interferenční obrazec.
CELKOVÉ ŘEŠENÍ
Máme dány vlny s elektrickými intenzitami
\[\vec{E}_1 = \vec{E}_0 e^{i(\omega t - \vec{k}_1 \cdot \vec r)}, \quad \vec{E}_2 = \vec{E}_0 e^{i(\omega t - \vec{k}_2 \cdot \vec r)}.\]Jejich superpozicí získáme el. intenzitu výsledné vlny
\[ \vec{E} = \vec{E}_1 + \vec{E}_2 = \vec{E}_0 e^{i\omega t}\big( e^{-i\vec{k}_1 \cdot \vec{r}} + e^{-i\vec{k}_2 \cdot \vec{r}} \big). \]Tuto intenzitu je třeba dosadit do vztahu pro střední hustotu el. energie
\[ w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^\star. \]Proveďme proto nejprve skalární součin výrazů
\[\vec{E} = \vec{E}_0 e^{i\omega t}\big( e^{-i\vec{k}_1 \cdot \vec{r}} + e^{-i\vec{k}_2 \cdot \vec{r}} \big) \quad \mathrm{a} \quad \vec{E}^\star = \vec{E}_0 e^{-i\omega t}\big( e^{i\vec{k}_1 \cdot \vec{r}} + e^{i\vec{k}_2 \cdot \vec{r}} \big). \]Tedy
\[ \vec{E}\cdot \vec{E}^\star = E_0^2 e^{i\omega t - i\omega t} \big( e^{-i\vec{k}_1 \cdot \vec{r}} + e^{-i\vec{k}_2 \cdot \vec{r}} \big)\big( e^{i\vec{k}_1 \cdot \vec{r}} + e^{i\vec{k}_2 \cdot \vec{r}} \big)= \] \[ =E_0^2 \left( e^{-i(\vec{k}_1 -\vec{k}_1) \cdot \vec{r}} + e^{ i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + e^{-i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + e^{-i(\vec{k}_2 -\vec{k}_2) \cdot \vec{r}} \right)= \] \[ = E_0^2 \left( 1 + e^{ i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + e^{-i(\vec{k}_2 -\vec{k}_1) \cdot \vec{r}} + 1 \right)= \]Komplexní exponenciálu rozepíšeme z Eulerova vztahu \(e^{i\varphi} = \cos \varphi + i \sin \varphi \)
\[ \small{= E_0^2 \left[ 2 + \cos \vec{r}\cdot(\vec{k}_2 -\vec{k}_1) + i\sin\vec{r}\cdot (\vec{k}_2 -\vec{k}_1) + \cos \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) - i\sin \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) \right] = } \] \[ =E_0^2 \left[ 2 + 2\cos \left(\vec{r}\cdot \left(\vec{k}_2 -\vec{k}_1\right)\right) \right] = 2E_0^2 \left[ 1 + \cos \left(\vec{r}\cdot \left(\vec{k}_2 -\vec{k}_1\right)\right) \right].\]Dosazením vypočítaného do vztahu pro hustotu el. energie pak máme
\[ w_\mathrm{E} = \frac{1}{4}\varepsilon_0\, \vec{E}\cdot\vec{E}^\star = \frac{E_0^2}{2}\varepsilon_0 \left[1 + \cos \left(\vec{r}\cdot (\vec{k}_2 -\vec{k}_1)\right) \right]. \]Upravme zvlášť skalární součin \(\vec{r}\cdot (\vec{k}_2 -\vec{k}_1)\) v argumentu kosinu.
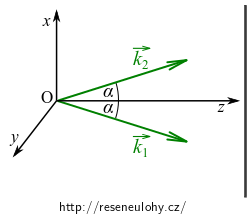
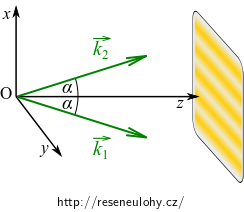
Zavedeme-li kartézský systém souřadnic podle obrázku, skalární součin se po rozepsání zjednoduší
\[ \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) = x(k_{2x} - k_{1x})+ y(\underbrace{k_{2y} - k_{1y}}_{0})+ z(\underbrace{k_{2z} - k_{1z}}_{0}) = x(k_{2x} - k_{1x}). \]neboť \(y\)-ové i \(z\)-ové složky vlnových vektorů jsou stejné.
Vlny mají stejnou frekvenci, proto je stejná i velikost vlnových vektorů – označme ji \(k\).
Podle následujícího obrázku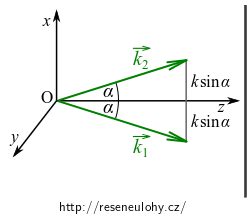
lze rozdíl \(x\)-ových složek vlnových vektorů vyjádřit jako \(2k\sin\alpha\), čímž dostáváme následující výraz pro skalární součin
\[ \vec{r}\cdot (\vec{k}_2 -\vec{k}_1) = 2kx\sin\alpha. \]Užitím právě odvozeného vyjádření skalárního součinu dostáváme konečný vztah pro prostorovou hustotu elektrické energie
\[ w_\mathrm{E}= \frac{E_0^2}{2}\varepsilon_0 \left[ 1 + \cos (2kx\sin\alpha) \right]. \]Ta je závislá pouze na souřadnici \(x\) (svislá osa), se souřadnicí \(y\) (osa směřující před nákresnu) se nemění.
Použijeme-li navíc goniometrický vztah \(\frac{1+\cos \varphi}{2} = \cos^2 \frac{\varphi}{2}\), dostaneme následující průběh střední hodnoty prostorové hustoty elektrické energie
\[ w_\mathrm{E}(x) = E_0^2\,\varepsilon_0 \cos^2 (kx\sin\alpha), \]Povahu interferenčního obrazce ve smyslu relativního osvětlení stínítka tedy určuje funkce
\[ I_r(x) = \cos^2 (kx\sin\alpha). \]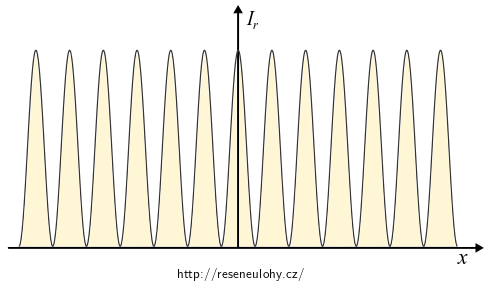
Na stínítku se objeví proužky mající směr osy \(y\).
Vypočítejme, na čem závisí šířka interferenčních proužků. Za šířku proužku budeme považovat vzdálenost sousedních minim. Intenzita světla na stínítku je minimální, jestliže
\[ \cos^2 (kx\sin\alpha) = 0, \quad\text{ tj. když }\quad kx\sin\alpha = \frac{\pi}{2} + m\pi,\quad m\in\mathbb{Z}. \]Chceme-li určit vzdálenost libovolných dvou sousedních minim, napíšeme tuto podmínku pro \(m\)-té a \((m+1)\)-ní minimum, které nastává na souřadnicích \(x_1\) a \(x_2\)
\[ \begin{eqnarray} kx_1\sin\alpha &=& \frac{\pi}{2} + m\pi \\ kx_2\sin\alpha &=& \frac{\pi}{2} + (m+1)\pi, \end{eqnarray} \]rovnice odečteme
\[ k(\underbrace{x_2 - x_1}_{\Delta x}) \sin\alpha = \pi \]a vyjádříme hledanou šířku
\[ \Delta x = \frac{\pi}{k\sin\alpha}. \]Dosazením \(\frac{2\pi}{\lambda}\) za velikost vlnového vektoru \(k\) dostaneme konečný vztah
\[ \Delta x = \frac{\lambda}{2\sin\alpha}. \]Z tohoto vztahu plyne, že pro větší vlnové délky bude interferenční obrazec širší, naopak s rostoucí odchylkou paprsků se bude zhušťovat.
Odpověď
Průběh střední hodnoty prostorové hustoty elektrické energie na stínítku je
\[ w_\mathrm{E}(x) = E_0^2\,\varepsilon_0\, \cos^2 (kx\sin\alpha), \] Relativní osvětlení stínítka určuje funkce \[ I_r(x) = \cos^2 (kx\sin\alpha). \]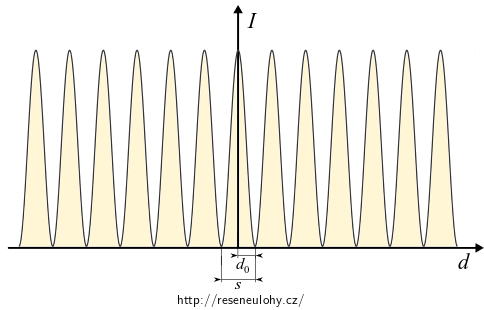
Šířka proužků interferenčního obrazce (vzdálenost sousedních minim) je
\[ \Delta x = \frac{\lambda}{2\sin\alpha}. \]Pro větší vlnové délky bude interferenční obrazec širší, naopak s rostoucí odchylkou paprsků se bude zhušťovat.
Poznámka: „Stavíme“ rovinnou harmonickou vlnu (komplexní formalismus)
V této části postupným zobecňováním rovnice vlny v přímce dospějeme k rovnici komplexní rovinné vlny.
Již ze střední školy z nauky o mechanickém vlnění si možná pamatujeme, že postupnou harmonickou vlnu na přímce můžeme popsat rovnicí
\[ y(x,t) = y_0 \cos \left[\omega \left( t - \frac{x}{v}\right)\right]. \]Nejde o nic jiného, než o zobecnění rovnice harmonického oscilátoru, uvědoměním si, že v místě vzdáleném \(x\) od zdroje je v čase \(t\) okamžitá výchylka stejná, jako byla v čase \(t-\frac{x}{v}\) na zdroji, kde podíl \(\frac{x}{v}\) je čas, po který se vlna do daného místa šíří.
V našem optickém příkladě nejde však o žádnou fyzickou výchylku \(y\), ale o vektor elektrické intenzity \(\vec{E}\). Rychlost šíření světla se obvykle značí \(c\), takže po přepsání máme
\[ \vec{E} = \vec{E}_0 \cos \left[\omega \left( t - \frac{x}{c}\right)\right]. \]Vektor elektrické intenzity je nyní přiřazen každému bodu přímky šíření. Stavíme ale vlnu rovinnou, proto bychom chtěli, aby tyto hodnoty byly přiřazeny i všem bodům v kolmých rovinách na směr šíření.
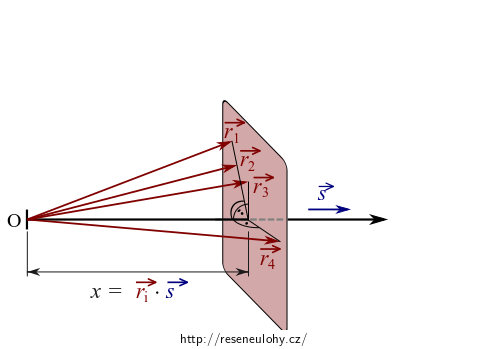
Každá taková rovina je tvořena body, jejichž polohové vektory \(\vec{r}\) mají stejný průmět \(x\) do směru šíření \(\vec{s}\). Proto lze psát
\[\vec{r} \cdot \vec{s} = x.\]Dostáváme tak rovnici rovinné vlny ve tvaru
\[ \vec{E} = \vec{E}_0 \cos \left[\omega \left( t - \frac{\vec{r} \cdot \vec{s}}{c}\right)\right] = \vec{E}_0 \cos \left(\omega t - \omega \frac{\vec{r} \cdot \vec{s}}{c}\right). \]Druhý člen v argumentu je dost složitý. Zjednodušme jej
\[ \omega \frac{\vec{r} \cdot \vec{s}}{c} = 2\pi \nu \frac{\vec{r} \cdot \vec{s}}{c} = 2\pi \frac{c}{\lambda} \frac{\vec{r} \cdot \vec{s}}{c} = \underbrace{\frac{2\pi}{\lambda}\vec{s}}_{\mathrm{ozn.}\,\vec{k}} \cdot\vec{r} = \vec{k}\cdot\vec{r}. \]Při úpravě jsme použili vztahy \(\omega = 2\pi \nu\) a \(\lambda = \frac{c}{\nu}\). Zavedli jsme vlnový vektor \(\vec{k}\), který má směr šíření vlny a jehož velikost je zde pro rovinnou monochormatickou vlnu rovna \(\frac{2\pi}{\lambda}\).
Rovinná vlna má nyní sice poměrně elegantní tvar
\[ \vec{E} = \vec{E}_0 \cos \left(\omega t - \vec{k} \cdot \vec{r} \right), \]ale práce s tímto tvarem, například při superpozici vln, není šikovná – vede na sčítání goniometrických funkcí s různými argumenty. Proto zavedeme komplexní vyjádření vlny. Pracujme ve vší obecnosti, dodejme do argumentu počáteční fázi \(\varphi_0\)
\[ \vec{E} = \vec{E}_0 \cos \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right). \]K tomuto reálnému vyjádření přičteme komplexní vektorovou funkci
\[i \vec{E}_0 \sin \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right),\]čímž vznikne komplexní vlna
\[ \overset{\sim}{\vec E} = \vec{E}_0 \cos \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right) + i \vec{E}_0 \sin \left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right). \]Z definice komplexní exponenciály \(e^{i\alpha} = \cos\alpha + i\sin \alpha\) pak máme
\[ \overset{\sim}{\vec E} = \vec{E}_0 e^{i\left(\omega t - \vec{k} \cdot \vec{r} + \varphi_0 \right)} = \underbrace{\vec{E}_0 e^{i\varphi_0 }}_{\mathrm{ozn.\,}\overset{\sim}{\vec{E}_0}} e^{i\left(\omega t - \vec{k} \cdot \vec{r}\right)} = \overset{\sim}{\vec{E}_0} e^{i\left(\omega t - \vec{k} \cdot \vec{r}\right)}. \]kde jsme zavedli komplexní amplitudu \(\overset{\sim}{\vec{E}_0}\), která v sobě kromě informace o velikosti vlny zahrnuje i její počáteční fázi.
Tam, kde je optika lineární, lze libovolné komplexní vlny sčítat, s exponenciálními funkcemi se pracuje dobře. V okamžiku, kdy nás zajímá reálný průběh, podíváme se na reálnou část komplexní vny, tj.
\[ \vec{E} = \mathrm{Re\,} \overset{\sim}{\vec{E}}. \]Obvykle se nad komplexní veličiny symboly \(\sim\) nepíší. Že se jedná o komplexní veličinu je poznat z přítomnosti komplexní exponenciály. V této úloze budeme vlnky také vynechávat.
Poznamenejme, že v tomto případě je použití komplexního formalismu pouze matematický „zlepšovák“, imaginární část nemá žádný fyzikální význam.



