Sbírka řešených úloh

Výpočet šířky spektra

Úloha číslo: 1649

• Obrázek

  

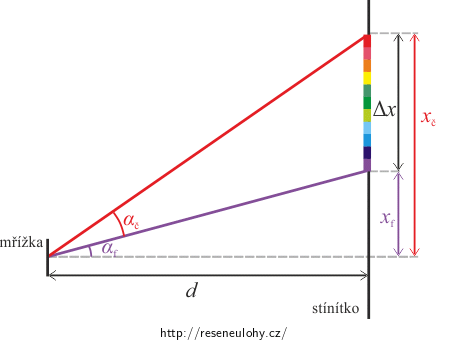
  Na obrázku jsme vyznačili: d je vzdálenost mřížky od stínítka, x_f je vzdálenost fialového maxima prvního řádu od nultého řádu a úhel α_f je jeho odchýlení, x_č je vzdálenost červeného maxima prvního řádu od nultého řádu a úhel α_č je jeho odchýlení, Δx je šířka spektra, které se objeví na stínítku.

• Nápověda 1

  Pokuste se najít vztah pro úhly α_f a α_č pomocí dráhového rozdílu Δl a mřížkové konstanty b.

• Řešení nápovědy 1

  Pro úhel α_č platí:

  \[\sin\,α_\mathrm{č} = \, \frac{\mathrm{Δ}l_\mathrm{č}}{b},\]

  kde Δl_č je dráhový rozdíl a b je mřížková konstanta.

  Pro úhel α_f platí obdobně:

  \[\sin\,α_\mathrm{f} = \, \frac{\mathrm{Δ}l_\mathrm{f}}{b}.\]

  Podrobné odvození najdete v úloze Výpočet úhlu odchýlení maxima.

  Jelikož v úloze počítáme maxima, dosadíme za Δl = kλ a za k dosadíme řád maxima, tedy k = 1.

  Za vlnovou délku λ dosadíme vlnovou délku příslušného světla:

  \[\sin\,α_č = \, \frac{λ_\mathrm{č}}{b}\quad \mathrm{a} \quad \sin\,α_f = \, \frac{λ_\mathrm{f}}{b}.\]

  Teď vyjádříme úhly α_č a α_f.

• Nápověda 2

  Vyjádřete si pomocí obrázku (viz výše) šířku spektra Δx pomocí jednotlivých vzdáleností x_f, x_č a úhlů α_f, α_č.

• Řešení nápovědy 2

  Abychom mohli spočítat šířku spektra Δx, potřebujeme si tuto šířku vyjádřit pomocí veličin, které známe. Šířku spektra na stínítku Δx si jednoduše napíšeme jako rozdíl vzdáleností x_f a x_č.

  \[\mathrm{Δ}x=\, x_\mathrm{č} − x_\mathrm{f}, \]

  kde x_č si můžeme z obrázku (viz výše) vyjádřit jako:

  \[x_\mathrm{č}=\, d\,\mathrm{tg}\,\,α_\mathrm{č},\]

  stějně najdeme vztah pro x_f:

  \[x_\mathrm{f}=\, d\,\mathrm{tg}\,\,α_\mathrm{f}.\]

  Dosadíme si tyto vztahy do vztahu pro Δx a dostaneme:

  \[\mathrm{Δ}x=\, d\,\mathrm{tg}\,\,α_\mathrm{č} − d\,\mathrm{tg}\,\,α_\mathrm{f}= \, d\left(\mathrm{tg}\,\,α_\mathrm{č} − \mathrm{tg}\,\,α_\mathrm{f}\right).\]

  Úhly odchýlení α_č a α_f jsme odvodili v předchozí nápovědě, takže je můžeme dosadit a vypočítat šířku spektra.

• Zápis

  b = 0,01 mm =10−5 m	mřížková konstanta
  d = 3 m	vzdálenost mřížky od stínítka
  k = 1	řád maxima
  λf = 390 nm = 3,9·10−7 m	vlnová délka fialového světla
  λč = 790 nm = 7,9·10−7 m	vlnová délka červeného světla
  Δx = ? (cm)	šířka spektra

• Řešení

  

  Na obrázku jsme vyznačili: d je vzdálenost mřížky od stínítka, x_f je vzdálenost fialového maxima prvního řádu od nultého řádu a úhel α_f je jeho odchýlení, x_č je vzdálenost červeného maxima prvního řádu od nultého řádu a úhel α_č je jeho odchýlení, Δx je šířka spektra, které se objeví na stínítku.

  Chceme-li vypočítat šířku spektra na stínítku Δx, vyjádříme si tuto vzdálenost pomocí jednotlivých vzdáleností x_f, x_č a úhlů α_f, α_č.

  \[\mathrm{Δ}x=\, x_\mathrm{č} − x_\mathrm{f}=\, d\,\mathrm{tg}\,\,α_\mathrm{č} − d\,\mathrm{tg}\,\,α_\mathrm{f}=\,d\left(\mathrm{tg}\,\,α_\mathrm{č} − \mathrm{tg}\,\,α_\mathrm{f}\right).\]

  V tomto vztahu neznáme úhly odchýlení α_č a α_f. Pro tyto úhly platí vztahy:

  \[\sin\,α_\mathrm{č} = \, \frac{\mathrm{Δ}l_\mathrm{č}}{b} \quad \mathrm{a} \quad \sin\,α_\mathrm{f} = \, \frac{\mathrm{Δ}l_\mathrm{f}}{b},\]

  kde si za Δl dosadíme vztah pro interferenční maxima Δl = kλ a dosadíme k = 1. Za vlnovou délku λ dosadíme vlnovou délku světla příslušné barvy:

  \[\sin\,α_č = \, \frac{λ_\mathrm{č}}{b} \quad \mathrm{a} \quad \sin\,α_f = \, \frac{λ_\mathrm{f}}{b}.\]

  Teď si vyjádříme samotné úhly α_č a α_f a dosadíme do vztahu pro Δx.

  \[α_č = \,\arcsin\, \frac{λ_\mathrm{č}}{b} \quad \mathrm{a} \quad α_f = \,\arcsin\, \frac{λ_\mathrm{f}}{b}.\]

  Dosadíme hodnoty:

  \[\mathrm{Δ}x=\,\,d\left(\mathrm{tg}\,\,α_\mathrm{č} − \mathrm{tg}\,\,α_\mathrm{f}\right)=\, d\left(\mathrm{tg}\,\,\arcsin\, \frac{λ_\mathrm{č}}{b} − \mathrm{tg}\,\,\arcsin\, \frac{λ_\mathrm{f}}{b}\right)=\] \[=\, 3(\mathrm{tg}\,\,\arcsin\, \frac{7{,}9{\cdot}10^{−7}}{10^{−5}} − \mathrm{tg}\,\,\arcsin\, \frac{3{,}9{\cdot}10^{−7}}{10^{−5}})\,\dot{=}\,0{,}12\,\mathrm{m} = 12\,\mathrm{cm}.\]

• Odpověď

  Šířka spojitého spektra prvního řádu, které vznikne na stínítku vzdáleném 3 m, je 12 cm.

• Komentář

  Když se zamyslíme nad velikostí úhlu odchýlení červeného a fialového světla, zjistíme, že se jedná o velmi malé úhly. Pro takové úhly platí

  \[\sin\,\alpha\ \dot{=}\ \, \alpha\ \dot{=}\ \mathrm{tg}\,\,\alpha,\]

  kde prostřední rovnost platí, pokud je uvažovaný úhel dosazen v radiánech. Výpočet provedeme znovu, ale s výše uvedeným zanedbáním.

  Vypočítáme si úhly a hodnoty sin α a tg α, abychom viděli, že toto přiblížení v našem případě platí dostatečně přesně.

  \[\sin\,\alpha_\mathrm{č} =\, \frac{\lambda_\mathrm{č}}{b}= \,\frac{7{,}9{\cdot}10^{−7}}{10^\mathrm{−5}}=\,0{,}0790, \] \[\alpha_\mathrm{č}\dot=\,0{,}0791 \qquad \Rightarrow\qquad \mathrm{tg}\,\,\alpha_\mathrm{č}\ \dot{=}\ 0{,}0792,\] \[\sin\,\alpha_\mathrm{f} =\, \frac{\lambda_\mathrm{f}}{b}= \,\frac{3{,}9{\cdot}10^{−7}}{10^\mathrm{−5}}=\,0{,}0390,\] \[\alpha_\mathrm{č}\dot=\,0{,}03901 \qquad \Rightarrow\qquad\mathrm{tg}\,\,\alpha_\mathrm{f}\ \dot{=}\ \,0{,}03902,\]

   

  Z obrázku dostaneme vztahy pro úhly odchýlení α_č a α_f:

  \[\frac{x_\mathrm{č}}{d}=\,\mathrm{tg}\,\,\alpha_\mathrm{č}\ \dot{=}\ \,\alpha_\mathrm{č}\ \dot{=}\ \,\sin\,\alpha_\mathrm{č} = \frac{\mathrm{\Delta}l_\mathrm{č}}{b},\] \[\frac{x_\mathrm{f}}{d}=\,\mathrm{tg}\,\,\alpha_\mathrm{f}\ \dot{=}\ \,\alpha_\mathrm{f}\ \dot{=}\ \,\sin\,\alpha_\mathrm{f} = \frac{\mathrm{\Delta}l_\mathrm{f}}{b},\]

  kde si za Δl dosadíme vztah pro interferenční maxima Δl = kλ, dosadíme k = 1 a vyjádříme si x_č a x_f.

  \[\mathrm{\Delta}x=\, x_\mathrm{č} − x_\mathrm{f}=\,\frac{d}{b}\left(\lambda_\mathrm{č} − \lambda_\mathrm{f}\right)\]

  a dosadíme hodnoty ze zadání

  \[\mathrm{\Delta}x=\,\frac{3}{10^\mathrm{−5}}\cdot\left(7{,}9{\cdot}10^{−7} − 3{,}9{\cdot}10^{−7}\right)\,\mathrm{m}= \,0{,}12\,\mathrm{m}=\,12\,\mathrm{cm}.\]

  Jak můžeme vidět, i když jsme použili zanedbání, na výsledku se nic nezměnilo.

• Odkaz na pokus

  Experiment ukazující rozklad bílého světla na barvy s využitím optické mřížky: Difrakce bílého světla na optické mřížce