Ohyb na štěrbině
Úloha číslo: 1504
Na nekonečně dlouhou štěrbinu šířky \(d\) dopadá harmonická rovinná vlna. Předpokládejte kolmý dopad a určete průběh intenzity světla na stínítku, které je ve vzdálenosti \(l\) od roviny clony a je s ní rovnoběžné. Nakreslete průběh intenzity na stínítku a vypočítejte šířku proužků ohybového obrazce.
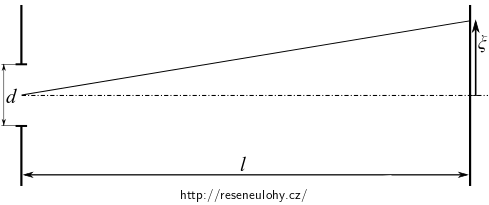
Uvažujte tzv. Fraunhoferův ohyb, tj. případ, kdy je stínítko velmi daleko.
Rozbor
Nekonečnou štěrbinu dané šířky lze modelovat jako spojitý pás přímkových zdrojů válcových vln.
Pás přímkových zdrojů je na obrázku znázorněn úsečkou kolmých žlutých bodových průmětů.
Elektrickou intenzitu harmonické válcové vlny lze popsat funkcí
\[ E_\mathrm{válc}(\rho) = \frac{\mathcal{E}_0}{\sqrt{\rho}}e^{i(\omega t - k\rho)}, \]kde \(\mathcal{E}_0\) je konstanta související s elektrickou intenzitou na clonu dopadající vlny, \(\rho\) je válcová souřadnice a \(k=\frac{2\pi}{\lambda}\).
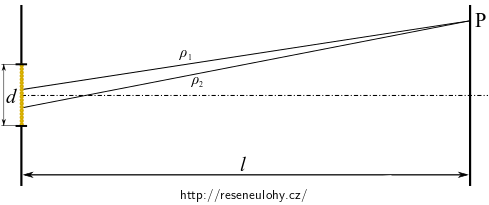
Do bodu P na stínítku přicházejí válcové vlny z různých částí štěrbiny s různými souřadnicemi \(\rho\) a interferují. Výslednou elektrickou intenzitu nalezneme jako superpozici příspěvků přímkových zdrojů přes celou štěrbinu.
Je-li stínítko dostatečně daleko, bude možné části válcových vlnoploch, jak ukážeme později, považovat za téměř rovinné a pro výpočet intenzity světla užít vztah platný pro rovinnou vlnu
\[ I = \frac{1}{2z_0} EE^\star, \]kde \(E\) je el. intenzita superponovaných vln a \(z_0 = \sqrt{\frac{\mu_0}{\varepsilon_0}}\) je konstanta a značí charakteristickou impedanci vakua.
Z povahy válcových vln vyplývá, že intenzita na stínítku bude translačně symetrická ve směru rovnoběžném se štěrbinou.
Nápověda 1 – elektrická intenzita
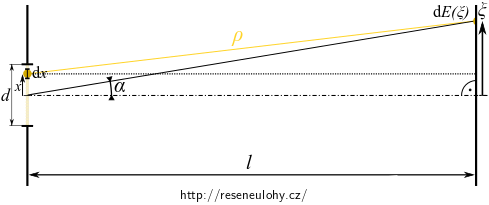
Napište vyjádření válcové vlny elementárního zdroje šířky \(\mathrm{d}x\) na souřadnici \(x\).
Dále vyjádřete souřadnici \(\rho\) pomocí vzdálenosti \(l\), souřadnice \(x\) myšleného elementárního zdroje a souřadnice místa na stínítku \(\xi\). Výraz upravte s uvážením \(x \lt d\ll l\).
Výsledná elektrická intenzita je dána součtem příspěvků od všech elementárních zdrojů štěrbiny, které si představujme jako tenké „pásky“ zdrojů válcových vln. Tyto pásky ji pokrývají spojitě, sestavte tedy příslušný integrál.
Nápověda 2 – výpočet integrálu
Určete integrál, ke kterému jsme dospěli v předchozím oddílu
\[ E(\xi) = \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]Tímto integrálem „nasčítáváme“ příspěvky elektrických intenzit v místě \(\xi\) stínítka od jednotlivých elementárních zdrojů štěrbiny.
Exponenciálu rozepište v součin exponenciálních funkcí, členy nezávisející na integrační proměnné \(x\) „vytkněte“ před integrál. Integrál vypočtete snadno, neboť \(\int e^{\varphi x}\,\mathrm{d}x = \frac{e^{\varphi x}}{\varphi}+C\).
K nalezené funkci \(E(\xi)\) určete komplexní sdružení \(E^\star(\xi)\).
Nápověda 3 – průběh intenzity na stínítku
Ve velké vzdálenosti od štěrbiny lze části válcových vln považovat za rovinné a intenzitu světla tak lze vypočítat pomocí vztahu
\[ I = \frac{1}{2z_0} EE^\star. \]Nápověda 4 – rozbor ohybového obrazce
Určete šířku hlavních a vedlejších proužků difrakčního obrazce.
CELKOVÉ ŘEŠENÍ

Příspěvek k elektrické intenzitě na stínítku v místě o souřadnici \(\xi\), příslušící elementárnímu zdroji šířky \(\mathrm{d}x\) na souřadnici \(x\) štěrbiny, je
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{\rho}} e^{i(\omega t - k\rho)} \mathrm{d}x, \tag{1}\]kde \(E_0\) je konstanta (\([E_0]=\mathrm{V}\cdot\mathrm{m^{-\frac{3}{2}}}\)) a \(\rho\) je vzdálenost linie na stínítku od přímkového zdroje a lze vyjádřit pomocí \(l,\xi, x\) jako
\[ \rho = \sqrt{l^2 + (\xi-x)^2}. \]Nyní provedeme dvě aproximace:
-
Zanedbání změny úbytku amplitudy v rámci stínítka.
Ve vztahu (1) klesá amplituda elektrické intenzity s \(\sqrt\rho\). Je-li stínítko dostatečně daleko, jsou rozdíly \(\rho\) a tedy i rozdíly globální amplitudy zanedbatelné a proměnný výraz \(\frac{1}{\sqrt\rho}\) můžeme aproximovat konstantou \(\frac{1}{\sqrt{l}}\) To nám umožní v budoucnu snadno integrovat. Úpravu \(\rho\) s přihlédnutím k \(|x| \lt d \ll l\).
Upravme výraz pro \(\rho\) \[ \rho = \sqrt{l^2 + (\xi-x)^2} = \sqrt{l^2 + \xi^2 - 2\xi x + x^2} = \] \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{grey}{\frac{x^2}{l^2 + \xi^2}}}= \] Šedý člen vypustíme, je pro velká \(l\) řádově zanedbatelný a místo něj vřadíme zanedbatelně malý člen (modře) k úpravě výrazu pod odmocninou na úplný čtverec. \[ = \sqrt{l^2 + \xi^2} \sqrt{1 - \frac{2\xi x}{l^2 + \xi^2} + \color{blue}{\frac{\xi^2 x^2}{\left(l^2 + \xi^2\right)^2}}}= \] \[ = \sqrt{l^2 + \xi^2}\bigg(1-\frac{\xi x}{l^2 + \xi^2} \bigg)= \] \[ = \sqrt{l^2 + \xi^2}-x\overbrace{\frac{\xi}{\sqrt{l^2 + \xi^2}}}^{\sin \alpha} =\sqrt{l^2 + \xi^2} - x\sin \alpha. \]
Předchozí aproximace nám dávají následující tvar příspěvku elektrické intenzity
\[ \mathrm{d}E_x(\xi)=\frac{E_0}{\sqrt{l}} e^{i(\omega t - k\rho)}\mathrm{d}x, \qquad \mathrm{kde\,} \rho = \sqrt{l^2 + \xi^2} - x\sin \alpha. \]Celková elektrická intenzita na souřadnici \(\xi\) stínítka je dána součtem příspěvků intenzit ode všech elementárních zdrojů ve štěrbině od \(x=-\frac{d}{2}\) do \(\frac{d}{2}\). Tedy
\[ E(\xi) = \int_\mathrm{štěrb.}\mathrm{d}E_x(\xi) = \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x. \]Tento integrál vypočítáme
\[ E(\xi) = \int_{-\frac{d}{2}}^{\frac{d}{2}} \frac{E_0}{\sqrt{l}} e^{i\left[\omega t - k\big( \sqrt{l^2 + \xi^2} - x\sin \alpha\big)\right]}\,\mathrm{d}x = \]členy nezávislé na \(x\) vytkneme před integrál
\[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \int_{-\frac{d}{2}}^{\frac{d}{2}} e^{ikx\sin \alpha}\,\mathrm{d}x = \] \[ = \frac{E_0}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left[ \frac{e^{ikx\sin \alpha}}{ik\sin\alpha} \right]_{-\frac{d}{2}}^{\,\,\frac{d}{2}}= \] \[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \left( e^{ik\frac{d}{2}\sin \alpha} - e^{-ik\frac{d}{2}\sin \alpha} \right)= \]Označme \(\psi = k\frac{d}{2}\sin \alpha\).
Nyní samostatně upravíme komplexní exponenciály v závorce. Převedeme je do goniometrického tvaru (\(e^{i\varphi} = \cos \varphi + i \sin \varphi\)).
\[ e^{i\psi} - e^{-i\psi} = \cos \psi + i\sin \psi - \cos( -\psi) - i\sin (-\psi) = 2i\sin\psi. \]Máme tedy
\[ = \frac{E_0}{\sqrt{l}ik\sin\alpha} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} 2i\sin\psi= \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}. \]kde jsme za \(\sin\alpha\) dosadili ze substitučního vztahu \(\psi = k\frac{d}{2}\sin \alpha\) výraz \(\frac{2\psi}{kd}\).
K právě určené elektrické intenzitě
\[ E(\xi) = \frac{E_0d}{\sqrt{l}} e^{i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}, \tag{3}\]napíšeme její komplexní sdružení
\[ E^\star(\xi)= \frac{E_0d}{\sqrt{l}} e^{-i(\omega t - k\sqrt{l^2 + \xi^2})} \frac{\sin\psi}{\psi}. \tag{4}\]Průběh intenzity světla získáme dosazením (3) a (4)
\[ I = \frac{1}{2z_0} EE^\star= \overbrace{\frac{E_0^2 d^2}{2z_0l}}^{\mathrm{ozn.\,}I_0} \underbrace{e^{i(\cdots)}e^{-i(\cdots)}}_{1} \frac{\sin^2 \psi}{\psi^2} = I_0 \frac{\sin^2 \psi}{\psi^2}, \] \[ \mathrm{kde}\qquad \psi = k\frac{d}{2}\sin \alpha. \]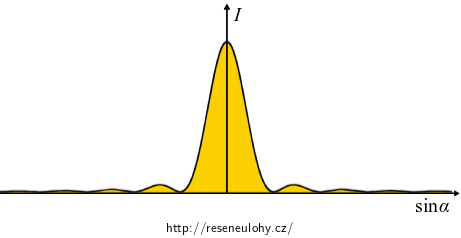
Uprostřed stínítka bude centrální velmi intenzivní maximum, které bude lemováno maximy vedlejšími, s rostoucí vzdáleností méně a méně intenzivními.
Proveďme rozbor ohybové funkce průběhu intenzity
\[ I = I_0 \frac{\sin^2 \psi}{\psi^2}, \qquad \mathrm{kde}\qquad I_0 = \frac{E_0^2 d^2}{2z_0l}\quad \mathrm{a}\quad \psi = k\frac{d}{2}\sin \alpha. \]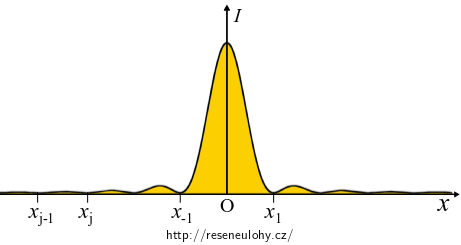
Pro \(\psi = 0\) nabývá ohybová funkce maxima \(I_0\), neboť
\[ I_0 \frac{\sin^2\psi}{\psi^2} \le I_0\frac{1}{\psi^2} \qquad \mathrm{a}\qquad \lim_{\psi \to 0} I_0 \frac{\sin^2\psi}{\psi^2} = I_0. \]Je-li úhel \(\alpha\) malý, pak je
\[ \sin \alpha \,\approx\, \tan \alpha = \frac{x}{l}. \]Minima intenzity světla nastanou za podmínky
\[ \begin{eqnarray} \psi &=& m\pi, \quad m\in \mathbb{Z}\setminus\lbrace 0 \rbrace \\ k\frac{d}{2}\sin \alpha_m &=& m\pi \\ k\frac{d}{2} \frac{x_m}{l} &=& m\pi \quad \Rightarrow \quad x_m = m\frac{2\pi l}{kd} = m\frac{\lambda l }{d}, \end{eqnarray} \]kde jsme použili vztah \(k=\frac{2\pi}{\lambda}\).
Šířka centrálního proužku je tedy
\[ s= x_1 - x_{-1} = \frac{\lambda l}{d}-\left(-\frac{\lambda l}{d}\right) = \frac{2\lambda l}{d}. \]Šířka ostatních proužků je poloviční, neboť
\[s^\prime = \underbrace{x_j - x_{j-1}}_{j\in\mathbb{Z}\setminus \lbrace 0,{}1 \rbrace} = j\frac{\lambda l}{d}-(j-1)\frac{\lambda l}{d}=\frac{\lambda l}{d}.\]Rozměry ohybového obrazce jsou při Fraunhoferově difrakci úměrné \(\frac{\lambda l}{d}. \)
Se zvětšující se vzdáleností \(l\) stínítka od mřížky a s rostoucí vlnovou délkou \(\lambda\) se bude difrakční obrazec rozšiřovat, se zvětšováním šířky štěrbiny \(d\) se bude naopak zhušťovat.
-
Odpověď
Průběh intenzity při ohybu na štěrbině
\[ I = I_0 \frac{\sin^2 \psi}{\psi^2}, \] \[ \mathrm{kde}\qquad I_0 = \frac{E_0^2 d^2}{2z_0l}\quad \mathrm{a}\quad \psi = k\frac{d}{2}\sin \alpha. \]
Šířka centrálního proužku je \(\frac{2\lambda l}{d}\), šířka proužků vedlejších je poloviční.
Se zvětšující se vzdáleností \(l\) stínítka od mřížky a s rostoucí vlnovou délkou \(\lambda\) se bude difrakční obrazec rozšiřovat, se zvětšováním šířky štěrbiny \(d\) se bude naopak zhušťovat.

Na obrázku ohybový obrazec vytvořený v domácích podmínkách. Laserové ukazovátko svítí skrz štěrbinu vytvořenou mírně rozevřenými ostří štípacích kleští na vzdálenou zeď.


