Sbírka řešených úloh

Poloha prvního maxima při interferenci dvou koherentních zdrojů

Úloha číslo: 1621

• Nápověda 1

  Jaký je dráhový rozdíl paprsků, které vycházejí z obou zdrojů a dopadají na stejné místo na stínítku?

• Řešení nápovědy 1

  Nakreslíme si obrázek, kde máme dva bodové zdroje záření, které vysílají světlo. Paprsky dopadají do jednoho bodu A na stínítku.

  

  Z₁ a Z₂ jsou zdroje světla a d je vzdálenost zdrojů od stínítka. Nakreslíme si zvětšeně oblast zdrojů světla a budeme přepokládat, že naše stínítko je tak daleko od mřížky, že paprsky přicházející do určitého bodu A stínítka jsou přesto přibližně rovnoběžné, když opouštějí zdroje.

  

  Na obrázku z trojúhelníku získáme vztah pro dráhový rozdíl:

  \[\mathrm{\Delta}l = \,b\sin\,\alpha,\]

  kde Δl je dráhový rozdíl dvou sousedních paprsků, b je vzdálenost zdrojů a α je úhel, který paprsky svírají s centrální osou.

  V bodě A mohou vzniknout interferenční maxima, nebo minima – to záleží na velikosti dráhového rozdílu sousedních paprsků.

• Nápověda 2

  Jakou hodnotu musí mít dráhový rozdíl, aby vzniklo interferenční maximum?

• Řešení nápovědy 2

  Paprsky se mají v bodě A složit do světlého červeného proužku, tedy do maxima. Pro interferenční maximum platí vztah:

  \[\mathrm{\Delta}l = k \lambda,\]

  kde λ je vlnová délka, k je řád maxima a platí, že k = 0, 1, 2, 3, ...

  V naší úloze máme počítat s prvním maximem, tedy k = 1.

  Podrobné odvození najdete v úloze Skládání světla.

• Nápověda 3

  Jak bude vypadat vztah pro vzdálenost prvního červeného maxima Δx, které vznikne na stínítku, pokud si jej vyjádříme pomocí úhlu odchýlení α?

• Řešení nápovědy 3

  Načrtněme si obrázek.

  

  Zde d je vzdálenost zdrojů od stínítka, α je úhel odchýlení, Δx je vzdálenost maxima 1. řádu červené barvy od maxima 0. řádu.

  Vzdálenost Δx si můžeme vyjádřit pomocí funkce tangens. Dostaneme:

  \[\mathrm{tg}\,\,\alpha=\, \frac{\mathrm{\Delta}x}{d} \quad\Rightarrow\quad \mathrm{\Delta}x=\,d\,\mathrm{tg}\,\,\alpha,\]

  kde za α si dosadíme vztah vyjádřený v předchozí nápovědě.

• Zápis

  b = 0,45 mm = 4,5·10−4 m	vzdálenost dvou zdrojů
  λ = 700 nm = 7,0·10−7 m	vlnová délka světla
  k = 1	řád maxima
  d = 0,5 m	vzdálenost stínítka od zdrojů
  Δx = ? (mm)	vzdálenost prvního maxima červené barvy od maxima 0. řádu

• Řešení

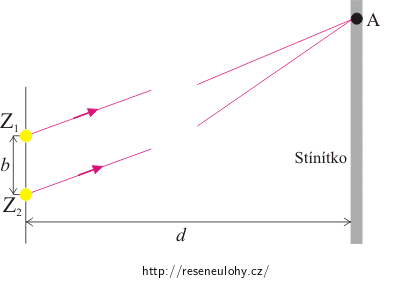
  Ze zdrojů se světlo šíří všemi směry. Světlo z obou zdrojů dopadá na stínítko a vzniká interferenční obrazec. Na stínítku vznikají maxima a minima, jejich polohy závisí na dráhovém rozdílu dvou paprsků vycházejících ze zdrojů.

  Předpokládejme, že stínítko je tak daleko od zdrojů, že paprsky přicházející do určitého bodu A stínítka jsou přibližně rovnoběžné.

  

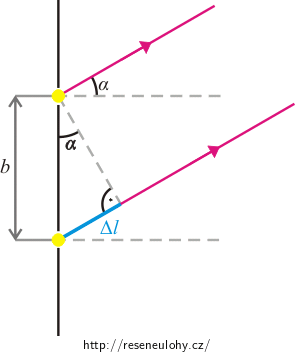
  Na obrázku z trojúhelníku získáme vztah pro dráhový rozdíl sousedních paprsků Δl:

  \[\mathrm{\Delta}l = \,b\sin\,\alpha,\]

  kde b je vzdálenost zdrojů a α je úhel, který paprsky svírají s centrální osou.

  Paprsky se v bodě A složily do světlého proužku, tedy do maxima, platí tedy pro dráhový rozdíl Δl:

  \[\mathrm{\Delta}l = k \lambda,\]

  kde k = 1. Z obou rovnic si vyjádříme sin α:

  \[\sin\,\alpha=\,\frac{\lambda}{b}.\]

   

  Nakreslíme si obrázek, kde označíme jako d vzdálenost zdrojů od stínítka, α úhel odchýlení, Δx vzdálenost maxima 1. řádu červené barvy od maxima 0. řádu.

  

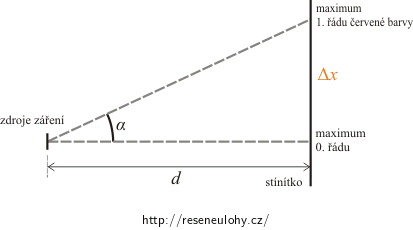
  Dostaneme:

  \[\mathrm{tg}\,\,\alpha=\, \frac{\mathrm{\Delta}x}{d} \quad\Rightarrow\quad \mathrm{\Delta}x=\,d\,\mathrm{tg}\,\,\alpha,\]

  kde α vypočítáme ze vztahu:

  \[\sin\,\alpha=\,\frac{\lambda}{b}=\,\frac{7{,}0{\cdot}10^{−7}}{4{,}5{\cdot}10^{−4}}\,\dot=\,0{,}00156 \quad\Rightarrow\quad \alpha\,\dot=\,0{,}00156,\]

  a dosadíme hodnoty ze zadání.

  \[\mathrm{\Delta}x=\,d\,\mathrm{tg}\,\,\alpha=\,0{,}5\,\cdot(\mathrm{tg}\,\,0{,}00156)\,\mathrm{m}\,\dot=\, 8{,}0{\cdot}10^{−4}\,\mathrm{m}\,\dot= \,0{,}80\,\mathrm{mm}. \]

   

  Poznámka k řešení:

  V řešení bychom pro zjednodušení výpočtu mohli použít zanedbání. Víme, že se jedná o velmi malé úhly, pro které platí

  \[\sin\,\alpha\ \dot{=}\ \, \alpha\ \dot{=}\ \mathrm{tg}\,\,\alpha,\]

  kde prostřední rovnost platí, pokud je uvažovaný úhel dosazen v radiánech.

  Výpočet nyní provedeme se zanedbáním.

   

  Vztah:

  \[\sin\,\alpha=\,\frac{\lambda}{b},\]

  si dosadíme do rovnice pro Δx:

  \[\mathrm{\Delta}x=\,d\,\mathrm{tg}\,\,\alpha=\,d\,\frac{\lambda}{b}.\]

  Dosadíme číselně.

  \[\mathrm{\Delta}x=\,d\,\frac{\lambda}{b}=\,0{,}5\cdot\,\frac{7{,}0{\cdot}10^{−7}}{4{,}5{\cdot}10^{−4}}\,\mathrm{m}\,\dot=\,7{,}8{\cdot}10^{−4}\,\mathrm{m}\,\dot=\,0{,}78\,\mathrm{mm}.\]

  Můžeme tedy vidět, že úlohu lze počítat se zanedbáním. Výsledky se od sebe příliš neliší.

• Odpověď

  První světlý pruh červené barvy se objeví přibližně 0,8 mm od nultého maxima.

• Odkaz na pokus

  Pokud vás zajímá, jak vypadá interferenční obrazec na stínítku ve skutečnosti, podívejte se na Dvojštěrbinový pokus.