Výpočet vrypů z odchýlení maxima
Úloha číslo: 1650
Kolik vrypů na 1 mm má optická mřížka, jestliže se světlo o vlnové délce 589,6 nm ve druhém maximu odchyluje od směru kolmého k rovině mřížky o úhel 43°15′?
Obrázek
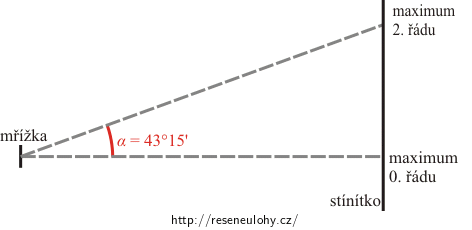
Na obrázku jsme si označili jako úhel α úhel odchýlení maxima 2. řádu od maxima 0. řádu.
Nápověda 1
Jak souvisí vzdálenost dvou vrypů na mřížce (tzv. mřížková konstanta) a počet vrypů na 1 mm mřížky?
Pokud si nejste jistí, podívejte se na řešení úlohy Výpočet vrypů na 1 mm.
Nápověda 2
Nalezněte vztah pro úhel odchýlení maxima 2. řádu a určete z něj mřížkovou konstantu.
Zápis
k = 2 řád maxima λ = 589,6 nm = 5,896·10−7 m vlnová délka dopadajícího světla α = 43°15′ úhel odchýlení maxima 2. řádu od nultého řádu N = ? počet vrypů na 1 mm Řešení
V úloze chceme spočítat, kolik má mřížka vrypů na 1 mm. K tomu potřebujeme najít mřížkovou konstantu b, což je vzdálenost dvou sousedních štěrbin mřížky. Počet vrypů N na 1 mm této mřížky je dán vztahem:
\[N=\,\frac{10^{-3}\,\mathrm{m}}{b}.\]Nakreslíme si obrázek situace a označíme si jako α úhel odchýlení maxima 2. řádu od maxima 0. řádu a polohy maxim.

Světlo procházející mřížkou se na mřížce ohýbá a na vzdáleném stínítku vzniká interferenční obrazec. Každé dva sousední paprsky mají dráhový rozdíl Δl, pro který platí:
\[\mathrm{Δ}l = \,b\sin\,α.\]Odtud si vyjádříme mřížkovou konstantu b a pro dráhový rozdíl Δl v případě maxima platí vztah Δl = kλ:
\[b=\,\frac{\mathrm{Δ}l}{\sin\,α}=\,\frac{kλ}{\sin\,α}.\]Nyní si dosadíme do rovnice pro počet vrypů N za mřížkovou konstantu b a vypočítáme:
\[N=\,\frac{10^{-3}\,\mathrm{m}}{\frac{kλ}{\sin\,α}}=\,\frac{10^{-3}\,\mathrm{m}\cdot\,\sin\,α}{kλ}=\,\frac{10^{-3}\,\mathrm{m}\cdot\,\sin\,43°15'}{\mathrm{2}\cdot\,5{,}896{\cdot}10^{-7}\,\mathrm{m}}\dot=\,581.\]Odpověď
Optická mřížka má 581 vrypů na 1 mm.




