Kulová vlna
Úloha číslo: 1400
Ukažte, že kulová vlna ve tvaru
\[ U(t,r) = \mathcal{U}_0 \frac{f\left(t-\frac{r}{c}\right)}{r}, \]kde \(\mathcal{U}_0\) je konstanta a \(r\) velikost polohového vektoru, je řešením vlnové rovnice \(\Delta U - \frac{1}{c^2} \frac{\partial ^2 U}{\partial t^2} = 0.\)
Nejčastěji se uvažuje vlna harmonická, kdy funkce \(f\) je goniometrická, zde ale počítejte s obecnou funkcí \(f\).
Rozbor
Pokud má být vlna řešením vlnové rovnice, musí po dosazení funkce \(U(r,t)\) do levé strany vlnové rovnice vyjít \(0\).
Potřebujeme tedy nejprve napočítat první a následně i druhou časovou derivaci funkce \(U(r,t)\) a také výsledek zapůsobení operátoru Laplace.
Nápověda 1 – první a druhá časová derivace
Určete první \(\frac{\partial U}{\partial t}\)a následně druhou \(\frac{\partial^2 U}{\partial t^2}\) časovou derivaci funkce \(U\).
Nápověda 2 – výpočet △U
Výsledek \(\Delta U\) určete pomocí vyjádření Laplaceova operátoru jako složení divergence a gradientu
\[\Delta U = \mathrm{div\,grad\,} U.\]Při výpočtu se budou hodit tyto identity a poznatky
- \( \mathrm{grad\,\psi(r)} = \vec{r}_0 \frac{\mathrm{d}\psi}{\mathrm{d}r}, \)
- \(\mathrm{div\,}\psi \vec{A} = \vec{A} \mathrm{grad\,} \psi + \psi \mathrm{div\,} \vec{A},\)
- \(\mathrm{div\,}\vec{r}_0 = \frac{2}{r}, \quad \mathrm{kde\,}\vec{r}_0 = \frac{\vec{r}}{\| \vec{r}\|}.\)
Nápověda 3 – dosazení do vlnové rovnice
Dosaďte nalezená vyjádření \(\frac{\partial^2 U}{\partial t^2}\) a \(\Delta U\) do vlnové rovnice a učiňte závěr.
CELKOVÉ ŘEŠENÍ
Pokud má být vlna řešením vlnové rovnice, musí po dosazení funkce \(U(r,t)\) do levé strany vlnové rovnice vyjít \(0\).
Potřebujeme tedy nejprve napočítat první a následně i druhou časovou derivaci funkce \(U(r,t)\) a také výsledek zapůsobení operátoru Laplace.
První časová derivace \(U\) je
\[ \frac{\partial U}{\partial t} = \frac{\mathcal{U}_0}{r}\frac{\partial f\left(t-\frac{r}{c}\right)}{\partial t} = \frac{\mathcal{U}_0}{r} f^\prime \cdot 1 = \frac{\mathcal{U}_0}{r} f^\prime. \]A druhá časová derivace pak
\[ \frac{\partial^2 U}{\partial t^2} = \frac{\partial }{\partial t} \left(\frac{\mathcal{U}_0}{r} f^\prime\right) = \frac{\mathcal{U}_0}{r} f^{\prime\prime} \cdot 1 = \frac{\mathcal{U}_0}{r} f^{\prime\prime}. \tag{1}\]Poznámka: Derivaci funkce podle své vnitřní funkce značíme čárkou.
Tj. pro \(f\left(g(t)\right)\) symbol \(f^\prime\) značí \(\frac{\mathrm{d}f}{\mathrm{d}g}\).
Výsledek \(\Delta U\) vypočítáme pomocí vyjádření \(\Delta U = \mathrm{div\,grad\,} U\).
Nejprve vypočítáme \(\mathrm{grad\,} U\). Užijeme identity \( \mathrm{grad\,\psi(r)} = \vec{r}_0 \frac{\mathrm{d}\psi}{\mathrm{d}r}\)
\[ \mathrm{grad\,} U = \mathcal{U}_0\, \mathrm{grad\,} \left[ \frac{f\left(t-\frac{r}{c}\right)}{r} \right]= \mathcal{U}_0 \vec{r_0} \frac{-\frac{1}{c}f^\prime r - f\cdot 1}{r^2}. \]Derivujeme-li funkci \(f\), nesmíme zapomínat na derivaci vnitřní funkce!
Abychom dostali \(\Delta U\), musíme na právě získaný výraz provést divergenci, tj.
\[ \mathrm{div\,grad\,}U = \mathcal{U}_0\, \mathrm{div\,} \left[ \vec{r_0} \frac{-\frac{1}{c}f^\prime r - f\cdot 1}{r^2}\right] = \]Užijeme identity \(\mathrm{div\,}\psi \vec{A} = \vec{A} \mathrm{grad\,} \psi + \psi \mathrm{div\,} \vec{A}\).
\[ =\mathcal{U}_0 \left[ \vec{r}_0 \mathrm{grad\,}\left( \frac{-\frac{1}{c}f^\prime r - f}{r^2}\right)+ \frac{-\frac{1}{c}f^\prime r - f}{r^2} \mathrm{div\,} \vec{r}_0 \right] = \]Opět použijeme identitu pro \(\mathrm{grad\,\psi(r)}\) a dále rovnost \(\mathrm{div\,}\vec{r}_0 = \frac{2}{r}\). Dostáváme
\[ =\mathcal{U}_0 \left[ \vec{r}_0 \cdot \vec{r}_0 \frac{-\frac{1}{c}\left[\left(\frac{rf^{\prime\prime}}{c} + f^\prime \right) + \frac{f^\prime}{c}\right]r^2 - \left( - \frac{f^\prime r}{c} - f\right) 2r}{r^4} + \frac{-\frac{f^\prime r}{c}- f}{r^2} \frac{2}{r} \right]= \]Po jednoduchých úpravách
\[ = \mathcal{U}_0\frac{\frac{rf^{\prime\prime}}{c^2} + \frac{2f^\prime}{c} + \frac{2f}{r} - \frac{2f^\prime}{c} - \frac{2f}{r}}{r^2} = \frac{\mathcal{U}_0 f^{\prime\prime}}{rc^2}. \tag{2}\]
Dosadíme-li konečná vyjádření (1), (2) do vlnové rovnice, získáme
\[ \Delta U - \frac{1}{c^2} \frac{\partial ^2 U}{\partial t^2} = \frac{\mathcal{U}_0 f^{\prime\prime}}{rc^2} - \frac{1}{c^2} \frac{\mathcal{U}_0}{r} f^{\prime\prime} = 0. \]Dosazením do levé strany vlnové rovnice jsme získali nulu.
Udaná funkce \(U(r,t)\) splňuje vlnovou rovnici a má tedy právo nazývati se kulovou vlnou.
Odpověď
Funkce \(U(r,t)\) vyhovuje vlnové rovnici.
Komentář – jak přijít na rovnici kulové vlny
Nejprve si zjednodušeně ukážeme, jak přijít na funkci \(U=U(r,t)\) v zadání, která popisuje kulovou vlnu.
Mějme bodový zdroj vlny. Jeho oscilace veličiny \(U\) můžeme obecně popsat
\[U_\mathrm{z}(t) = \mathcal{U}_0 f(t),\]kde \(\mathcal{U}_0\) je konstanta a \(f(t)\) funkce závisející na čase, obvykle např. \(\cos\omega t\).
U kulové vlny očekáváme sférickou symetrii, tj. ve všech místech vzdálených \(r\) od zdroje vyžadujeme stejnou hodnotu.
Do místa vzdáleného \(r\) od zdroje dorazí hodnota o \(\frac{r}{c}\) později, kde \(c\) je rychlost šíření vlny. Předpokládáme samozřejmě izotropní homogenní prostředí.
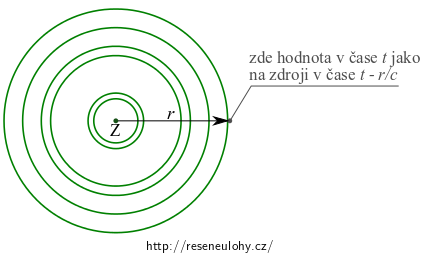
Pokud by byla funkce \(f\) harmonická, pak by byly vzdálenosti sousedních vlnoploch v obrázku stejné.
Hodnota veličiny \(U\) na sféře o poloměru \(r\) v čase \(t\) je stejná jako na zdroji v čase \(t-\frac{r}{c}\). Proto
\[U^\prime(r,t) = \mathcal{U}_0 f\left(t-\frac{r}{c}\right).\]Takto postavená vlna by si však s rostoucím \(r\) „držela“ amplitudu, což není z energetického hlediska možné. Přidáme proto ještě faktor \(\frac{1}{r}\), který představuje globální pokles amplitudy se vzdáleností od zdroje. Tedy konečně
\[U(r,t) = \mathcal{U}_0 \frac{f\left(t-\frac{r}{c}\right)}{r}.\]Proč zrovna faktor \(\textstyle \frac{1}{r}\)?
Veličina \(U\) může představovat například elektrickou intenzitu světla \(E\), či tlak vzduchu \(p\) při šíření zvuku. Intenzita \(I\) světla nebo zvuku je úměrná kvadrátu veličiny \(U\), zde tedy \(\frac{1}{r^2}\), což je přesně to, co očekáváme – intenzita kulového zdroje klesá s kvadrátem vzdálenosti. Tuto vlastnost lze zdůvodnit tím, že energie se s rostoucím poloměrem sféry \(r\) musí „rozšiřovat“ do plochy o obsahu, který roste s \(r^2\). Tj. energie připadající na jednotku obsahu nutně klesá s \(r^2\).


