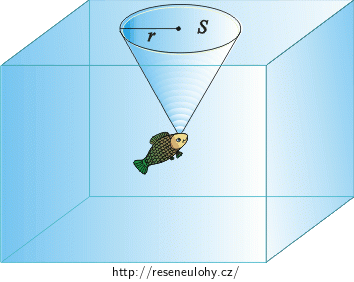
Na jak velké ploše vidí ryba oblohu?

Zápis

\(h=3\) \(\mathrm{m}\)	vzdálenost oka ryby od hladiny
\(S=\) \(?\)	plocha, na které ryba vidí oblohu

Nápověda 1

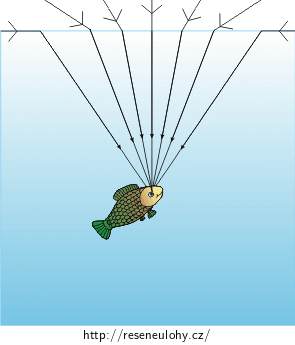
Nakreslete chod paprsků světla ze vzduchu k hladině a poté do oka ryby.

Řešení nápovědy 1

Paprsek dopadá na hladinu. Část paprsku se láme a dopadá do oka ryby a část se odráží od hladiny. Na obrázku jsou zakreslené jen některé paprsky, které dopadnou do oka. Ostatní paprsky, které dopadají do oka se nacházejí mezi zakreslenými paprsky.

Nápověda 2

Jaký tvar bude mít plocha, na které ryba uvidí oblohu?

Řešení nápovědy 2

Rybí oko bereme jako bod, do kterého se sbíhají paprsky.

Plocha bude mít tvar kruhu o poloměru \(r\): \[S=\pi · r^2.\tag{1}\]

Nápověda 3

V obrázku „Chod paprsků“, který se nachází v části „Řešení nápovědy \(1\)“, necháme zakreslené jen paprsky, které se lámou do oka.

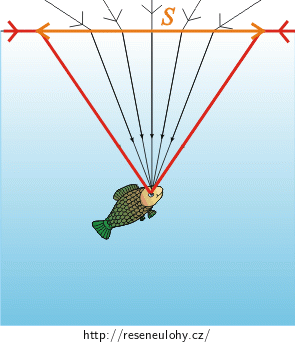
V obrázku vyznačte paprsky, které spolu svírají největší úhel. Tyto paprsky ohraničují hledanou plochu \(S\). Zdůvodněte.

Řešení nápovědy 3

Paprsky, které svírají největší úhel jsou vyznačeny červeně. Hledaná plocha \(S\) je vyznačena oranžově.

Na hledanou plochu na hladině dopadají z oblohy paprsky, které se pak lámou do oka ryby a díky nim vidí ryba oblohu.

Paprsek nemůže dopadat na hladinu pod větším úhlem než je \(90°.\)

Další paprsky, co by mohly dopadnout do oka ryby by musely vycházet z míst pod hladinou, ale tyto paprsky nás nezajímají (rybě by tyto paprsky nepomohly k tomu, aby viděla oblohu).

Nápověda 4

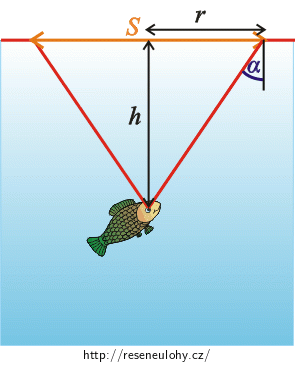
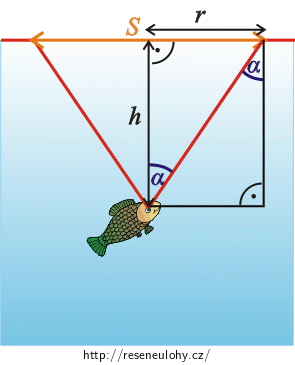
Zaměříme se nyní pouze na paprsky, které se lámou pod úhlem \(\mathrm{α}\) viz „Obrázek k nápovědě \(4\)“.

V obrázku vyznačíme poloměr hledané plochy \(r\) a vzdálenost oka ryby od hladiny \(h\).

1) Ze zákona lomu napište vztah pro úhel \(\mathrm{α}\).

2) Z obrázku odvoďte, jaký je vztah mezi \(\mathrm{α}\), \(r\) a \(h\).

Řešení nápovědy 4

1) Ze Snellova zákona odvodíme vztah pro úhel lomu: \[\frac{\sin {90°}}{\sin \mathrm{α}}=\frac{n_{2}}{n_{1}},\] kde \(n_{1}\) je index lomu vzduchu a \(n_{2}\) je index lomu vody.

Protože \(\sin {90°}=1\), můžeme napsat:

\[\frac{1}{\sin \mathrm{α}}=\frac{n_{2}}{n_{1}},\]

Odtud vyjádříme \(\sin \mathrm{α}\):

\[\sin \mathrm{α}=\frac{n_{1}}{n_{2}},\tag{2}\]

2) Díky podobnosti trojúhelníků můžeme obrázek upravit následovně:

Z obrázku vidíme, že platí \[\sin \mathrm{α}=\frac{r}{\sqrt{r^2+h^2}},\tag{3}\] kde \(\sqrt{r^2+h^2}\) je přepona trojúhelníku, jejíž velikost jsme určili z Pythagorovy věty.

Nápověda 5

Ze vztahu (3) vyjádřete poloměr \(r\) a pomocí vztahu získaného ze zákona lomu (2), upravte získaný vzorec tak, aby \(r\) závisel pouze na \(h\), \(n_{1}\) a \(n_{2}\).

Následně dosaďte za \(r\) do vztahu pro výpočet plochy kruhu (1) a číselně dopočítejte velikost hledané plochy.

Řešení nápovědy 5

(1): \(S=\pi · r^2,\)

(2): \(\sin \mathrm{α}=\frac{n_{1}}{n_{2}},\)

(3): \(\sin \mathrm{α}=\frac{r}{\sqrt{r^2+h^2}}.\)

Obě strany rovnice (3) vynásobíme \(\sqrt{r^2+h^2}\) a dostaneme: \[r=\sqrt{r^2+h^2}·\sin \mathrm{α}.\]

Dle (2) dosadíme za \(\sin \mathrm{α}\): \[r= \sqrt{r^2+h^2} · \frac{n_{1}}{n_{2}}.\]

Obě strany rovnice umocníme a roznásobíme závorku:

\[r^2= \left(r^2+h^2 \right)· \left(\frac{n_{1}}{n_{2}}\right)^2=r^2\left(\frac{n_{1}}{n_{2}}\right)^2+h^2\left(\frac{n_{1}}{n_{2}}\right)^2 .\]

Od obou stran rovnice odečteme \(r^2\left (\frac{n_{1}}{n_{2}}\right )^2\) a \(r^2\) vytkneme: \[r^2\left [1 − \left(\frac{n_{1}}{n_{2}}\right)^2\right]= h^2\left (\frac{n_{1}}{n_{2}}\right)^2 .\]

Obě strany rovnice vydělíme \(\left[1 − (\frac{n_{1}}{n_{2}})^2\right]\) a odmocníme: \[r= \frac {h\left(\frac{n_{1}}{n_{2}}\right)} {\sqrt{1 − \left(\frac{n_{1}}{n_{2}}\right)^2}}= \frac {h · n_{1}} {n_{2} \sqrt{1 − \left(\frac{n_{1}}{n_{2}}\right)^2}} .\]

Převedeme vztah pod odmocninou na společného jmenovatele a zlomek upravíme: \[r= \frac {h · n_{1}} {n_{2} \sqrt{\frac{n_{2}^2−n_{1}^2}{n_{2}^2}}} =\frac {h · n_{1}} { \sqrt{n_{2}^2−n_{1}^2}}.\]

Dosadíme za \(r\) do vztahu (1) a vztah umocníme: \[S=\pi r^2=\pi · \left( \frac {h · n_{1}} {\sqrt{n_{2}^2−n_{1}^2}}\right)^2= \pi · \frac {h^2 · n_{1}^2} {n_{2}^2−n_{1}^2} .\]

Číselné řešení:

Ze zadání víme:

\(h=3\) \(\mathrm{m}\).

V tabulkách dohledáme hodnoty pro \(\pi\), \(n_{2}\) a \(n_{1}\):

Ludolfovo číslo			\(\pi\) \(\dot=\) \(3{,}14\)
Index lomu vzduchu			\(n_{1}\) \(\dot=\) \(1{,}00\)
Index lomu vody			\(n_{2}\) \(\dot=\) \(1{,}33\)

Dosadíme a dostáváme velikost hledané plochy:

\(S\) \(\dot=\) \(\frac{3{,}14 · 3^2 ·{1{,}00}^2}{{1{,}33}^2 − {1{,}00}^2}\) \(\mathrm{m^2}=\frac{3{,}14 · 9 ·1}{{1{,}33}^2 − {1}}\) \(\mathrm{m^2}\) \(\dot=\) \(36{,}8\) \(\mathrm{m^2}.\)

A jejího poloměru:

\(r\) \(\dot=\) \( \frac {3 · 1{,}00} {\sqrt{1{,}33^2 −1{,}00^2}}\) \(\mathrm{m}\) \(=\) \( \frac {3} {\sqrt{1{,}33^2 − 1}}\) \(\mathrm{m}\) \(\dot=\) \(3{,}42\) \(\mathrm{m}\).

Celkové řešení

Chod paprsků světla a tvar plochy, na které ryba vidí oblohu