Hmotný bod v různých souřadnicích
Úloha číslo: 1236
Nalezněte Lagrangeovu a Hamiltonovu funkci, Lagrangeovy rovnice II. druhu a Hamiltonovy kanonické rovnice pro hmotný bod pohybující se v časově neproměnném silovém poli s potenciální energií \(V(\vec{r})\)
- v kartézských souřadnicích,
- ve válcových souřadnicích,
- ve sférických souřadnicích.
Nápověda – přehled vzorců
Lagrangeovu funkci L spočteme jako:
\[L=T-V.\]Lagrangeovy rovnice II. druhu mají obecně tvar:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{q_i}}}\right)-\frac{\partial{L}}{\partial{q_i}}=0,\]kde qi jsou zobecněné souřadnice a \(\dot{q_i}\) zobecněné rychlosti.
Pomocí Lagrangeovy funkce může spočítat také zobecněné hybnosti pi vztahem:
\[p_i=\frac{\partial{L}}{\partial{\dot{q_i}}}.\]Hamiltonova funkce H je definována obecně jako:
\[H=\sum_{i=1}^n{p_i\dot{q_i}}-L,\]kde pi je složka zobecněné hybnosti a qi je příslušná zobecněná souřadnice. Vyjadřujeme ji v jejích přirozených proměnných, kterými jsou právě zobecněné souřadnice a hybnosti.
V případě, že není lagrangián explicitně závislý na čase, lze hamiltonián vypočítat jako celkovou energii systému:
\[H=T+V.\]Hamiltonovy kanonické rovnice mají tvar:
\[\dot{q_i}=\frac{\partial{H}}{\partial{p_i}},\] \[\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}}.\]Nápověda – křivočaré souřadnice
Křivočaré souřadnice (v našem případě válcové a sférické) můžeme vyjádřit pomocí kartézských souřadnic x, y a z.
Pro válcové souřadnice r, ϑ a z platí vyjádření:
\[x=r\cos{\vartheta},\] \[y=r\sin{\vartheta},\] \[z=z.\]Ve sférický souřadnicích můžeme vyjádřit kartézské souřadnice pomocí souřadnic r, ϑ a ψ jako:
\[x=r\sin{\vartheta}\cos{\psi},\] \[y=r\sin{\vartheta}\sin{\psi},\] \[z=r\cos{\vartheta}.\]Tato vyjádření dosaďte za kartézské souřadnice do vztahů pro kinetickou a potenciální energii a pokračujte ve výpočtech jako u kartézských souřadnic.
a) Lagrangián a Lagrangeovy rovnice II. druhu
Potenciální energie V je obecně funkcí všech kartézských souřadnic:
\[V=V(\vec{r})=V(x,y,z).\]Kinetická energie T má tvar:
\[T=\frac{1}{2}m(\dot{x}^2+\dot{y}^2+\dot{z}^2).\]Lagrangeova funkci L tedy můžeme sestrojit jako:
\[L=T-V=\frac{1}{2}m(\dot{x}^2+\dot{y}^2+\dot{z}^2)-V(x,y,z).\]Pomocí lagrangiánu můžeme napsat Lagrangeovy rovnice druhého druhu:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)-\frac{\partial{L}}{\partial{x}}=0,\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{y}}}\right)-\frac{\partial{L}}{\partial{y}}=0,\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{z}}}\right)-\frac{\partial{L}}{\partial{z}}=0.\]Jak vidíme, potenciální energie V, která se nachází v lagrangiánu L, je funkcí zobecněných souřadnic, nikoliv však rychlostí. Proto při derivacích podle zobecněných rychlostí \(\dot{x}, \dot{y}, \dot{z} \) tento člen vypadne. Naopak kinetická energie T není závislá na zobecněných souřadnicích. Rovnice tak můžeme přepsat do tvaru:
\[m\ddot{x}=-\frac{\partial{V}}{\partial{x}},\] \[m\ddot{y}=-\frac{\partial{V}}{\partial{y}},\] \[m\ddot{z}=-\frac{\partial{V}}{\partial{z}}.\]Můžeme si všimnout, že na pravých stranách rovnic vystupují složky síly. Jedná se tedy o Newtonovy pohybové rovnice.
a) Hamiltonián a Hamiltonovy kanonické rovnice
V minulé sekci jsme zjistili, že lagrangián L není explicitně závislý na čase. V takovém případě nebude časově závislý ani hamiltonián H, který tak můžeme vyjádřit jako celkovou energii systému:
\[H=T+V.\]Přirozené proměnné hamiltoniánu H jsou zobecněné souřadnice a hybnosti. Bude se nám tedy hodit, budeme-li znát jejich vyjádření.
Zobecněnými souřadnicemi jsou přímo kartézské souřadnice x, y a z. Zobecněné hybnosti budou mít tedy tvar hybností, které známe z klasické mechaniky:
\[p_x=\frac{\partial{L}}{\partial{\dot{x}}}=m\dot{x},\] \[p_y=\frac{\partial{L}}{\partial{\dot{y}}}=m\dot{y},\] \[p_z=\frac{\partial{L}}{\partial{\dot{z}}}=m\dot{z}.\]Nyní již můžeme do hamiltoniánu H dosadit a vyjádřit výsledek pomocí přirozených proměnných:
\[H=T+V=\frac{1}{2m}(p_x^2+p_y^2+p_z^2)+V(x,y,z).\]Hamiltonovy kanonické rovnice nabývají v našem případě tvaru:
První série:
\[\dot{x}=\frac{\partial{H}}{\partial{p_x}}=\frac{p_x}{m},\] \[\dot{y}=\frac{\partial{H}}{\partial{p_y}}=\frac{p_y}{m},\] \[\dot{z}=\frac{\partial{H}}{\partial{p_z}}=\frac{p_z}{m}.\]Druhá série:
\[\dot{p_x}=-\frac{\partial{H}}{\partial{x}}=-\frac{\partial{V}}{\partial{x}}\] \[\dot{p_y}=-\frac{\partial{H}}{\partial{y}}=-\frac{\partial{V}}{\partial{y}},\] \[\dot{p_z}=-\frac{\partial{H}}{\partial{z}}=-\frac{\partial{V}}{\partial{z}}.\]Derivujeme-li Hamiltonovu funkci podle souřadnic, bude derivace první části, která odpovídá v hamiltoniánu kinetické energii T, vždy rovna nule (kinetická energie nezávisí na souřadnicích) a v rovnicích místo hamiltoniánu H zůstane pouze potenciální energie V.
Jako pohybové rovnice jsem získali soustavu šesti diferenicálních rovnic prvního řádu. Pomocí Lagrangeova formalismu jsme získali tři diferenciální rovnice druhého řádu. Tyto rovnice je na sebe možno navzájem převést, což činíme.
Aby soustava mohla nabýt tvaru Newtonových pohybových rovnic, musíme do nich dosadit za složky hybnosti. Dostáváme:
\[m\ddot{x}=-\frac{\partial{V}}{\partial{x}},\] \[m\ddot{y}=-\frac{\partial{V}}{\partial{y}},\] \[m\ddot{z}=-\frac{\partial{V}}{\partial{z}}.\]Získali jsme tak Newtonovy pohybové rovnice, které můžeme řešit. Stejné rovnice jsme získali pomocí Lagrangeových rovnic II. druhu v předchozím oddílu.
b) Lagrangián a Lagrangeovy rovnice II. druhu
Potenciální energie V je funkcí všech válcových souřadnic:
\[V=V(r,\vartheta,z).\]Kinetická energie T má v kartézských souřadnicích tvar:
\[T=\frac{1}{2}m(\dot{x}^2+\dot{y}^2+\dot{z}^2).\]Za kartézské souřadnice dosadíme vyjádření ve válcových souřadnicích:
\[x=r\cos{\vartheta},\] \[y=r\sin{\vartheta},\] \[z=z.\]V dalším postupu se nám bude hodit, budeme-li znát časové derivace těchto souřadnic:
\[\dot{x}=\dot{r}\cos{\vartheta}-r\dot{\vartheta}\sin{\vartheta},\] \[\dot{y}=\dot{r}\sin{\vartheta}+r\dot{\vartheta}\cos{\vartheta},\] \[\dot{z}=\dot{z}.\]Dosadíme do vyjádření kinetické energie T:
\[T=\frac{1}{2}m \left[(\dot{r}\cos{\vartheta}-r\dot{\vartheta}\sin{\vartheta})^2+(\dot{r}\sin{\vartheta}+r\dot{\vartheta}\cos{\vartheta})^2+\dot{z}^2 \right],\]roznásobíme závorky:
\[T=\frac{1}{2}m \left[\dot{r}^2\cos^2{\vartheta}-2r\dot{r}\dot{\vartheta}\cos{\vartheta}\sin{\vartheta}+r^2\dot{\vartheta}^2\sin^2{\vartheta}+\dot{r}^2\sin^2{\vartheta}+2r\dot{r}\dot{\vartheta}\cos{\vartheta}\sin{\vartheta}+r^2\dot{\vartheta}^2\cos^2{\vartheta}+\dot{z}^2 \right],\]a upravíme:
\[T=\frac{1}{2}m \left[\dot{r}^2(\sin^2{\vartheta}+\cos^2{\vartheta})+r^2\dot{\vartheta}^2(\sin^2{\vartheta}+\cos^2{\vartheta})+\dot{z}^2 \right]=\frac{1}{2}m(\dot{r}^2+r^2\dot{\vartheta}^2+\dot{z}^2).\]K tomuto výrazu se dá dospět ještě dalším způsobem. Ten naleznete v komentáři na konci úlohy.
Nyní můžeme napsat Lagrangeovu funkci L:
\[L=T-V=\frac{1}{2}m(\dot{r}^2+r^2\dot{\vartheta}^2+\dot{z}^2)-V(r,\vartheta,z).\]Pomocí lagrangiánu můžeme napsat Lagrangeovy rovnice druhého druhu ve tvaru:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{r}}}\right)-\frac{\partial{L}}{\partial{r}}=0,\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{\vartheta}}}\right)-\frac{\partial{L}}{\partial{\vartheta}}=0,\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{z}}}\right)-\frac{\partial{L}}{\partial{z}}=0.\]Stejně jako u kartézských souřadnic, potenciální energie V je funkcí zobecněných souřadnic, nikoliv však rychlostí. Proto při derivacích podle zobecněných rychlostí \(\dot{r}, \dot{\vartheta}, \dot{z} \) tento člen vypadne. Rovnice tak můžeme přepsat do tvaru:
\[\frac{\mathrm{d}}{\mathrm{d}t}(m\dot{r})=-\frac{\partial{V}}{\partial{r}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(mr^2\dot{\vartheta})=-\frac{\partial{V}}{\partial{\vartheta}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(m\dot{z})=-\frac{\partial{V}}{\partial{z}}.\]b) Hamiltonián a Hamiltonovy kanonické rovnice
Lagrangián L není explicitně závislý na čase, proto se hamiltonián H rovná celkové energii systému:
\[H=T+V.\]Přirozené proměnné hamiltoniánu H jsou zobecněné souřadnice a hybnosti. Bude se nám tedy hodit, budeme-li znát jejich vyjádření.
Zobecněné hybnosti můžeme spočítat z lagrangiánu podle vzorce:
\[p_i=\frac{\partial{L}}{\partial{\dot{q_i}}}.\]Konkrétně:
\[p_r=\frac{\partial{L}}{\partial{\dot{r}}}=m\dot{r} => \dot{r}=\frac{p_r}{m},\] \[p_{\vartheta}=\frac{\partial{L}}{\partial{\dot{\vartheta}}}=mr^2\dot{\vartheta} => \dot{\vartheta}=\frac{p_{\vartheta}}{mr^2},\] \[p_z=\frac{\partial{L}}{\partial{\dot{z}}}=m\dot{z} => \dot{z}=\frac{p_z}{m}.\]Nyní již můžeme pomocí zobecněných hybností vyjádřit hamiltonián:
\[H=T+V=\frac{1}{2m}\left(p_r^2+\frac{1}{r^2}p_{\vartheta}^2+p_z^2\right)+V(r,\vartheta,z)\]Hamiltonovy kanonické rovnice nabývají v našem případě tvaru:
První série:
\[\dot{r}=\frac{\partial{H}}{\partial{p_r}}=\frac{p_r}{m},\] \[\dot{\vartheta}=\frac{\partial{H}}{\partial{p_{\vartheta}}}=\frac{p_\vartheta}{mr^2},\] \[\dot{z}=\frac{\partial{H}}{\partial{p_z}}=\frac{p_z}{m}.\]Druhá série:
\[\dot{p_r}=-\frac{\partial{V}}{\partial{r}},\] \[\dot{p_{\vartheta}}=-\frac{\partial{V}}{\partial{\vartheta}},\] \[\dot{p_z}=-\frac{\partial{V}}{\partial{z}}.\]Dostali jsme pohybové rovnice jako soustavu šesti tentokrát nelineárních rovnic prvního řádu. Abychom ukázali, že lze tyto rovnice převést na tři diferenciální rovnice druhého řádu, které jsme dostali pomocí Lagrangeových rovnic, dosadíme za složky hybnosti:
\[\frac{\mathrm{d}}{\mathrm{d}t}(m\dot{r})=-\frac{\partial{V}}{\partial{r}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(mr^2\dot{\vartheta})=-\frac{\partial{V}}{\partial{\vartheta}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(m\dot{z})=-\frac{\partial{V}}{\partial{z}}.\]Jak vidíme, rovnice si skutečně odpovídají s Lagrangeovými rovnicemi II. druhu. Navíc se jedná o Newtonovy pohybové rovnice, což zjistíme, pokud si uvědomíme, že na pravých stranách vystupují složky vektoru síly.
c) Lagrangián a Lagrangeovy rovnice II. druhu
Potenciální energie V je funkcí všech sférických souřadnic:
\[V=V(r,\vartheta,\psi).\]Kinetická energie T má tvar:
\[T=\frac{1}{2}m(\dot{r}^2+r^2\dot{\vartheta}^2+r^2\sin^2{\vartheta}\ \dot{\psi}^2).\]Pozn.: K tomuto tvaru dospějeme, pokud dosadíme do kinetické energie T v kartézský souřadnicích x, y a z právě za tyto souřadnice jejich vyjádření ve sférických souřadnicích (viz nápověda křivočaré souřadnice). Obdobné dosazení bylo provedeno v minulé sekci pro válcové souřadnice. Uvedeme alespoň vyjádření derivací souřadnic, jejich dosazení a úpravu již necháme na čtenáři:
\[\dot{x}=\dot{r}\sin{\vartheta}\cos{\psi}+r\dot{\vartheta}\cos{\vartheta}\cos{\psi}-r\dot{\psi}\sin{\vartheta}\sin{\psi},\] \[\dot{y}=\dot{r}\sin{\vartheta}\sin{\psi}+r\dot{\vartheta}\cos{\vartheta}\sin{\psi}+r\dot{\psi}\sin{\vartheta}\cos{\psi},\] \[\dot{z}=\dot{r}\cos{\vartheta}-r\dot{\vartheta}\sin{\vartheta}.\]Nyní můžeme napsat Lagrangeovu funkci L:
\[L=T-V=\frac{1}{2}m(\dot{r}^2+r^2\dot{\vartheta}^2+r^2\sin^2{\vartheta}\ \dot{\psi}^2)-V(r,\vartheta,\psi).\]Pomocí lagrangiánu můžeme napsat Lagrangeovy rovnice druhého druhu ve tvaru:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{r}}}\right)-\frac{\partial{L}}{\partial{r}}=0,\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{\vartheta}}}\right)-\frac{\partial{L}}{\partial{\vartheta}}=0,\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{\psi}}}\right)-\frac{\partial{L}}{\partial{\psi}}=0.\]Potenciální energie V při derivacích podle zobecněných rychlostí \(\dot{r}, \dot{\vartheta}, \dot{\psi} \) vypadne. Rovnice tak můžeme přepsat do tvaru:
\[\frac{\mathrm{d}}{\mathrm{d}t}(m\dot{r})=\frac{\partial{L}}{\partial{r}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(mr^2\dot{\vartheta})=\frac{\partial{L}}{\partial{\vartheta}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(mr^2\sin^2{\vartheta}\ \dot{\psi})=\frac{\partial{L}}{\partial{\psi}}.\]Provedeme naznačené derivace a dostáváme:
\[m\ddot{r}=mr\dot{\vartheta}^2+mr\sin^2{\vartheta}\ \dot{\psi}^2-\frac{\partial{V}}{\partial{r}},\] \[2mr\dot{r}\dot{\vartheta}+mr^2\ddot{\vartheta}=mr^2\dot{\psi}^2\sin{\vartheta}\cos{\vartheta}-\frac{\partial{V}}{\partial{\vartheta}},\] \[2mr\dot{r}\dot{\psi}\sin^2{\vartheta}+2mr^2\dot{\vartheta}\ \dot{\psi}\sin{\vartheta}\cos{\vartheta}+mr^2\ddot{\psi}\sin^2{\vartheta}=-\frac{\partial{V}}{\partial{\psi}}.\]c) Hamiltonián a Hamiltonovy kanonické rovnice
Lagrangián L není explicitně závislý na čase, a proto hamiltonián H můžeme vyjádřit jako celkovou energii systému:
\[H=T+V.\]Přirozené proměnné hamiltoniánu H jsou zobecněné souřadnice a hybnosti.
Zobecněné hybnosti můžeme spočítat z lagrangiánu podle vzorce:
\[p_i=\frac{\partial{L}}{\partial{\dot{q_i}}}.\]Konkrétně:
\[p_r=\frac{\partial{L}}{\partial{\dot{r}}}=m\dot{r}\ =>\ \dot{r}=\frac{p_r}{m},\] \[p_{\vartheta}=\frac{\partial{L}}{\partial{\dot{\vartheta}}}=mr^2\dot{\vartheta}\ =>\ \dot{\vartheta}=\frac{p_{\vartheta}}{mr^2},\] \[p_{\psi}=\frac{\partial{L}}{\partial{\dot{\psi}}}=mr^2\sin^2{\vartheta}\dot{\psi}\ =>\ \dot{\psi}=\frac{p_{\psi}}{mr^2\sin^2{\vartheta}}.\]Nyní již můžeme pomocí zobecněných hybností vyjádřit hamiltonián:
\[H=T+V=\frac{1}{2m}\left(p_r^2+\frac{1}{r^2}p_{\vartheta}^2+\frac{1}{r^2\sin^2{\vartheta}}p_{\psi}^2\right)+V(r,\vartheta,z)\]Hamiltonovy kanonické rovnice nabývají v našem případě tvaru:
První série:
\[\dot{r}=\frac{\partial{H}}{\partial{p_r}}=\frac{p_r}{m},\] \[\dot{\vartheta}=\frac{\partial{H}}{\partial{p_{\vartheta}}}=\frac{p_\vartheta}{mr^2},\] \[\dot{\psi}=\frac{\partial{H}}{\partial{p_{\psi}}}=\frac{1}{mr^2\sin^2{\vartheta}}p_{\psi}.\]Druhá série:
\[\dot{p_r}=-\frac{\partial{H}}{\partial{r}},\] \[\dot{p_{\vartheta}}=-\frac{\partial{H}}{\partial{\vartheta}},\] \[\dot{p_{\psi}}=-\frac{\partial{H}}{\partial{\psi}}.\]Máme pohybové rovnice jako soustavu šesti nelineárních rovnic prvního řádu. Abychom předvedli, že je tyto rovnice možné převést na tři diferenciální rovnice druhého řádu (ty, které jsme dostali pomocí Lagrangeových rovnic), dosadíme za složky hybnosti:
\[\frac{\mathrm{d}}{\mathrm{d}t}(m\dot{r})=-\frac{\partial{H}}{\partial{r}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(mr^2\dot{\vartheta})=-\frac{\partial{H}}{\partial{\vartheta}},\] \[\frac{\mathrm{d}}{\mathrm{d}t}(mr^2\sin^2{\vartheta}\dot{\psi})=-\frac{\partial{H}}{\partial{\psi}}.\]Spočteme derivace a dosadíme za zobecněné hybnosti:
\[m\ddot{r}=mr\dot{\vartheta}^2+mr\sin^2{\vartheta}\ \dot{\psi}^2-\frac{\partial{V}}{\partial{r}},\] \[2mr\dot{r}\dot{\vartheta}+mr^2\ddot{\vartheta}=mr^2\dot{\psi}^2\sin{\vartheta}\cos{\vartheta}-\frac{\partial{V}}{\partial{\vartheta}},\] \[2mr\dot{r}\dot{\psi}\sin^2{\vartheta}+2mr^2\dot{\vartheta}\ \dot{\psi}\sin{\vartheta}\cos{\vartheta}+mr^2\ddot{\psi}\sin^2{\vartheta}=-\frac{\partial{V}}{\partial{\psi}}.\]Rovnice odpovídají těm, které jsme dostali pomocí Lagrangeova formalismu. Jedná se o Newtonovy pohybové rovnice – na pravých stranách vystupují složky vektoru síly.
Shrnutí – ekvivalence rovnic
Lagrangovy rovnice II. druhu jsou v našem případě (tj. pohyb jednoho hmotného bodu v třídimenzionálním prostoru) soustava tří rovnic druhého řádu a Hamiltonovy kanonické rovnice jsou soustava šesti rovnic prvního řádu. Ve všech třech případech (pro kartézské, válcové a sférické souřadnice) jsme ukázali jejich ekvivalenci. Pouze pro kartézské souřadnice rovnice mohou být lineární (záleží na průběhu potenciální energie), což usnadňuje jejich řešení.
Jakou soustavu souřadnic zvolíme pro řešení dané úlohy, je vhodné rozhodnout podle tvaru potenciální energie V. Kinetická energie T je sice nejjednodušší v kartézských souřadnicích, ale třeba pro sféricky symetrické pole je celkově jednodušší použít složitější vyjádření kinetické energie T ve sférických souřadnicích (v porovnání s kartézskými souřadnicemi), než komplikovaně vyjadřovat V v kartézských souřadnicích.
Kinetická energie v křivočarých souřadnicích
Válcové i sférické souřadnice jsou lokálně ortogonální, tj. v každém bodě jsou vektory, které určují přírůstky zobecněných souřadnic, na sebe kolmé. Ověření této skutečnosti naleznete v úlohách Diferenciální operátory ve válcových souřadnicích a Diferenciální operátory ve sférických souřadnicích.
Chceme-li spočítat velikost rychlosti částice v kartézských souřadnicích, můžeme využít jejich ortogonality a velkost vektoru rychlosti spočítat pomocí složek:
\[v=\sqrt{\dot{x}^2+\dot{y}^2+\dot{z}^2}.\]Díky lokální ortogonalitě můžeme ve válcových souřadnicích postupovat obdobně. Představte si, že se hmotný bod pohybuje tak, že se mění pouze jedna jeho souřadnice a zbylé dvě zůstávají konstantní, a uvažujte, čemu se rovná časová derivace dané souřadnice.
Časová derivace souřadnice r je rovna rychlosti v radiálním směru, časová derivace z je stejně jako v kartézských souřadnicích složka rychlosti ve svislém směru a časová derivace souřadnice ϑ je vlastně velikost úhlové rychlosti, kterou musíme převést na obvodovou rychlost vynásobením poloměrem kružnice, po které se hmotný bod pohybuje, tedy vynásobením r. Tyto tři složky rychlosti jsou na sebe kolmé, proto pro velikost rychlosti platí:
\[v=\sqrt{\dot{r}^2+r^2\dot{\vartheta}^2+\dot{z}^2}.\]Kinetickou energii hmotného bodu ve válcových souřadnicích dostáváme ve tvaru:
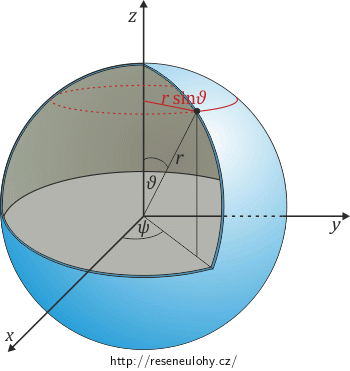
\[T=\frac{1}{2}m(\dot{r}^2+r^2\dot{\vartheta}^2+\dot{z}^2).\]Ve sférických souřadnicích r, ϑ a ψ je situace obdobná jako v souřadnicích válcových, změna je pouze ve třetí souřadnici ψ. Derivace souřadnice ψ je také úhlová rychlost. Opět je vhodné si představit pohyb, který se děje pouze v této souřadnici a zbylé dvě souřadnice jsou konstantní. Tímto pohybem je pohyb po kružnici s poloměrem \(r \sin{\vartheta}\), kterým úhlovou rychlost \(\dot{\psi}\) vynásobíme, a dostaneme příslušnou obvodovou rychlost. Pro velikost celkové rychlosti tak díky vzájemné kolmosti jednotlivých složek platí:
\[v=\sqrt{\dot{r}^2+r^2\dot{\vartheta}^2+r^2\sin^2{\vartheta}\dot{\psi}^2}.\]Kinetická energie hmotného bodu tak nabývá tvaru:
\[T=\frac{1}{2}m(\dot{r}^2+r^2\dot{\vartheta}^2+r^2\sin^2{\vartheta}\ \dot{\psi}^2).\]