Kulička v elektrostatickém a gravitačním poli
Úloha číslo: 710
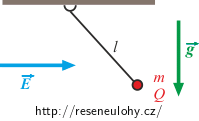
Závaží kyvadla o délce l je zavěšeno v homogenním gravitačním a elektrostatickém poli. Vektory intenzity elektrického pole \(\vec{E}\) a tíhového zrychlení \(\vec{g}\) jsou na sebe kolmé (viz náčrtek). Závaží můžeme považovat za hmotný bod o hmotnosti m a náboji q, vlákno je nehmotné. V jaké poloze se kyvadlo ustálí? Řešte pomocí zobecněného principu virtuální práce.
Připomenutí důležitých vzorců
Tíhovou sílu určíme snadno při znalosti hmotnosti hmotného bodu a tíhového zrychlení:
\[\vec{F}_g = m\vec{g}\ .\]Elektrostatickou sílu určíme rovněž jednoduše pomocí vektoru intenzity elektrického pole a náboje závaží kyvadla:
\[\vec{F}_e = q\vec{E}\ .\]Matematický vztah vystihující zobecněný princip virtuální práce (resp. princip virtuálních posunutí) je tento:
\[\sum_{i=1}^{N} \vec{F}_i \cdot \delta \vec{r}_i = 0\ ,\tag{*}\]tj. posčítáme-li skalární součiny celkové aktivní síly působící na i-tý hmotný bod a infinitezimálně malého vratného virruálního posunutí slučitelného s vazbami tohoto bodu přes všechny body, dostaneme nulu. \(\vec{F}_i\) je výslednice aktivních sil působící na i-tý hmotný bod, \(\delta \vec{r}_i\) je vektor nekonečně malého posunutí slučitelného s vazbami i-tého hmotného bodu.
Nápověda 1
Kolik budeme potřebovat parametrů k popisu pohybu kyvadla? Kolik má stupňů volnosti?
Nápověda 2
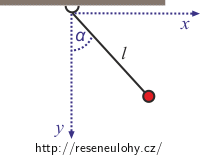
Pomocí úhlu α, který svírá závěs kyvadla s kolmou osou, parametrizujte polohu kyvadla. Možností jak to provést je pochopitelně velmi mnoho. Zvolme například počátek kartézských souřadnic v místě uchycení kyvadla a orientujme osu y dolů, stejně jako gravitační zrychlení, osa x míří ve směru intenzity elektrického pole.
Nápověda 3
Složky vektoru virtuálního, vratného, nekonečně malého posunutí dostaneme, když budeme diferencovat rovnice (1) popisující polohu kyvadla:
\[x = l \sin \alpha\tag{1}\] \[y = l \cos \alpha \ .\]Nápověda 4
Zapište obě působící aktivní síly jako vektory. Obecně by bylo potřeba je vyjádřit s pomocí parametru α, ovšem v této úloze jsou obě na poloze kuličky nezávislé.
Nápověda 5
Nyní už stačí jen dosadit do vzorce (*) pro zobecněný princip virtuální práce:
\[\sum_{i=1}^{N} \vec{F}_i \cdot \delta \vec{r}_i = 0\ .\tag{*}\]Částici zkoumáme jen jedinou, takže znaménko sumy vlastně nebudeme potřebovat. Ze vzorce vhodně vyjádříme parametr α, čímž dostaneme podmínku, kterou musí splňovat rovnovážná poloha závaží.
Řešení
Kyvadlo má pouze jeden stupeň volnosti (komentář viz nápovědy výše). K jeho popisu tedy stačí jediný parametr. Za něj zvolíme výchylku kyvadla z rovnovážné polohy α.

Souřadnice vyjádříme vzhledem k parametru α a určíme složky vektoru nekonečně malých posunutí:
\[x = l \sin \alpha\] \[y = l \cos \alpha\]a určíme složky vektoru nekonečně malých posunutí:
\[\mathrm{d}x = l \cos \alpha \ \mathrm{d} \alpha\] \[\mathrm{d}y = -l \sin \alpha \ \mathrm{d} \alpha \ .\]Zapíšeme aktivní síly jako vektory:
\[\vec{F}_g = (0,\ mg)\ ,\] \[\vec{F}_e = (qE,\ 0)\ .\]Jejich výslednicí tedy je:
\[\vec{F} = (qE,\ mg)\ .\]Tu dosadíme do zobecněného principu virtuální práce:
\[\sum_{i=1}^{N} \vec{F}_i \cdot \delta \vec{r}_i = 0\ .\]V našem případě máme jen jeden hmotný bod, proto:
\[(qE,\ mg) \cdot \delta \vec{r} = 0\ .\]Po dosazení dostáváme:
\[(qE,\ mg) \cdot (l \cos \alpha \ \mathrm{d}\alpha,\ -l \sin \alpha \mathrm{d}\alpha) = 0\ .\]Vynásobíme a upravíme:
\[qEl \cos \alpha \ \mathrm{d}\alpha - mgl \sin \alpha \ \mathrm{d}\alpha = 0\] \[mg \sin \alpha = qE \cos \alpha\] \[\tan \alpha = \frac{qE}{mg}\ .\]Takové hodnoty α budou existovat dvě. Stabilní rovnovážná poloha, která je přibližně naznačena na všech náčrtcích a labilní poloha, kterou by kulička zaujala při výchylce vzdálené od stabilní polohy o 180° (tj. vzhledem k náčrtku by existovala „nad stropem“).
Odpověď
Kyvadlo je v rovnovážné poloze, jestliže pro jeho výchylku z rovnovážné polohy α platí:
\[\tan \alpha = \frac{qE}{mg}\ .\]Takové hodnoty α budou existovat dvě. Stabilní rovnovážná poloha, která je přibližně naznačena na všech náčrtcích a labilní poloha, kterou by kulička zaujala při výchylce vzdálené od stabilní polohy o 180° (tj. vzhledem k náčrtku by existovala „nad stropem“).
Komentář – princip virtuální práce versus klasické newtonovské řešení
Je zřejmé, že ke stejnému výsledku bychom došli pomocí „newtonovských“ postupů.
Pokud si kuličku představíme jako hmotný bod na tyčce zanedbatelné hmotnosti, tj. bod může konat pouze otáčivý pohyb po kružnici se středem v bodě pevného uchycení závěsu, pak stačí, když jeho rovnovážná poloha bude splňovat podmínku:
\[\vec{M}_e + \vec{M}_g = 0,\]kde \(\vec{M}\) jsou momenty příslušných sil vzhledem k bodu uchycení závěsu.
Odtud z geometrie experimentu a dosazení za velikosti sil dostaneme:
\[qEl \cos \alpha - mgl \sin \alpha = 0.\]Úpravou tohoto vztahu dojdeme ke stejnému řešení jako pomocí zobecněného principu virtuální práce:
\[\tan \alpha = \frac{qE}{mg}.\]


