Malé kmity spřažených kyvadel stejné hmotnosti
Úloha číslo: 2268
Mějme dvě matematická kyvadla hmotnosti \(m\) na tuhém závěsu délky \(l\). Kyvadla jsou zavěšena vedle sebe ve stejné výšce ve vzdálenosti \(d\). Kyvadla jsou spolu ve vzdálenosti \(\frac{l}{2}\) od místa zavěšení spojena pružinou tuhosti \(k\) o klidové délce \(d\).
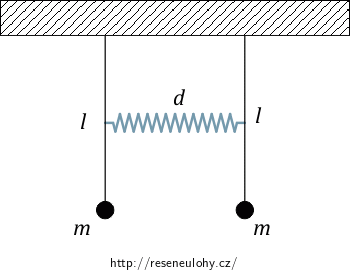
Určete pohybové rovnice pro tuto soustavu. Potenciální energii aproximujte pomocí teorie malých kmitů.
Nápověda 1
Najděte soustavu souřadnic vhodnou pro popis našeho problému.
Vyberte, s jakými zobecněnými souřadnicemi budete chtít pracovat.
Vyjádřete polohu a rychlost jednotlivých kyvadel.
Nápověda 2
Najděte lagrangián \(L\). Pro zjednodušení potenciální energie použijte kvadratickou aproximaci.
Nápověda 3
Použijte Lagrangeovy rovnice druhého druhu. Najděte pohybové rovnice platné pro naši soustavu.
Celkové řešení
Zvolme soustavu souřadnic s počátkem v bodě zavěšení prvního kyvadla, jejíž osa \(x\) směřuje k bodu zavěšení druhého kyvadla a osa \(y\) je svislá.
Za zobecněné souřadnice budeme brát úhly \(\varphi_1\) a \(\varphi_2\) odklonu od svislého směru jednotlivých kyvadel tak, jak je zobrazeno na obrázku.
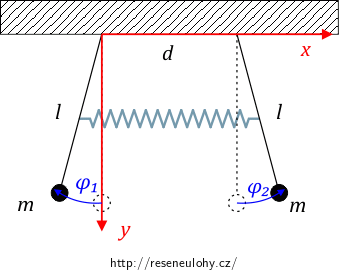
Pomocí goniometrických funkcí určíme souřadnice obou kyvadel.
\[\begin {matrix} x_1 = - l \sin \varphi_1 & & & & x_2 = l \sin \varphi_2 + d \\ y_1 = l \cos \varphi_1 & & & & y_2 = l \cos \varphi_2 \end {matrix}\]Rychlosti kyvadel \(\vec v_1\) a \(\vec v_2\) již určíme snadno.
\[\vec v_1 = \left( - l \cos \varphi_1 \cdot \dot \varphi_1 \, ; - l \sin \varphi_1 \cdot \dot \varphi_1 \right)\] \[\vec v_2 = \left( l \cos \varphi_2 \cdot \dot \varphi_2 \, ; - l \sin \varphi_2 \cdot \dot \varphi_2 \right)\]K určení lagrangiánu \(L = T - V\) budeme potřebovat znát vztahy pro kinetickou energii \(T\) a potenciální energii \(V\). Kinetickou energii určíme podle dobře známého vztahu \(T = \frac{1}{2} \sum_i m_i v_i^2\).
\[T = \frac{1}{2} m v_1^2 + \frac{1}{2} m v_2^2 = \] \[= \frac{1}{2} m \left[ l^2 \cos^2 \varphi_1 \cdot \dot \varphi_1^2 + l^2 \sin^2 \varphi_1 \cdot \dot \varphi_1^2 + l^2 \cos^2 \varphi_2 \cdot \dot \varphi_2^2 + l^2 \sin^2 \varphi_2 \cdot \dot \varphi_2^2 \right]\] \[T = \frac{1}{2} m l^2 \left( \dot \varphi_1^2 + \dot \varphi_2^2 \right)\]Do potenciální energie musíme zahrnout jak tíhovou potenciální energii \(V_t\), tak potenciální energii pružiny \(V_p\).
\[V = V_t + V_p\]Pro tíhovou potenciální energii \(V_t\) bude platit:
\[V_t = - m g y_1 - m g y_2 \, .\] \[V_t = - m g l \left( \cos \varphi_1 + \cos \varphi_2 \right)\]Pro potenciální energii pružiny \(V_p\) platí:
\[V_p = \frac{1}{2} k \, \Delta d^2 \, ,\]kde \(\Delta d\) je prodloužení pružiny. V našem případě bude platit následující vztah.
\[V_p = \frac{1}{2} k \left( \frac{l}{2} \sin \varphi_1 + \frac{l}{2} \sin \varphi_2 + d - d \right)^2\] \[V_p = \frac{k l^2}{8} \left( \sin \varphi_1 + \sin \varphi_2 \right)^2\]Tedy celková potenciální energie \(V\) bude mít tvar:
\[V = - m g l \left( \cos \varphi_1 + \cos \varphi_2 \right) + \frac{k l^2}{8} \left( \sin \varphi_1 + \sin \varphi_2 \right)^2\]Jelikož nás zajímají pouze malé kmity v okolí rovnovážné polohy, budeme chtít potenciál aproximovat kvadratickou funkcí \(\varphi\).
Z Maclaurinových řad funkcí \(\sin \varphi\) a \(\cos \varphi\) získáme hledanou aproximaci vcelku snadno.
\[\sin \varphi \approx \varphi\] \[\cos \varphi \approx 1 - \frac{\varphi^2}{2}\]Tedy se nám předpis pro potenciální energii \(V\) zjednodušší na:
\[V = - m g l \left( 2 - \frac{\varphi_1^2 + \varphi_2^2}{2} \right) + \frac{k l^2}{8} \left( \varphi_1 + \varphi_2 \right)^2 \, .\]A pro lagrangián \(L\) dostáváme:
\[L = \frac{1}{2} m l^2 \left( \dot \varphi_1^2 + \dot \varphi_2^2 \right) + m g l \left( 2 - \frac{\varphi_1^2 + \varphi_2^2}{2} \right) - \frac{k l^2}{8} \left( \varphi_1 + \varphi_2 \right)^2 \, .\]Použijeme Lagrangeovy rovnice druhého druhu.
\[\frac{\partial}{\partial t} \left( \frac{\partial L}{\partial \dot{\varphi_i}} \right) - \frac{\partial L}{\partial \varphi_i} = 0\]Teď si spočítáme všechny potřebné derivace.
\[\frac{\partial L}{\partial \dot{\varphi_1}} = m l^2 \dot \varphi_1\] \[\frac{\partial L}{\partial \dot{\varphi_2}} = m l^2 \dot \varphi_2\] \[\frac{\partial L}{\partial \varphi_1} = - m g l \varphi_1 - \frac{k l^2}{4} \left( \varphi_1 + \varphi_2 \right)\] \[\frac{\partial L}{\partial \varphi_2} = - m g l \varphi_2 - \frac{k l^2}{4} \left( \varphi_1 + \varphi_2 \right)\]Nyní dosaďme do Lagrangeových rovnic a dostaneme pohybové rovnice pro jednotlivá kyvadla.
\[m l^2 \ddot \varphi_1 + m g l \varphi_1 + \frac{k l^2}{4} \left( \varphi_1 + \varphi_2 \right) = 0\] \[m l^2 \ddot \varphi_2 + m g l \varphi_2 + \frac{k l^2}{4} \left( \varphi_1 + \varphi_2 \right) = 0\]Přesně jak bychom očekávali, lze vidět, že pohyb jednoho kyvadla je skrze tuhost pružiny svázán s pohybem druhého.
\[\ddot \varphi_1 + \frac{g}{l} \varphi_1 + \frac{k}{4 m} \left( \varphi_1 + \varphi_2 \right) = 0\tag{1}\] \[\ddot \varphi_2 + \frac{g}{l} \varphi_2 + \frac{k}{4 m} \left( \varphi_1 + \varphi_2 \right) = 0\tag{2}\]Odečtením rovnice (2) od rovnice (1) dostaneme rovnici:
\[\ddot \varphi_1 - \ddot \varphi_2 + \frac{g}{l} \left( \varphi_1 - \varphi_2 \right)= 0\tag{3}\]Označíme-li \(a = \varphi_1 - \varphi_2\), pak pro \(a\) máme rovnici:
\[\ddot a + \frac{g}{l} a = 0 \, .\]Tato rovnice odpovídá harmonickému kmitání s úhlovou frekvencí \(\sqrt \frac{g}{l}\), tedy s frekvencí, jaká odpovídá vlastní frekvenci oscilátoru bez spřažení.
\(a\) popisuje kmitání obou kyvadel společně, neboli celá soustava kmitá podle rovnice (3) s frekvencí \(\sqrt \frac{g}{l}\).
Sečteme-li rovnice (1) a (2), získáme:
\[\ddot \varphi_1 + \ddot \varphi_2 + \frac{g}{l} \left( \varphi_1 + \varphi_2 \right) + \frac{k}{2 m} \left( \varphi_1 + \varphi_2 \right) = 0\tag{4}\]Označíme-li tentokrát \(b = \varphi_1 + \varphi_2\), bude pro \(b\) platit následující rovnice.
\[\ddot b + \left(\frac{g}{l} + \frac{k}{2 m} \right) b = 0\]To odpovídá kmitání o úhlové frekvenci \(\sqrt {\frac{g}{l} + \frac{k}{2 m}}\). Vidíme, že tato frekvence je nutně větší než frekvence kmitání \(a\). Díky působení vazby tedy budou kyvadla kmitat s větší úhlovou frekvencí.
\(b\) popisuje, jak kmitají kyvadla proti sobě.
Tato dvě řešení pro \(a\) a pro \(b\) jsou na sobě nezávislá a nazývají se módy kmitání. Skutečně obecné řešení dostaneme lineární kombinací módů kmitání.
Odpověď
Pro potenciální energii \(V\) platí vztah:
\[V = - m g l \left( \cos \varphi_1 + \cos \varphi_2 \right) + \frac{k l^2}{8} \left( \sin \varphi_1 + \sin \varphi_2 \right)^2 \, .\]Užijeme-li pro potenciální energii aproximace
\[V = - m g l \left( 2 - \frac{\varphi_1^2 + \varphi_2^2}{2} \right) + \frac{k l^2}{8} \left( \varphi_1 + \varphi_2 \right)^2 \, ,\]budou mít pohybové rovnice pro naše kyvadla následující tvar.
\[\ddot \varphi_1 + \frac{g}{l} \varphi_1 + \frac{k}{4 m} \left( \varphi_1 + \varphi_2 \right) = 0\] \[\ddot \varphi_2 + \frac{g}{l} \varphi_2 + \frac{k}{4 m} \left( \varphi_1 + \varphi_2 \right) = 0\]

