Matematické kyvadlo

Úloha číslo: 669

Napište lagrangián rovinného matematického kyvadla (hmotného bodu o hmotnosti m na nehmotném závěsu délky l; druhý konec závěsu je pevně kotven).

Sestavte a vyřešte Lagrangeovu rovnici II. druhu pro malé kmity kyvadla.

Nápověda 1
Kolik má systém stupňů volnosti? Jaké zobecněné souřadnice zvolíme?

Všimněte si, že zadání říká, že kyvadlo se může pohybovat pouze v rovině.
Řešení nápovědy 1
Soustava má jeden stupeň volnosti, takže k jejímu popisu bude stačit jen jedna zobecněná souřadnice.

Zvolíme okamžitou výchylku kyvadla z rovnovážné polohy φ.
Nápověda 2
Nyní budeme potřebovat vyjádřit kinetickou a potenciální energii pomocí souřadnice φ.

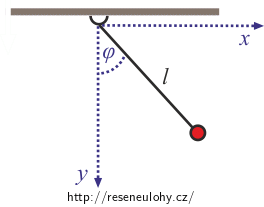
Zkuste k vyjádření potenciální energie nejprve použít kartézskou souřadnici y, která má svislý směr a počátek v místě uchycení závěsu kyvadla. Vyjádřete souřadnici y pomocí zobecněné souřadnice φ.
Řešení nápovědy 2
Potenciální energii můžeme pomocí souřadnice y psát:
\[V\left(y\right) = -mgy\ .\]
Z geometrie experimentu zjevně platí:
\[y = l\cos \varphi\ .\]
Odtud pro potenciální energii pomocí souřadnice φ dostáváme:
\[V\left(\varphi\right) = -mgl\cos \varphi\ .\]
Nápověda 3
Pohyb kyvadla je pohybem hmotného bodu po kružnici o poloměru l. Jak spočteme jeho kinetickou energii?
Řešení nápovědy 3
Kinetická energie hmotného bodu se dá psát podle známého vzorce:
\[T = \frac{1}{2}mv^2\ .\]
Obvodovou rychlost v pohybu po kružnici o poloměru r při znalosti úhlové rychlosti ω vyjádříme:
\[v = \omega r\ .\]
Odtud je kinetická energie pohybu hmotného bodu po kružnici:
\[T = \frac{1}{2}mr^2\omega^2\ .\]
Za poloměr kružnice r dosadíme délku kyvadla l a za úhlovou rychlost ω první časovou derivaci okamžité výchylky φ:
\[T \left(\varphi\right) = \frac{1}{2}ml^2\dot{\varphi}^2\ .\]
Nápověda 4
Lagrangeova funkce L má tvar:
\[L = T-V\ .\]
Řešení – lagrangián
Systém má jeden stupeň volnosti, k jeho popisu tedy stačí jedna souřadnice. Za ní zvolíme okamžitou výchylku kyvadla φ.

Z obrázku je jasné, že pro potenciální energii můžeme psát:
\[V\left(y\right)= -mgy\ .\]
Z geometrie experimentu vyplývá:
\[y = l\cos \varphi\]
a tedy:
\[V\left(\varphi\right) = -mgl\cos\varphi\ .\]
Kinetická energie pohybu hmotného bodu po kružnici se dá zapsat:
\[T = \frac{1}{2}mr^2\omega^2\ .\]
V našem případě platí:
\[r = l\] \[\omega = \dot {\varphi}\ ,\]
takže můžeme psát:
\[T \left(\varphi\right) = \frac{1}{2}ml^2\dot{\varphi}^2\ .\]
Lagrangeova funkce (lagrangián) má obecný předpis:
\[L = T-V\ .\]
Po dosazení výše určených energií:
\[L = \frac{1}{2}ml^2\dot{\varphi}^2 + mgl\cos\varphi\ .\]
Nápověda 5
Obecný tvar Lagrangeových rovnic II. druhu je:

\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\ ,\] pro j = 1, 2 ... n,

kde q_j je j-tá zobecněná souřadnice hmotného bodu a L Lagrangeova funkce.

V naší úloze máme jen jednu zobecněnou souřadnici φ, proto budeme mít jen jednu Lagrangeovu rovnici.

Sestavte Lagrangeovu rovnici II. druhu matematického kyvadla.
Řešení nápovědy 5
Tvar rovnice pro náš případ bude:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\varphi}}\right)-\frac{\partial L}{\partial \varphi} = 0\ .\]
Připravíme si derivace lagrangiánu:
\[\frac{\partial L}{\partial \dot{\varphi}} = ml^2\dot{\varphi}\] \[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{\varphi}} = ml^2\ddot{\varphi}\] \[\frac{\partial L}{\partial \varphi}=-mgl\sin \varphi\,.\]
Lagrangeova rovnice II. druhu má tedy tvar:
\[ml^2\ddot{\varphi} + mgl\sin \varphi = 0\]
a po úpravě:
\[\ddot{\varphi} + \frac{g}{l}\sin \varphi = 0\ .\]
Nápověda 6
Řešení Lagrangeovy rovnice, kterou jsme získali v předchozím oddíle, je analyticky velmi komplikované. Protože nás ale zajímají malé kmity tohoto kyvadla, tj. řešení pro malá φ, zkusme ji linearizovat, tedy zbavit se funkce sinus, která v ní vystupuje.

Je potřeba udělat Taylorův rozvoj sinu v bodě nula (McLaurinův rozvoj).
Řešení nápovědy 6
Z Taylorova rozvoje funkce sinus v okolí nuly dostáváme:
\[ \sin \varphi = \varphi - \frac{1}{6}\varphi^3 + \frac{1}{120}\varphi^5 + ...\ .\]
Průběh funkce sinus je v okolí nuly téměř lineární. Použijeme tedy aproximaci:
\[\sin \varphi \approx \varphi\ .\]
Dosazením dostáváme lineární diferenciální rovnici:
\[\ddot{\varphi} + \frac{g}{l} \varphi = 0\ ,\]
tedy rovnici pro lienární harmonický oscilátor, kterou je již velmi jednoduché vyřešit.
Řešení – úprava rovnice pro malé kmity a kroky v jejím řešení
Z lagrangiánu jsme podle předpisu Lagrangeových rovnic II. druhu dospěli ke vztahu:
\[\ddot{\varphi}+\frac{g}{l}\sin\varphi = 0\ .\]
Pro malé výchylky můžeme použít přibližný vzorec:
\[\sin \varphi \approx \varphi\ ,\]
který dostaneme například pomocí Taylorova rozvoje kolem nuly.

Odtud tedy:
\[\ddot{\varphi}+\frac{g}{l}\varphi = 0\ ,\]
což je rovnice lineárního harmonického oscilátoru s řešením:
\[\varphi = A\sin \left(\sqrt{\frac{g}{l}}t+ \varphi_0\right)\ ,\]
kde A je amplituda kmitů kyvadla a φ₀ počáteční výchylka.

Pro peridou kmitů platí:
\[T = \frac{1}{f} = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{l}{g}}\ .\]
Odpověď
Lagrangián rovinného matematického kyvadla je:
\[L = \frac{1}{2}ml^2\dot{\varphi}^2 + mgl\cos\varphi\ ,\]
kde φ je výchylka z rovnovážné polohy.

Řešením linearizované pohybové rovnice dostáváme:
\[\varphi = A\sin \left( \sqrt{\frac{g}{l}}t+ \varphi_0\right)\ ,\]
kde A je amplituda výchylky kmitání a φ₀ počáteční fáze.
Přesné řešení aneb malý hodinářský komentář
Jak by vypadalo řešení bez linearizace rovnice? Co se děje při větších výchylkách?

Z řešení snadno určíme, že perioda T kmitu matematického kyvadla pro malé výchylky je:
\[T = 2\pi \sqrt{\frac{l}{g}}\ .\]
Řešení nelinearizované pohybové rovnice je poměrně složité. Odvození přesného vztahu pro periodu kmitů si můžete prohlédnout například zde: Přesné řešení matematického kyvadla .

Pro nás je důležitý tento závěr:

Perioda kmitu matematického kyvadla bez přiblížení pro malé kmity není konstantní, ale je funkcí počáteční výchylky φ₀, kterou dostaneme jako součet řady:
\[T\left(\varphi_0\right) = 2\pi\sqrt{\frac{l}{g}}\left(1+\frac{1}{4}\sin^2\frac{\varphi_0}{2} + \frac{9}{64}\sin^4\frac{\varphi_0}{2} + \frac{25}{256}\sin^6\frac{\varphi_0}{2}+...\right)\ .\]
Matematické kyvadlo tedy nekoná izochronní kmity (jeho perioda kmitu není konstantní).

Z „hodinářského“ hlediska to znamená, že kyvadlo kyvadlových hodin se musí kývat s konstantní amplitudou – a nastavením délky kyvadla se musí upravit jeho perioda, aby hodiny šly přesně. Existují ovšem i kyvadla konající izochronní kmity, například kyvadlo cykloidální.