Řetězovka

Úloha číslo: 1056

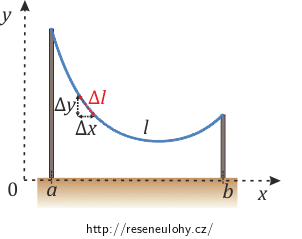
Necháme-li volně viset dokonale ohebný, neprotažitelný a homogenní provaz, ukotvený ve dvou bodech, zaujme tvar křivky, kterou nazýváme řetězovka. Určete analytické vyjádření této křivky.

Nápověda 1 – co určuje tvar křivky

Každý fyzikální systém se snaží zaujmout stav s nejmenší možnou energií. Tvar křivky \(y=y(x)\), kterou provaz zaujme, určuje tedy minimum potenciální energie.

Pokuste se vyjádřit potenciální energii nejprve malého kousku provazu pomocí jeho délky a polohy a poté tyto příspěvky „posčítejte“.
Řešení nápovědy 1

Nejprve vyjádřeme délku malého kousku provazu. Díváme-li se dostatečně zblízka, můžeme daný kousek považovat za úsečku, a tedy píšeme:
\[\Delta l=\sqrt{(\Delta x)^2+(\Delta y)^2}=\sqrt{(\Delta x)^2+(y^\prime\Delta x)^2}=\sqrt{1+(y^\prime )^2}\Delta x,\]
kde:
\[y^\prime=\frac{\mathrm{d}y}{\mathrm{d}x}\dot{=}\frac{\Delta y}{\Delta x}.\]
Napišme ještě element hmotnosti Δm:
\[\Delta m=\eta\Delta l=\eta \sqrt{1+(y^\prime)^2}\Delta x\]
a z toho plynoucí element potenciální energie ΔV:
\[\Delta V=\Delta mgy=\eta gy \sqrt{1+(y^\prime)^2}\Delta x,\]
kde η je lineární hustota provazu.

K celkové potenciální energii se dostaneme integrací přes x:
\[V=\eta g \int_a^b y \sqrt{1+(y^\prime)^2}\mathrm{d}x.\tag{1}\]
Nápověda 2 – další podmínky
Při řešení je třeba zohlednit skutečnost, že délka provazu je konstantní (viz zadání – provaz se nemůže protáhnout). Vyjádřete délku křivky, kterou provaz zaujal.
Řešení nápovědy 2 – další podmínky
Podmínku konstantní délky provazu vyjádříme integrálem:
\[l=\int_a^b \sqrt{1+(y^\prime)^2}\mathrm{d}x=\mathrm{konst}.\tag{2}\]
Nápověda 3 – sestavení funkcionálu
Pokud provaz zaujme nejvýhodnější polohu, má minimální potenciální energii V a tedy variace potenciální energie je rovna nule, tj.:
\[\delta V=0.\]
Délka provazu l je konstantní, tj. i její variace je nulová:
\[\delta l=0.\]
Obě tyto podmínky můžeme spojit v jedinou (jedná se vlastně o použití metody Lagrangeových multiplikátorů) ve tvaru:
\[\delta V-\lambda\delta l=0,\]
kde o multiplikátoru λ budeme předpokládat, že nezávisí na souřadnicích.

Napište funkcionál, který odpovídá této podmínce.
Řešení nápovědy 3 – sestavení funkcionálu
Upravíme podmínku z nápovědy na tvar:
\[\delta(V-\lambda l)=0,\]
kde v závorce je hledaný funkcionál F, jehož minimum hledáme.

Dosadíme a upravíme:
\[F=\int_a^b\left(\eta gy \sqrt{1+(y^\prime)^2}-\lambda \sqrt{1+(y^\prime)^2}\right)\mathrm{d}x=\int_a^b(\eta gy-\lambda)\sqrt{1+(y^\prime)^2}\,\mathrm{d}x.\]
Nápověda 4
V předchozí nápovědě jsme našli funkcionál, můžeme sestavit příslušnou Eulerovu-Lagrangeovu rovnici a tu vyřešit.

Eulerova-Lagrangeova rovnice má obecně tvar:
\[\frac{\partial{F}}{\partial{y}}-\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{F}{y^\prime}\right)=0.\]
Využijte také skutečnosti, že funkcionál F není explicitně závislý na proměnné x.
Řešení nápovědy 4 – nalezení diferenciální rovnice
Funkcionál F má stacionární hodnotu, pokud je splněna Eulerova-Lagrangeova rovnice. Ta v našem případě nabývá tvaru:
\[\frac{\partial{F}}{\partial{y}}-\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{F}{y^\prime}\right)=0.\]
Mohli bychom již teď dosadit konkrétní tvar funkcionálu F a získanou rovnici řešit. Výhodnější je ale využít skutečnosti, že funkcionál F není explicitně závislý na proměnné x. V takovém případě můžeme Eulerovu-Lagrangeovu rovnici převést do příjemnějšího tvaru následujícími úpravami.

Nejprve vynásobíme rovnici \(y^\prime\):
\[y^\prime\frac{\partial{F}}{\partial{y}}-y^\prime\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{F}{y^\prime}\right)=0.\]
Rovnici můžeme podle pravidel pro derivování funkce více proměnných (funkcionál F je funkcí dvou proměnných \(F=F(y,y^\prime)\) ) psát ve tvaru:
\[\frac{\mathrm{d}F}{\mathrm{d}x}-y^{\prime\prime}\frac{\partial{F}}{\partial{y^\prime}}-\frac{\mathrm{d}}{\mathrm{d}x}\left(y^\prime\frac{\partial{F}}{\partial{y^\prime}}\right)+\frac{\partial{F}}{\partial{y^\prime}}y^{\prime\prime}=0.\]
Všimneme si, že druhý a čtvrtý člen se odečtou, zbylé členy dáme pod společnou derivaci a můžeme tak psát:
\[\frac{\mathrm{d}}{\mathrm{d}x}\left(F-y^\prime\frac{\partial{F}}{\partial{y^\prime}}\right)=0,\]
rovnici zintegrujeme podle proměnné x a dostáváme tak vztah:
\[F-y^\prime\frac{\partial{F}}{\partial{y^\prime}}=c,\]
kde c je integrační konstanta.

Dosazením konkrétního tvaru funkcionálu F získáme:
\[c=(y-\lambda)\sqrt{1+(y^\prime)^2}-y^\prime\frac{\partial}{\partial y^\prime}\left[(y-\lambda)\sqrt{1+(y^\prime)^2}\right].\]
V rovnici jsme kvůli přehlednosti vynechali u y koeficient ηg. Jelikož je tento koeficient konstantní a nenulový, mohli bychom s ním rovnici vydělit a zahrnout jej do konstanty c a variačního koeficientu λ, na které jsme zatím nekladli žádné požadavky.

Provedeme naznačenou derivaci a pravou stranu upravíme:
\[c=(y-\lambda)\left[\sqrt{1+(y^\prime)^2}-\frac{2y^\prime y^\prime}{2\sqrt{1+(y^\prime)^2}}\right]=(y-\lambda) \frac{1}{\sqrt{1+(y^\prime)^2}}.\]
Nalezli jsme tedy diferenciální rovnici:
\[c=(y-\lambda) \frac{1}{\sqrt{1+(y^\prime)^2}},\]
kterou je třeba vyřešit.
Užitečný integrál
K řešení diferenciální rovnice se vám může hodit znalost integrálu:
\[\int{\frac{\mathrm{d}u}{\sqrt{u^2-a^2}}}= \mathrm{argcosh}\, {\left(\frac{u}{a}\right)}+c.\]
Řešení nápovědy 4 – řešení diferenciální rovnice
Diferenciální rovnici přepišme do tvaru
\[c\sqrt{1+(y^\prime)^2}=y-\lambda.\]
K řešení použijeme seperaci proměnných.

Nejprve rovnici umocníme na druhou:
\[c^2+c^2(y^\prime)^2=(y-\lambda)^2.\]
První člen převedeme na pravou stranu a \(y^\prime\) přepíšeme pomocí diferenciálů:
\[c^2\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^2=(y-\lambda)^2-c^2.\]
Nyní provedem samotnou separaci – rovnici upravíme tak, aby vlevo byla pouze souřadnice y společně se svým diferenciálem \(\mathrm{d}y\) a vpravo to samé v proměnné x:
\[\frac{c^2}{(y-\lambda)^2-c^2}\mathrm{d}y^2=\mathrm{d}x^2.\]
Rovnici odmocníme:
\[\frac{c}{\sqrt{(y-\lambda)^2-c^2}}\mathrm{d}y=\mathrm{d}x\]
a obě strany rovnice zintegrujeme podle příslušných proměnných (pro integraci výrazu na levé straně využijte znalost integrálu v nápovědě před tímto oddílem):
\[c\ \mathrm{argcosh}\,{\left(\frac{y-\lambda}{c}\right)}+c_1=x+c_2.\]
Zavedeme jedinou integrační konstantu C vztahem \(C=c_2-c_1\) a po úpravě dostáváme rovnici do tvaru:
\[\mathrm{argcosh}\,{\left(\frac{y-\lambda}{c}\right)}=\frac{x+C}{c}.\]
Na celou rovnost použijeme funkci cosh a získáme tak:
\[y-\lambda=c\,\cosh{\left(\frac{x+C}{c}\right)},\]
ze které již snadno vyjádříme hledanou závislost souřadnice y a tedy i tvar křivky řetězovky jako:
\[y=\lambda+c\,\cosh{\left(\frac{x+C}{c}\right)}.\]
Celkové řešení
Vyjádřeme malý kousek řetězovky. Díváme-li se dostatečně zblízka, můžeme daný kousek považovat za úsečku, a tedy psát:
\[\Delta l=\sqrt{(\Delta x)^2+(\Delta y)^2}=\sqrt{(\Delta x)^2+(y^\prime\Delta x)^2}=\sqrt{1+(y^\prime )^2}\Delta x,\]
kde \[y^\prime=\frac{\Delta y}{\Delta x}\dot{=}\frac{\mathrm{d}y}{\mathrm{d}x}.\]

Napišme ještě element hmotnosti Δm a z toho plynoucí element potenciální energie ΔV.
\[\Delta m=\eta\Delta l=\eta \sqrt{1+(y^\prime)^2}\Delta x,\] \[\Delta V=\Delta mgy=\eta gy \sqrt{1+(y^\prime)^2}\Delta x.\]
K celkové potenciální energii se dostaneme integrací přes všechna x:
\[V=\eta g \int_a^b y \sqrt{1+(y^\prime)^2}\mathrm{d}x.\]
Pro délku křivky l, která je konstantní, platí podmínka:
\[l=\int_a^b \sqrt{1+(y^\prime)^2}\mathrm{d}x=\mathrm{konst.}\]
Pokud provaz zaujme nejvýhodnější polohu, má minimum potenciální energie V, a tedy variace potenciální energie je rovna nule, tj.:
\[\delta V=0.\]
Délka provazu l je konstantní, tj. i její variace je nulová:
\[\delta l=0.\]
Obě tyto podmínky můžeme spojit v jedinou (jedná se vlastně o použití metody Lagrangeových multiplikátorů) ve tvaru:
\[\delta V-\lambda\delta l=0,\]
kde o multiplikátoru λ budeme předpokládat, že nezávisí na souřadnicích.

Podmínku upravíme na tvar:
\[\delta(V-\lambda l)=0,\]
kde v závorce je funkcionál F, jehož minimum hledáme.

Dosadíme a upravíme:
\[F=\int_a^b\left(\eta gy \sqrt{1+(y^\prime)^2}-\lambda \sqrt{1+(y^\prime)^2}\right)\mathrm{d}x=\int_a^b(\eta gy-\lambda)\sqrt{1+(y^\prime)^2}\mathrm{d}x.\]
Jelikož se nám povedlo nalézt funkcionál, můžeme začít řešit Eulerovu-Lagrangeovu rovnici, která má obecně tvar:
\[\frac{\partial{F}}{\partial{y}}-\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{F}{y^\prime}\right)=0.\]
S využitím skutečnosti, že funkcionál F není expilicitně závislý na proměnné x, můžeme Eulerovu-Lagrangeovu rovnici převést do tvaru:
\[\frac{\mathrm{d}}{\mathrm{d}x}\left(F-y^\prime\frac{\partial{F}}{\partial{y^\prime}}\right)=0,\]
rovnici zintegrujeme podle proměnné x a dostáváme tak vztah:
\[F-y^\prime\frac{\partial{F}}{\partial{y^\prime}}=c,\]
kde c je integrační konstanta.

Dosazením konkrétního tvaru funkcionálu F získáme:
\[c=(y-\lambda)\sqrt{1+(y^\prime)^2}-y^\prime\frac{\partial}{\partial y^\prime}\left[(y-\lambda)\sqrt{1+(y^\prime)^2}\right].\]
V rovnici jsme kvůli přehlednosti vynechali u y koeficient ηg. Jelikož je tento koeficient konstantní a nenulový, rovnici jsme jím vydělili a zahrnuli ho do konstanty c a λ, na které jsme zatím nekladli žádné požadavky.

Provedeme naznačenou derivaci a pravou stranu upravíme:
\[c=(y-\lambda)\left[\sqrt{1+(y^\prime)^2}-\frac{2y^\prime y^\prime}{2\sqrt{1+(y^\prime)^2}}\right]=(y-\lambda) \frac{1}{\sqrt{1+(y^\prime)^2}}.\]
Nalezli jsme tedy diferenciální rovnici:
\[c=(y-\lambda) \frac{1}{\sqrt{1+(y^\prime)^2}}.\]
Diferenciální rovnici přepišme do tvaru.
\[c\sqrt{1+(y^\prime)^2}=y-\lambda.\]
K jejímu řešení je vhodné užít metodu separace proměnných. Tou dospějeme k řešení ve tvaru (podrobné řešení diferenciální rovnice naleznete v řešení nápovědy 4):
\[y=\lambda+c\,\cosh{\left(\frac{x+C}{c}\right)},\]
kde C je integrační konstanta.

Získali jsme tak závislost souřadnice y a tedy i tvar křivky popisující řetězovku.
Odpověď
Provaz zaujme tvar daný křivkou:
\[y=\lambda+c\,\cosh{\left(\frac{x+C}{c}\right)}.\]
Řetězovka má tedy tvar funkce hyperbolický cosinus.

Hodnoty integračních konstant c a C závisejí na souřadnicích koncových bodů a celkové délce provazu.
Komentář - zajímavosti
Řetězovka má mnoho praktických aplikací například v architektuře, ať už se jedná o závěsné mosty, či samonosné klenby. Příkladem může být Gateway Arch v Saint Louis nebo střecha nádraží Keleti v Budapešti.

Řetězovka je křivkou s minimem potenciální energie. Toho lze využít i v případě, že chceme minimální rotační plochu. V učebnici teoretické mechaniky od autorů Brdičky a Hladíka se píše toto: „Rotací řetězovky vznikají tedy jediné minimální plochy, které jsou plochami rotačními. Nazývají se katenoidy. Z geometrického hlediska je katenoid plochou nulové střední křivosti, tj. v každém jejím bodě se poloměry křivosti dvou k sobě kolmých řezů liší jen znaménkem.“

Některé zdroje uvádějí, že se tvaru řetězovky využívá i při výrobě houslí.