Sbírka řešených úloh

Hmotný bod na nakloněné rovině

Úloha číslo: 632

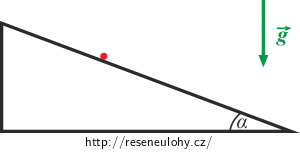
Hmotný bod o hmotnosti m se pohybuje bez tření po nakloněné rovině svírající s vodorovnou podložkou úhel α, gravitační zrychlení má velikost g a míří svisle dolů.

Hmotný bod se po nakloněné rovině pohybuje pouze nahoru nebo dolů (nemůže konat pohyb kolmý na nákresnu).

A) Napište Lagrangeovu funkci pohybu tohoto hmotného bodu
B) Sestavte a vyřešte Lagrangeovy rovnice II. druhu

• Nápověda 1

  Rozmyslete, kolik budeme potřebovat souřadnic k popisu tohoto pohybu. Kolik má soustava stupňů volnosti?

• Řešení nápovědy 1

  Hmotný bod se může pohybovat pouze nahoru a dolů po nakloněné rovině, soustava má tedy jediný stupeň volnosti, a k jejímu popisu proto musí stačit jediná zobecněná souřadnice.

• Nápověda 2

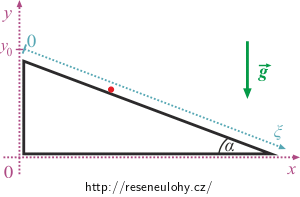
  Vyjádřete kinetickou a potenciální energii v kartézských souřadnicích (viz obrázek) a pak je přepište pomocí jediné souřadnice. Za tu zvolíme souřadnici ξ mířící dolů po povrchu nakloněné roviny.

  

• Řešení nápovědy 2

  Kinetickou a potenciální energii můžeme psát v kartézských souřadnicích:

  \[T = \frac{1}{2}m(\dot{x}^2 + \dot{y}^2)\] \[V = mgy + V_0\ ,\]

  kde V₀ je konstanta určující potenciální energii ve výšce y = 0.

  Z geometrie soustavy je zřejmé:

  \[x = \xi \cos \alpha\] \[y = -\xi \sin \alpha + y_0\ ,\]

  kde y₀ je konstanta vyjadřující posunutí počátku kartézské soustavy souřadnic vzhledem k počátku ξ.

  Pro kartézské složky rychlosti hmotného bodu platí:

  \[\dot{x} = \dot{\xi} \cos \alpha\] \[\dot{y} = -\dot{\xi} \sin \alpha\ ,\]

  tedy:

  \[\dot{x}^2 + \dot{y}^2 = \dot{\xi}^2\ .\]

  Odtud pro kinetickou a potenciální energii:

  \[T = \frac{1}{2}m\dot{\xi}^2\] \[V = -mg\xi \sin \alpha + V_0 + V'_0\ ,\]

  kde V'₀ je konstanta která musí být započtena vzhledem k posunutí počátků kartézské soustavy souřadnic a souřadnice ξ.

  Konstanty V₀ a V'₀ můžeme bez újmy na obecnosti (viz níže) sloučit a dále psát:

  \[V = -mg\xi \sin \alpha + \tilde{V}_0\ .\]

• Komentář

  Všimněte si, že vztahy spojující x, y a ξ jsou jednoznačné. Za zobecněnou souřadnici by tedy bylo možno vzít kteroukoli z nich (pokud je splněna podmínka, že úhel α není nulový, resp. pravý – pak by ξ splynula s osou x, resp. y.

  Pomocí výše uvedených vztahů bude taky možno vyjádřit výsledek vzhledem ke všem třem souřadnicícm.

  Je zde vidět výhoda lagrangeovských postupů: počítáme jen s tolika souřadnicemi, kolik nezbytně potřebujeme.

• Nápověda 3

  Lagrangeova funkce má tvar

  \[L = T - V \ ,\]

  kde T je kinetická a V potenciální energie. Napište, jak bude vypadat v našem případě.

• Řešení – Lagrangeova funkce

  Kinetickou a potenciální energii vyjádříme nejdříve v kartézských souřadnicích:

  \[T = \frac{1}{2}m(\dot{x}^2 + \dot{y}^2)\] \[V = mgy + V_0\]

  Vzhledem k tomu, že soustava má jen jeden stupeň volnosti, musí stačit k popisu pohybu hmotného bodu jen jedna souřadnice. Volíme souřadnici ξ mířící dolů po povrchu nakloněné roviny.

  

  \[x = \xi \cos \alpha\] \[y = -\xi \sin \alpha + y_0\]

  (Podrobněji v nápovědách, viz výše.)

  Obě energie vyjádříme vzhledem k ní:

  \[T = \frac{1}{2}m\dot{\xi}^2\] \[V = -mg\xi \sin \alpha + \tilde{V}_0\]

  a napíšeme Lagrangeovu funkci:

  \[L = T-V\] \[L = \frac{1}{2}m\dot{\xi}^2 + mg\xi \sin \alpha - \tilde{V}_0\ .\]

• Nápověda 4

  Lagrangeovy rovnice II. druhu mají tvar:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\] pro j = 1, 2 ... n

  kde q_j je j-tá zobecněná souřadnice hmotného bodu a L Lagrangeova funkce. Napište rovnice pro náš případ.

• Dosazení

  Máme pouze jedinou souřadnici, takže neobdržíme soustavu rovnic, ale pouze jedinou rovnici:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\xi}}\right)-\frac{\partial L}{\partial {\xi}} = 0\tag{*}\]

  Připravíme si derivace lagrangiánu:

  \[L = \frac{1}{2}m\dot{\xi}^2 + mg\xi\sin \alpha - \tilde{V}_0\] \[\frac{\partial}{\partial \dot{\xi}}\left(\frac{1}{2}m\dot{\xi}^2 + mg\xi\sin \alpha -\tilde{V}_0\right) = m\dot{\xi}\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\xi}}\right) = \frac{d}{dt}m\dot{\xi} = m\ddot{\xi}\] \[\frac{\partial}{\partial {\xi}}\left(\frac{1}{2}m\dot{\xi}^2 + mg\xi\sin \alpha-\tilde{V}_0\right)=mg\sin\alpha\]

  Po dosazení do Lagrangeovy rovnice (*):

  \[m\ddot{\xi}-mg\sin\alpha=0\] \[\ddot{\xi}=g\sin\alpha\]

  Je vidět, že se do rovnic nedostala konstanta V₀. To potvrzuje skutečnost známou už z newtonovské mechaniky, a sice, že nulovou hladinu potenciální energie můžeme volit libovolně. Podstatný je funkční průběh potenciálu, aditivní konstanty v lagrangiánu se do řešení nedostanou.

• Řešení rovnice

  Dospěli jsme ke vztahu:

  \[\ddot{\xi}=g\sin\alpha\ ,\]

  tj. druhá derivace ξ se rovná konstantě.

  Po dvojím zintegrování dostaneme:

  \[\xi(t) = \frac{1}{2}gt^2\sin\alpha + C_1 t + C_2\ .\]

  Konstanty C₁, C₂ musíme určit z počátečních podmínek. Označme v čase t = 0 rychlost hmotného bodu v₀ a polohu ξ₀.

  Odtud dostáváme rovnice:

  \[\xi(0) = C_2 = \xi_0\] \[v(0) = C_1 = v_0\]

  a z nich výsledný vztah:

  \[\xi(t) = \frac{1}{2}gt^2\sin\alpha + v_0 t + \xi_0\ .\]

• Řešení – Lagrangeova rovnice

  Lagrangeovy rovnice II. druhu mají tvar:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\] pro j = 1, 2 ... n

  kde q_j je j-tá zobecněná souřadnice hmotného bodu a L Lagrangeova funkce. Napište rovnice pro náš případ.

  Máme pouze jedinou souřadnici, takže neobdržíme soustavu rovnic, ale pouze jedinou rovnici:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\xi}}\right)-\frac{\partial L}{\partial {\xi}} = 0\tag{*}\] \[m\ddot{\xi}-mg\sin\alpha=0\] \[\ddot{\xi}=g\sin\alpha\ ,\]

  tj. druhá derivace ξ je rovna konstantě. Tento vztah stačí pouze dvakrát zinetgrovat. Označme v čase t = 0 rychlost hmotného bodu v₀ a polohu ξ₀. Odtud:

  \[\xi(t) = \frac{1}{2}gt^2\sin\alpha + v_0 t + \xi_0\ .\]

  (Podrobnější komentáře viz nápovědy).

• Odpověď

  Lagrangián pohybu hmotného bodu na nakloněné rovině je:

  \[L = \frac{1}{2}m\dot{\xi}^2 + mg\xi\sin \alpha - \tilde{V}_0\ .\]

  Pohyb hmotného bodu na nakloněné rovině popisuje rovnice:

  \[\xi(t) = \frac{1}{2}gt^2\sin\alpha + v_0 t + \xi_0\ ,\]

  kde ξ je souřadnice mířící dolů po povrchu nakloněné roviny.

  Vidíme, že se jedná o rovnoměrně zrychlený pohyb se zrychlením rovným g sin α, tj. průmětu tíhového zrychlení do směru nakloněné roviny. Tento výsledek odpovídá výsledku, který bychom získali řešením pomocí „newtonovských“ postupů.

• Komentář

  Je zřejmé, že stejné řešení bude platit vždy, když budeme moci považovat těleso na nakloněné rovině za hmotný bod klouzající bez tření (např. hranol, sáňky).

  Pokud budeme uvažovat těleso valící se, nikoli jen klouzající, budeme muset upravit předpis pro kinetickou energii. Více o tom v úlohách Válec na nakloněné rovině a Vozík na nakloněné rovině.